广度优先搜索在抓牛问题中的应用

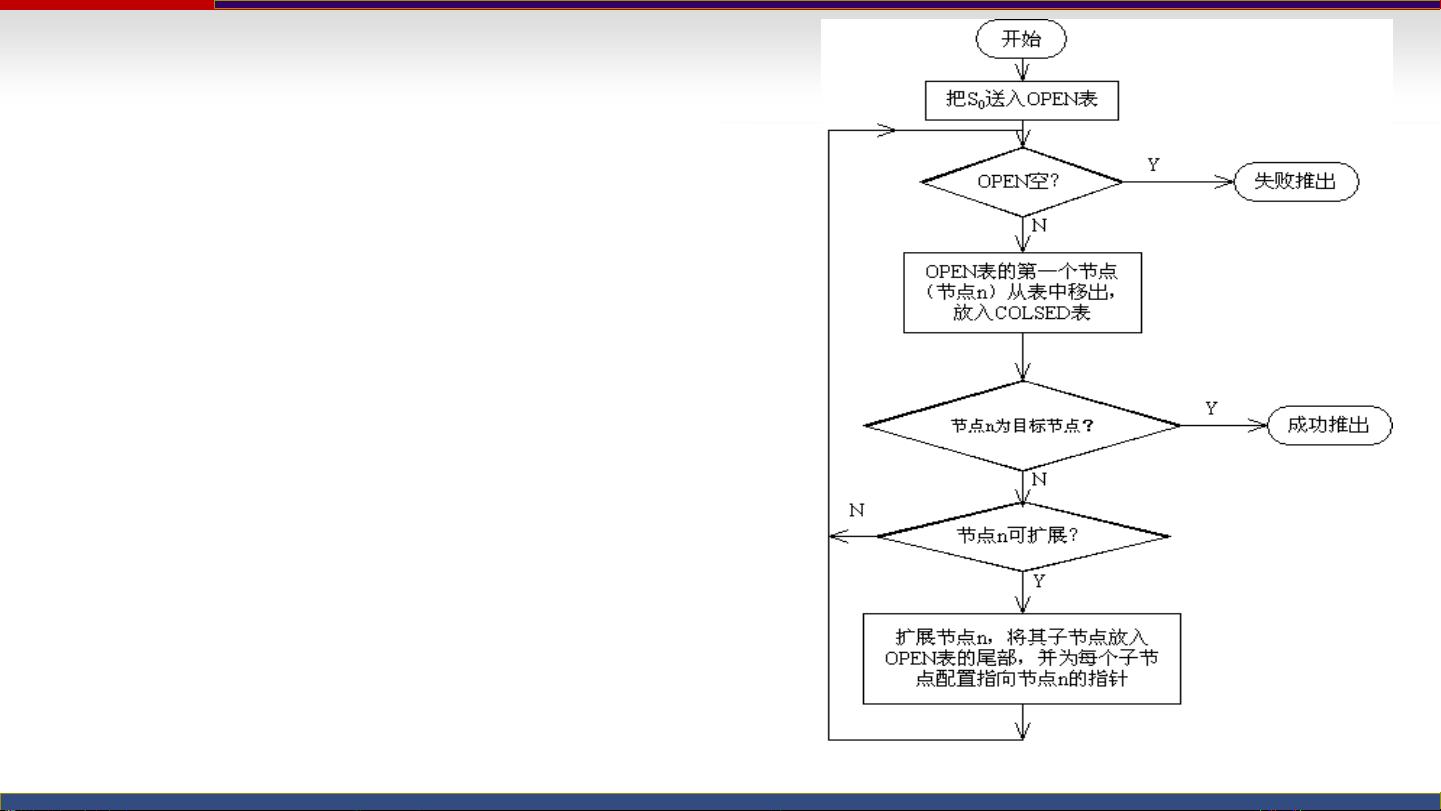
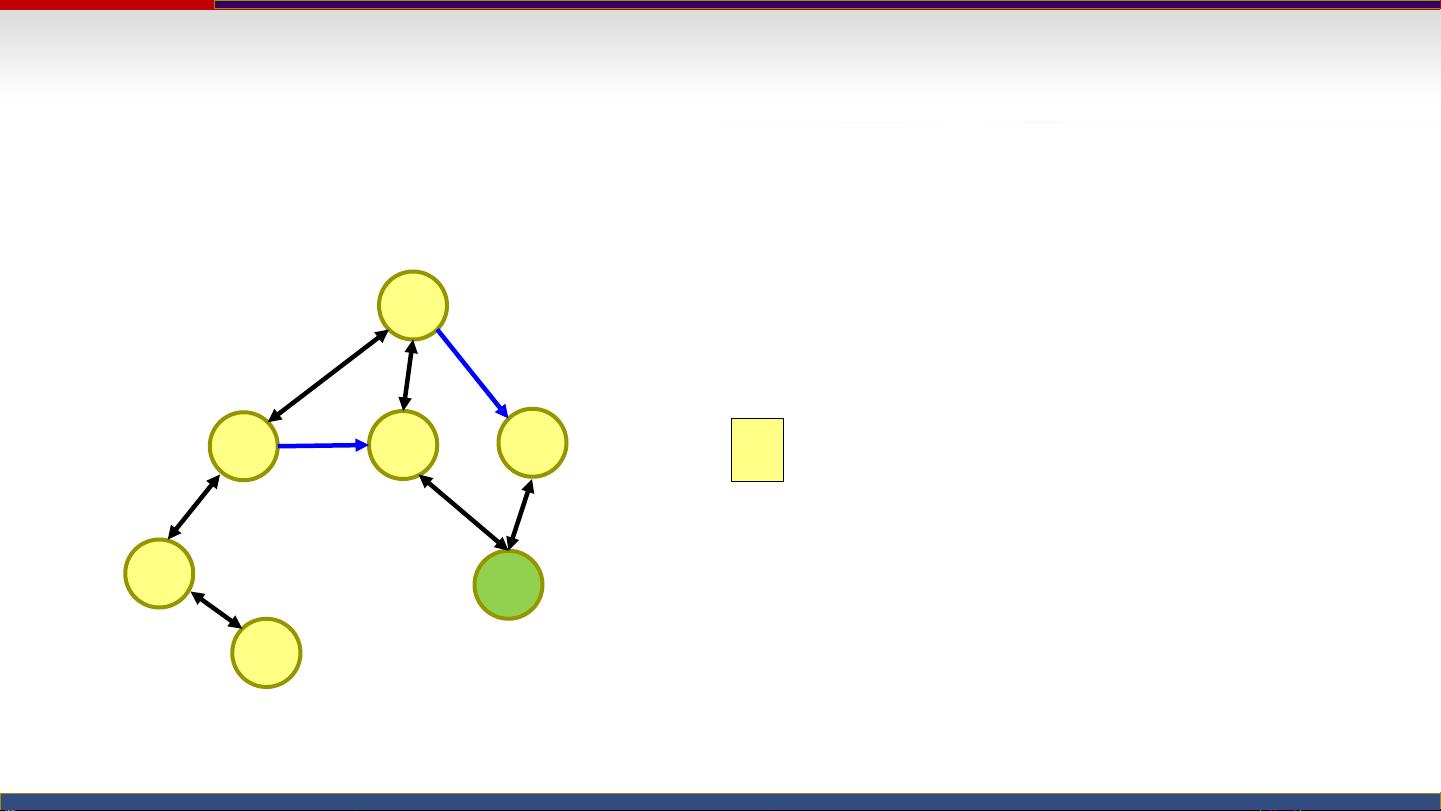
"这篇内容来自北京大学暑期课《ACM/ICPC竞赛训练》，主要讨论了如何使用广度优先搜索（BFS）解决‘抓住那头牛’的问题，这是一个在数轴上寻找最优路径的问题。" 在算法和计算机科学中，广度优先搜索（BFS）是一种用于遍历或搜索树或图的算法。在这个特定的问题中，农夫想要从点N出发捕捉位于点K的牛，农夫有两种移动方式：向左或向右移动一个单位，或者直接跳到当前位置的两倍。目标是找到到达牛的位置所需的最短时间。 首先，我们需要理解BFS的基本思想。BFS从根节点（起点）开始，逐层探索树的分支，先访问离根节点近的节点，再访问远的节点。在图中，这意味着按照距离起点的步数进行搜索，先搜索距离起点最近的节点，然后逐步扩大搜索范围。 在“抓住那头牛”的问题中，我们可以将每个可能的节点位置视为树的一个节点，每一步移动视为边。使用BFS时，我们创建两个数据结构：一个是Open表，存放待处理的节点；另一个是Closed表，存放已处理过的节点。初始时，农夫的位置N加入Open表。每次从Open表中取出最近的一层的节点（即最早放入的节点）放入Closed表，并检查这个节点是否是目标节点。如果目标节点被找到，算法结束，返回最短路径。如果当前节点不是目标节点，那么它的所有未被访问过的相邻节点（即通过两种移动方式可达的节点）被加入Open表，等待后续处理。 对于给定的例子，农夫在点3，牛在点5，最右边是点6。使用BFS，我们可以这样操作： 1. 起点3作为第一层节点放入Open表。 2. 从Open表中取出3，检查是否为5（不是），然后将其放入Closed表。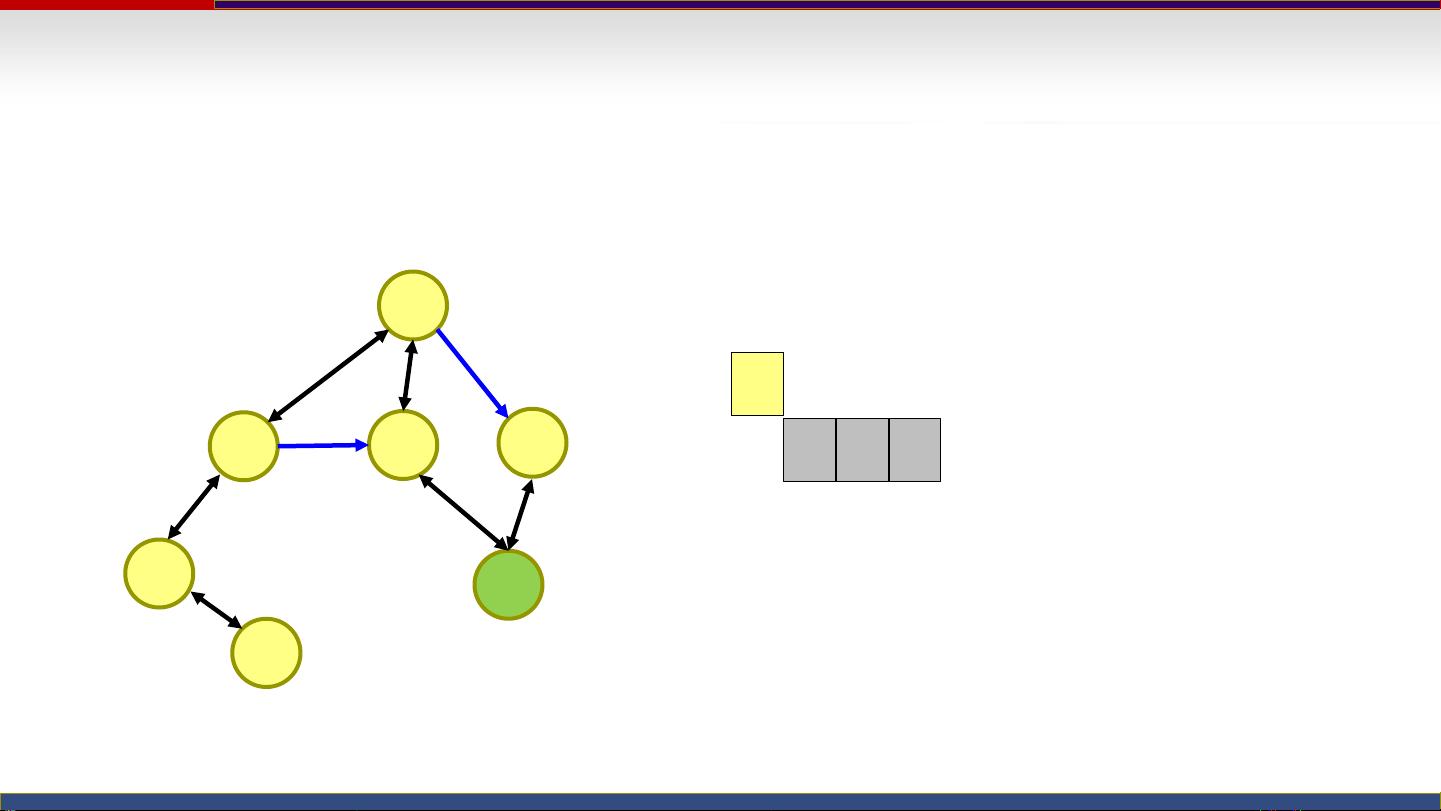 3. 接下来处理3的邻居2、4、6，其中2和4进入第二层的Open表，6因为超出边界不考虑。 4. 从Open表取出2和4，2的邻居1、3、5进入第三层的Open表，4的邻居1、5进入第三层的Open表。 5. 继续这个过程，直到找到牛的位置5，此时我们得到了最短路径，例如3->4->5或3->6->5。 与深度优先搜索（DFS）相比，BFS通常更适用于寻找最短路径，因为它总是先探索最近的节点。DFS可能会陷入局部最优解，而BFS则保证了全局最优性，前提是不存在负权边或成本。 在实现BFS时，可以使用队列来管理Open表，这样可以保证按顺序取出节点。同时，为了避免重复访问节点，需要记录每个节点的状态，通常使用集合或数组作为Closed表。在内存允许的情况下，存储路径上的所有节点以备后用，也可以通过优化仅保留关键节点，例如只保留当前层和下一层的节点，以减少空间消耗。 广度优先搜索是一种强大的工具，尤其在寻找最短路径或解决图论问题时。在‘抓住那头牛’的问题中，BFS提供了一种系统化的方法来找出农夫抓住牛所需的最少时间。