动态规划理论解析：最优子结构、无后效性与重复子问题

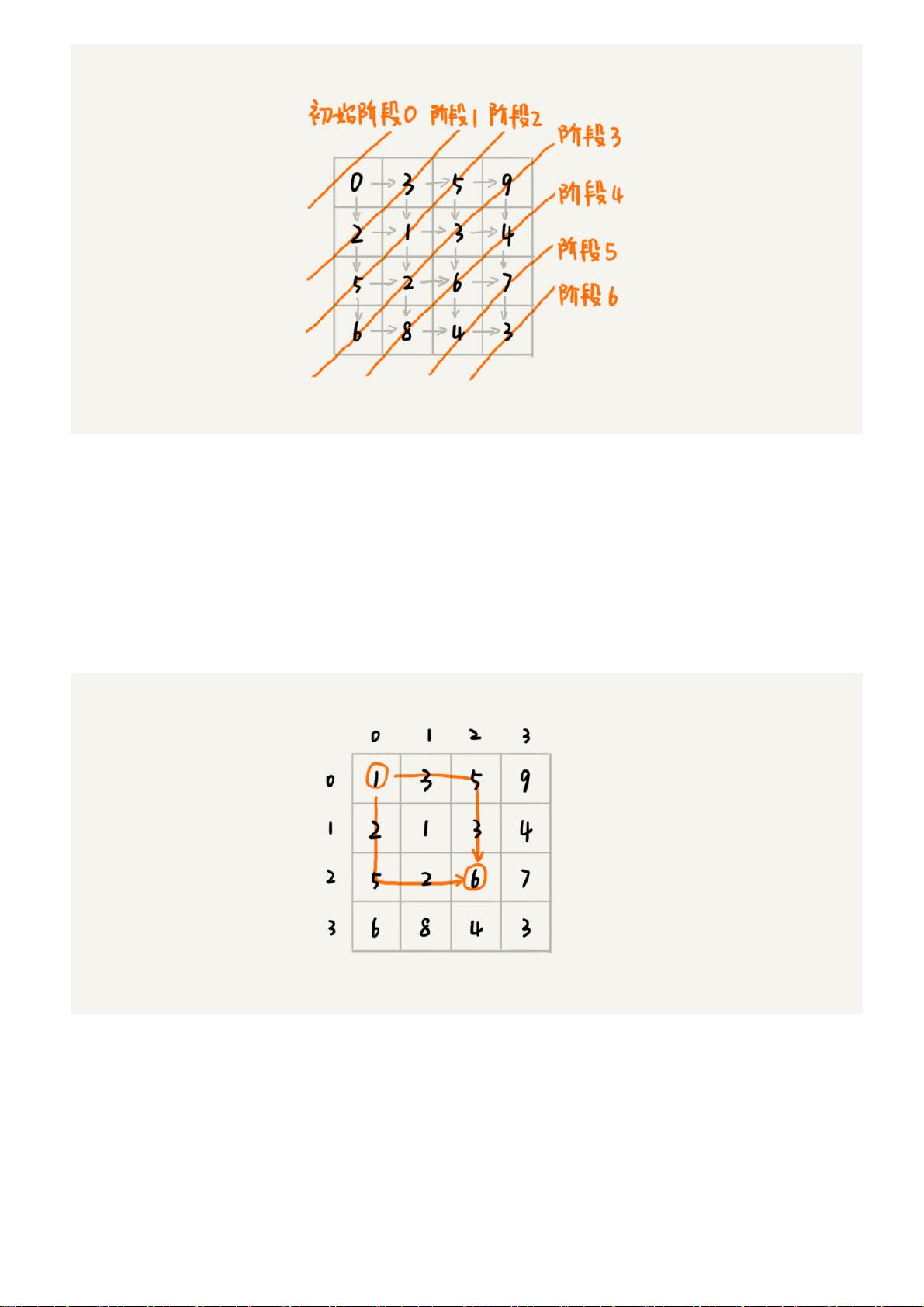
"这篇文章主要介绍了动态规划的基本理论，包括最优子结构、无后效性和重复子问题，并通过'一个模型三个特征'的理论框架进行解析。动态规划是一种用于解决最优决策问题的算法思想，适用于多阶段决策过程，寻找最优解。" 在动态规划中，我们首先要明确的是"一个模型"——多阶段决策最优解模型。这意味着我们要解决的问题通常涉及到一系列的决策步骤，每一步都有可能影响最终结果的最优性。通过一系列决策，我们逐步逼近目标状态，寻找达到期望最优值的决策序列。 接下来，我们深入探讨"三个特征"： 1. **最优子结构**：这是动态规划的核心特性之一。最优子结构意味着问题的全局最优解可以由其子问题的最优解构建。例如，在斐波那契数列问题中，求第n项的最小值可以通过计算第n-1项和第n-2项的最小值来得出。这种特性使得我们可以通过自底向上的方式递归求解问题，避免了重复计算。 2. **无后效性**：这一特征表示在推导当前阶段的状态时，我们只需要考虑之前阶段的状态，而不需要考虑具体如何到达当前状态。也就是说，一旦某个阶段的状态确定，后续的决策不会改变该状态。例如，在背包问题中，一旦物品被选择或舍弃，不会因为后来的选择而改变这一决定。 3. **重复子问题**：动态规划问题往往会出现许多相同或相似的子问题，比如在最长公共子序列问题中，同样的子序列会多次出现。为了提高效率，我们需要存储并重用这些子问题的解，这就是动态规划中的记忆化搜索策略，通过状态转移表或状态转移方程记录和复用已解决的子问题，避免冗余计算。 状态转移表法和状态转移方程法是动态规划常用的两种方法。状态转移表通常是二维数组，用于存储所有可能状态的解，每一行代表一个决策阶段，每一列代表一个状态，通过遍历填表找到最优解。状态转移方程则是描述从一个状态转移到另一个状态的关系式，例如斐波那契数列的问题中，F(n) = F(n-1) + F(n-2)。 了解并掌握动态规划的这些基本理论，可以帮助我们识别适合用动态规划解决的问题，并提供了解决这些问题的思路。动态规划与贪心、分治、回溯等算法思想相比，更注重全局优化，而不仅仅是局部最优。例如，贪心算法往往在每一步选择局部最优解，但不保证整体最优；分治则是将问题分解为独立的部分，然后逐个解决，而动态规划则是在解决子问题的过程中考虑了全局最优。 动态规划是一种强大的工具，尤其在面对具有最优子结构、无后效性和重复子问题的复杂问题时，它的优势尤为明显。通过学习和实践，我们可以更好地运用动态规划来解决实际的计算问题，提高算法的效率和解决方案的质量。