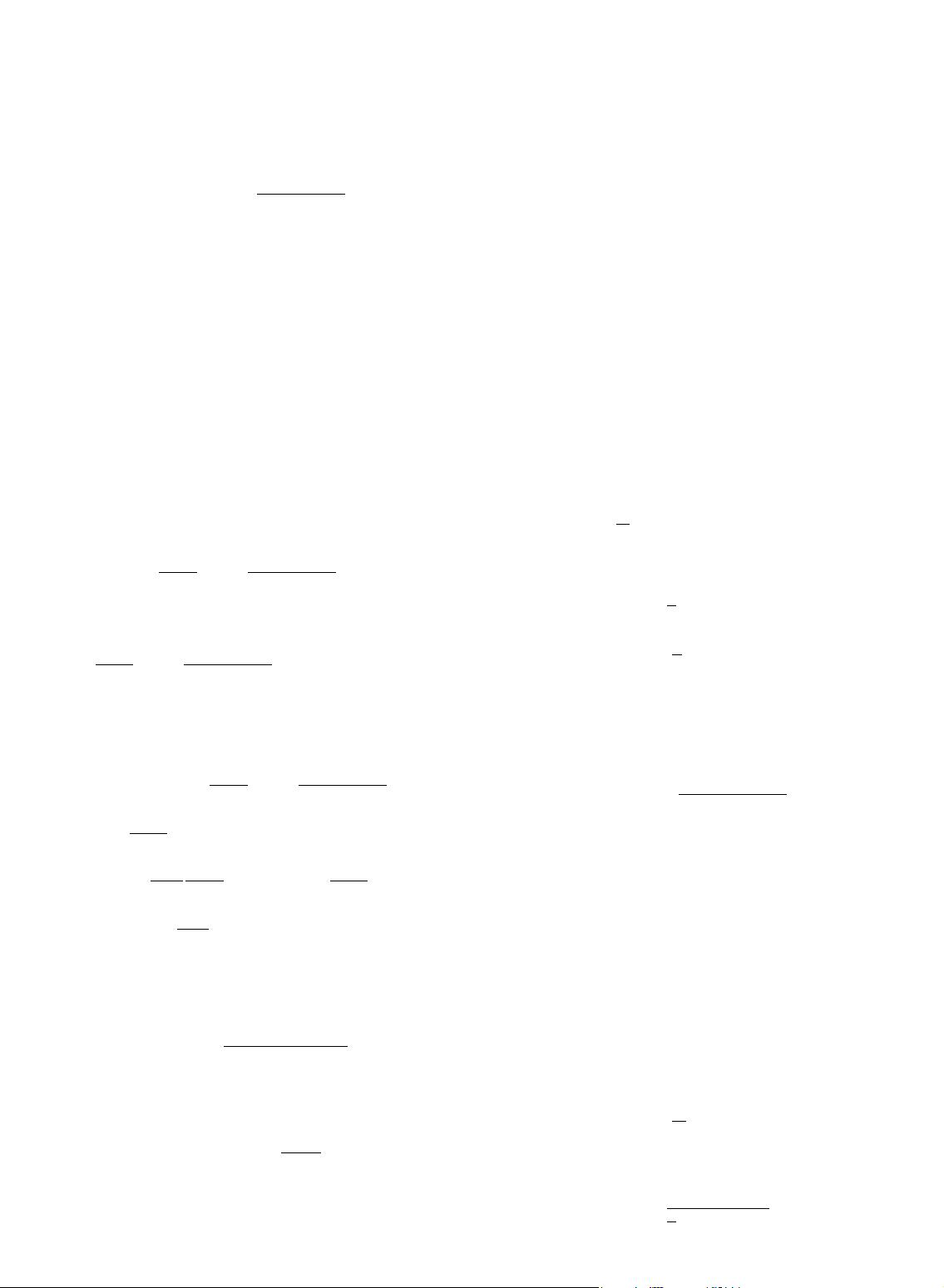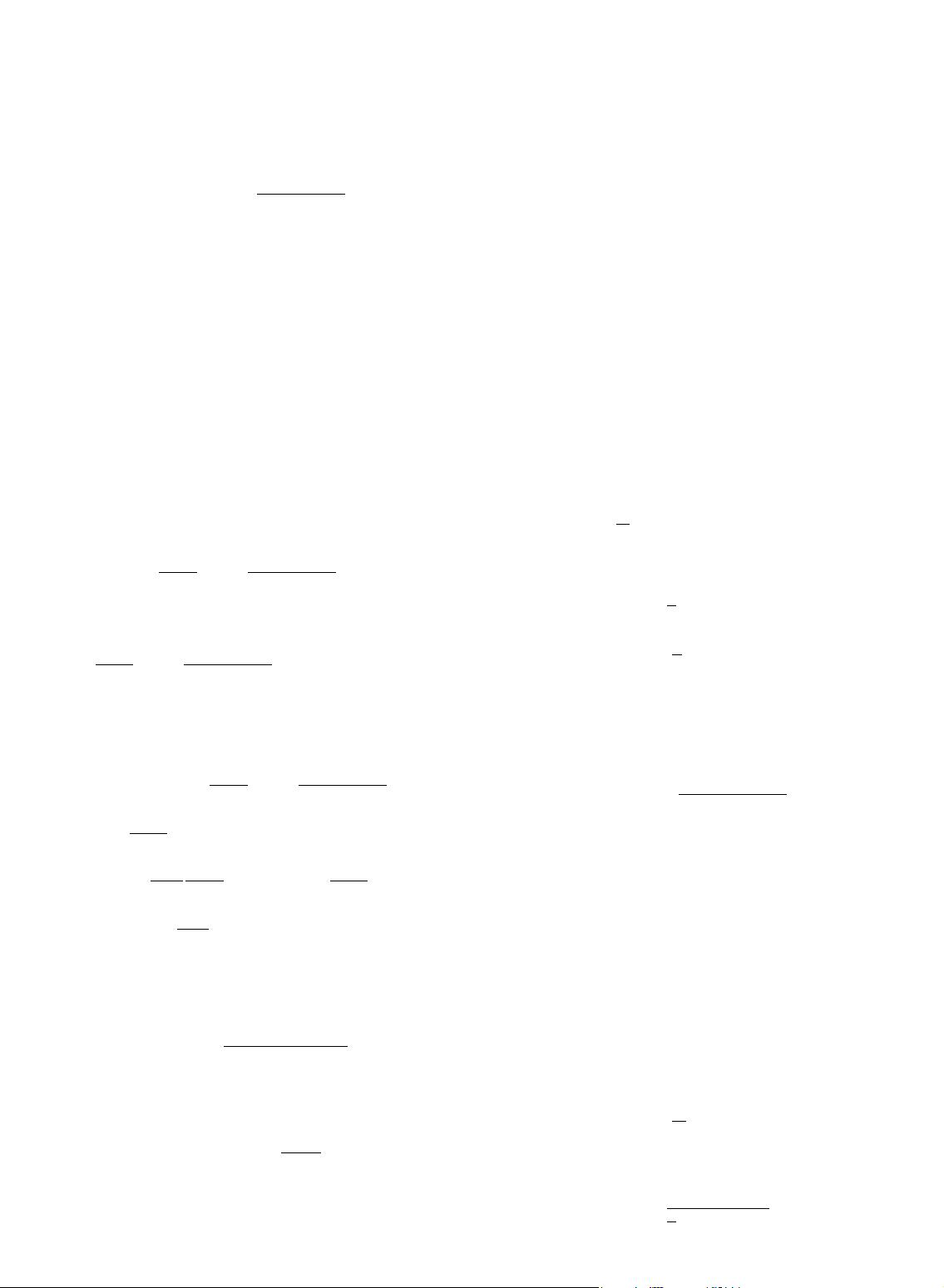
from Shepp and Vardi shows that the RL algorithm can be
considered a maximum likelihood solution using the
Poisson distribution to model the likelihood probability
P ðB; kjIÞ:
P ðB; kjIÞ¼
Y
x2I
gðxÞ
BðxÞ
e
gðxÞ
BðxÞ!
; ð4Þ
gðxÞ¼
X
y2k
IðyÞkðx yÞ; ð5Þ
where B is the observed motion blurred image, k is the
motion PSF, i.e.,
P
y2k
kðyÞ¼1, I is the clear image we want
to estimate, and gðxÞ is a convolution process for a pixel
located at x. Equation (4) assumes that the likelihood
probability is conditionally independent for each x. Since
P
y2k
kðyÞ¼1 and
P
x2B
BðxÞ¼
P
x2I
IðxÞ, the overall in-
tensity is preserved.
In [26], Shepp and Vardi show that (4) is a concave
function by showing the matrix of second derivatives of (4)
is negative semidefinite. In order to optimize (4), it follows
from Theorem 2.19(e) of [30] that the sufficient conditions
for I to be a maximizer of (4) are the Kuhn-Tucker
conditions, where all x satisfy
IðxÞ
@
@IðxÞ
ln
Y
x2I
gðxÞ
BðxÞ
e
gðxÞ
BðxÞ!
!
¼ 0 ð6Þ
and
@
@IðxÞ
ln
Y
x2I
gðxÞ
BðxÞ
e
gðxÞ
BðxÞ!
!
0; if IðxÞ¼0: ð7Þ
To obtain the iterative update rule for the RL algorithm,
we use the first condition in (6),
2
for all x 2 I:
IðxÞ
@
@IðxÞ
ln
Y
x2I
gðxÞ
BðxÞ
e
gðxÞ
BðxÞ!
!
¼ 0;
IðxÞ
X
x2I
@
@IðxÞ
ðBðxÞlnðgðxÞÞ gðxÞlnðBðxÞ!ÞÞ ¼ 0;
IðxÞ
X
x2I
BðxÞ
gðxÞ
@
@IðxÞ
gðxÞIðxÞ
X
x2I
@
@IðxÞ
gðxÞ¼0;
IðxÞ
X
y2k
BðyÞ
gðyÞ
kðy xÞIðxÞ
X
y2k
kðy xÞ¼0:
Since
P
y2k
kðyÞ¼1, we have
P
y2k
kðy xÞ¼1. After
adding the iteration index t, we get
I
tþ1
ðxÞ¼I
t
ðxÞ
X
y2k
BðyÞ
P
z2k
I
t
ðzÞkðy zÞ
kðy xÞ: ð8Þ
Utilizing the convolution operation for the whole image, we
obtain the RL algorihm
I
tþ1
¼ I
t
~
k
B
k I
t
; ð9Þ
where
~
k is the transpose of k that flips the shape of k
upside-down and left-to-right, is th e convolution
operation, and is a pixel-wise multiplication operation.
To understand (9), we can consider that B
0t
¼ k I
t
is the
prediction of a blurred image according to the current
estimation of clear image I
t
and the given point spread
function k. Thus, B=B
0t
is the residual errors (by pixelwise
division) between the real blurred image B and the
predicted blurred image B
0t
. The correlation operation
ð
~
kÞ integrates the residual errors distributed according to
~
k. The update rule in (9) essentially computes a clear
image I
1
that would generate the blurred image B, given a
known point spread function k. Typically, the algorithm
starts with an initial guess of I
0
¼ B.
4.2 Projective Motion Rich ardson-Lucy Algorithm
With the basic Richardson-Lucy algorithm, we can derive
our projective motion Richardson-Lucy algorithm. From the
projective motion blur mod el defined in (3), we can
integrate the motion path at each pixel location y and
define a spatially varying motion PSF k
y
:
BðyÞ¼
1
N
X
N
i¼1
IðH
i
xÞ¼
X
x2k
y
IðxÞk
y
ðxÞð10Þ
and
k
y
ðxÞ¼
1
N
;ifx¼ H
1
i
y
0; otherwise;
ð11Þ
where
P
x2k
y
k
y
ðxÞ¼
P
N
i¼1
1
N
¼ 1. Because x ¼ H
1
i
y does
not correspond to a discrete integer pixel coo rdinate,
bicubic interpolation is used to estimate the pixel values
for the points x.
Substituting and replacing (5) with (10) for the RL
algorithm, we get
I
tþ1
ðxÞ¼I
t
ðxÞ
X
y2k
x
BðyÞ
P
z2k
y
I
t
ðzÞk
y
ðzÞ
~
k
x
ðyÞ; ð12Þ
which is the general form for spatially varying motion
deblurring using the RL algorithm. The motion path in
~
k
x
is
the reverse direction of motion path in k
x
.
Since the motion path in k
x
according to (10) can be
described by a sequence of homographies, H
1
...H
N
,we
can also group the motion path of
~
k
x
. Grouping the motion
path of
~
k
x
forms a new sequence of homographies, which is
the original homography sequence but with each matrix
inverted and applied in reverse order, i.e., H
1
N
...H
1
1
. For
each point along the motion path in H
1
...H
N
, H
1
N
...H
1
1
reverse the transformation and integrate the errors along
the motion path. Thus, we obtain the iterative update rule
for the projective motion blur model
I
tþ1
¼ I
t
1
N
X
N
i¼1
E
t
ðH
1
i
xÞ; ð13Þ
where
E
t
ðxÞ¼
BðxÞ
1
N
P
N
i¼1
I
t
ðH
i
xÞ
1606 IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 33, NO. 8, AUGUST 2011
2. The second condition in (7) is used to relate the RL algorithm with the
EM algorithm [9] for the convergence proof. For further details, we refer
readers to [26].