哈工大《概率论》期末复习重点：选择题与填空题解析

"哈尔滨工业大学《概率论》期末复习资料包含了选择题和填空题，涵盖了概率论中的独立事件、方差、正态分布、检验统计量等核心概念。" 一、选择题解析： 1、独立事件的定义是，事件A与事件B发生与否互不影响，数学上表示为P(A|B) = P(A) 和 P(B|A) = P(B)。题目中给出的选项，只有(B)符合这个定义，即P(A|B) = P(A) * P(B)。 2、由D(X+Y) = D(X-Y)可推断出协方差Cov(X,Y) = 0，但不能直接得出D(Y) = 0或X与Y独立。因此，(A)和(B)都不正确。不相关意味着协方差为零，所以(C)正确，而(D)DXDY=0是说X和Y的乘积的期望值为零，这不是必要的条件。答案是(C)。 3、二维随机变量(X,Y)~N(1，1；1,2^2；0)表示X与Y是独立的正态分布，其中X的方差为1，Y的方差为2^2=4。D(-2XY+3) = (-2)^2 * D(XY) + D(3) = 4 * D(X) * D(Y) = 4 * 1 * 4 = 16，但这不是选项之一。可能题目有误，但按照现有信息，答案没有直接对应项。 4、随机变量X服从N(μ, σ^2)的正态分布，σ增大不会改变μ值，因此P(μ-σ<X<μ+σ)的概率，即概率密度函数的峰值，保持不变。答案是(C)。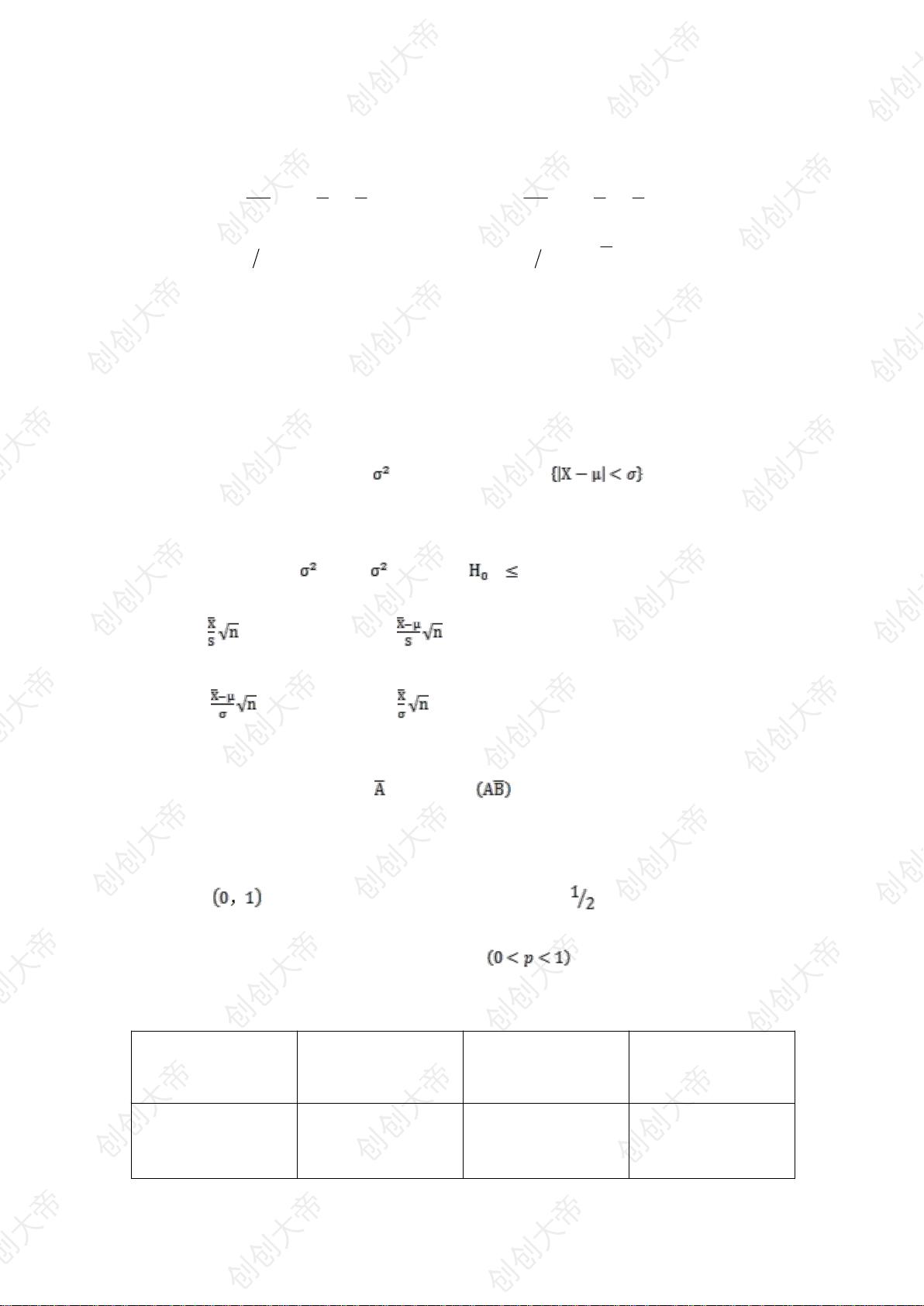 5、对总体X~N(μ, σ^2)，检验μ0时，若总体方差未知，应使用t统计量，因此选择(B) t==。 二、填空题解析： 1、如果事件A与B互斥，即它们不能同时发生，那么P(A∪B) = P(A) + P(B)，题目中P(A∪B) = 0.8，P(B) = 1 - P(A)，所以P(A) = 0.8 - P(B)。 2、两个人取球的问题属于条件概率，第一人取到黄球的概率不影响第二人取到黄球的概率，因此第二人取到黄球的概率是20/50 * 19/49。 3、在[0,1]中随机取两个数，其差的绝对值小于ε的概率可通过几何方法计算，涉及二维均匀分布。 4、这个问题描述了一个负二项分布，X表示在n次成功前失败的次数，P(X=k) = C(k-1, n-1) * p^(k) * (1-p)^(n-k)，其中p是每次成功的概率。 5、边缘分布函数是联合分布函数对某一个变量积分的结果。此处需计算对Y的边缘分布，分别对X=0, 2, 4时对应的概率求和。 6、切比雪夫不等式用于估计离均值的距离大于某个值的概率，对于EX=1，DX=4，可以估算P(|X-1| >= k)的上限。 7、这个统计量可能是样本均值的平方，因为它通常用于检验正态分布的总体均值的平方。 8、当样本容量为9且样本均值为5时，根据正态分布的性质，可以构建一个t分布来估计μ的置信区间。 以上是对题目内容的部分解析，具体答案需要进一步计算或详细阅读资料来确定。这些题目覆盖了概率论的关键概念，包括独立事件、概率分布、统计推断和不等式等。