非牛顿流体在偏心圆环管中的数值模拟

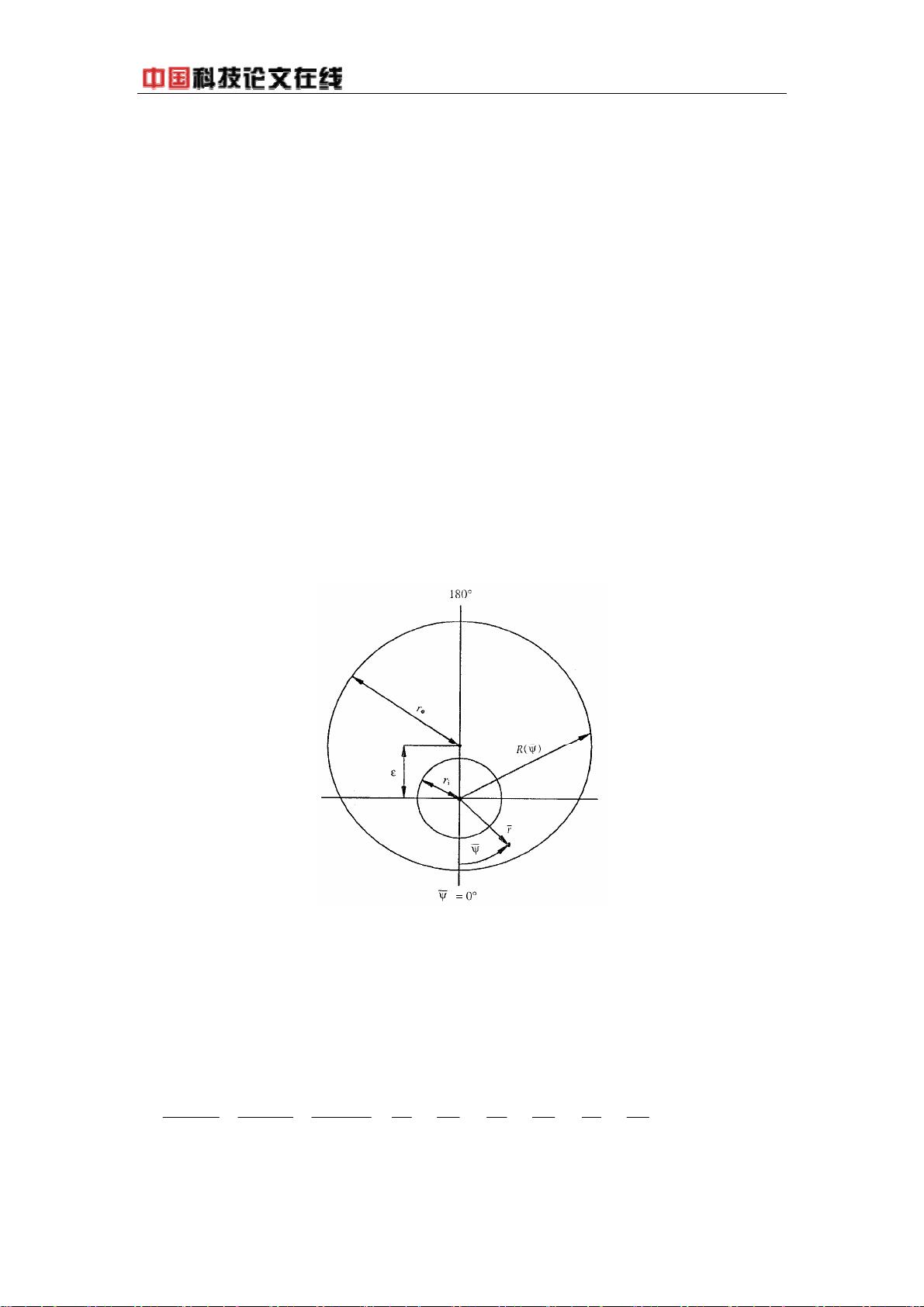
"偏心圆环管中非牛顿流体充分发展层流的数值计算" 在非牛顿流体力学领域，偏心圆环管内的流体流动问题是一个重要的研究课题，尤其对于涉及石油、化工和食品加工等行业的工程应用。非牛顿流体是指那些剪切应力与剪切速率之间并非线性关系的流体，它们的流变性质取决于剪切力的作用。在实际应用中，由于制造误差或机械振动，圆环管往往会出现偏心现象，这会显著影响流体的流动特性。 传统的数值模拟方法通常使用结构化网格和有限差分法，但这种方法在处理偏心圆环管等不规则几何形状时面临挑战，因为需要进行坐标变换，增加了计算的复杂性。相比之下，非结构化网格因其对不规则区域的高适应性而受到青睐。非结构化网格允许在直角坐标系下直接离散控制方程，简化了计算过程。 在本研究中，作者马倩、张敏和许彬采用基元中心有限容积法在非结构化网格上对非牛顿流体在偏心圆环管中的流动进行了数值模拟。这种方法无需进行复杂的坐标变换，能够更方便地处理不规则边界条件。他们考察了不同偏心率和半径比下的速度场分布，以揭示流体流动的规律。这些结果对于理解和优化工业过程中的流体流动和传热现象具有实际意义。 具体来说，研究中使用了三维笛卡尔坐标系下的定常通用输送方程，并针对充分发展层流进行了简化假设，仅考虑沿流动方向（Z方向）的速度分布。控制方程包括质量守恒、动量守恒和扩散效应，其中，φ代表速度分量或温度等物理量，ρ表示流体密度，S为源项，Γ为扩散系数。通过离散这些方程，研究人员能够在非结构化网格上求解流场，从而得到速度分布和温度分布等关键信息。 与结构化网格计算结果的比较验证了该非结构化网格方法的准确性和实用性。这种数值计算方法的应用不仅可以帮助工程师理解偏心圆环管中非牛顿流体的流动行为，还能为相关领域的设计和优化提供理论依据，从而提高设备效率和过程稳定性。 这项研究深入探讨了非牛顿流体在偏心圆环管中的流动特性，通过数值计算揭示了流动规律，为实际工程问题提供了理论支持。采用非结构化网格的方法不仅简化了计算流程，而且提高了计算精度，为未来类似复杂几何形状的流体流动问题研究提供了新的思路。