并行算法在微波电路计算中的应用与实现

"本文介绍了在微波电路设计中应用并行算法的一种方法，旨在解决随着频率升高，计算需求急剧增加的问题。传统的时域有限差分法（FDTD）在处理高频电磁问题时面临挑战，因为计算网格会变得非常庞大，对计算机性能要求极高。为了改善这一状况，文章引入了Diakoptics的概念，这是一种源自网络理论的分解方法，通过将微波电路分割为多个独立部分，使用不同的网格进行全波时域分析，以提高计算效率和收敛性。并行Diakoptics允许在网络的不同子部分之间进行并行计算，减少了对单一计算资源的依赖，提高了整体计算速度。 一、时域有限差分法（FDTD）的基本原理 时域有限差分法是基于时域麦克斯韦方程的数值解法，由K.S.Yee在1966年提出。该方法将连续的场分量转化为离散的差分形式，通过迭代计算来模拟电磁场的演化。然而，随着频率的增加，需要更精细的网格以准确模拟，导致计算量呈指数级增长，单靠提升计算机性能难以满足需求。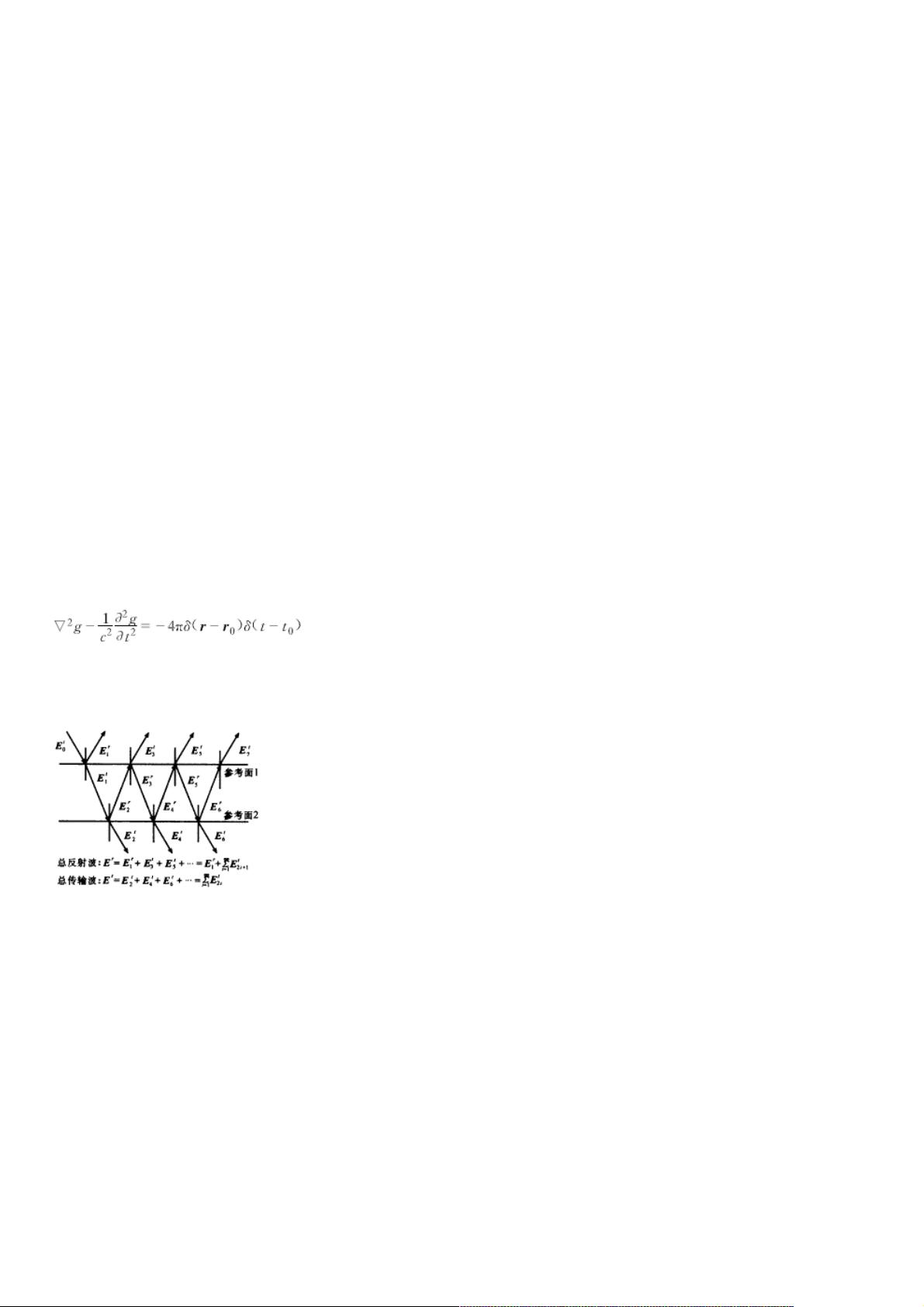 二、Diakoptics在微波电路分析中的应用 Diakoptics的核心思想是将复杂的电路分解为若干简单的子网络，分别计算每个子网络的冲击响应，然后利用适当的连接条件组合这些子网络的响应，得到整个网络的响应。在微波电路的全波分析中，这种方法允许对每个子网络使用适合其几何特性的网格，确保算法的稳定性和收敛性。 1. 串行连接与并行连接 Diakoptics提供了串行连接和并行连接两种方式。串行连接按照特定顺序逐个处理子网络，虽然简单，但若一个子网络的响应改变，可能影响后续子网络。并行连接则可以避免这个问题，允许在多个子网络之间同时进行独立计算，提高了计算效率。 2. 并行时域Diakoptics 在并行连接中，子网络可以视为M+N端口的系统，M个端口连接前一个子网络，N个端口连接后一个子网络。每个子网络的离散格林函数g(i,j,n')是关键参数，它描述了子网络对输入信号的响应。 三、并行计算的优势 并行Diakoptics的优势在于： - 提高计算效率：通过并行化处理，减少了计算时间，尤其对于大规模微波电路问题，效果显著。 - 资源优化：不同子网络可以在不同的计算节点上并行运行，充分利用多核处理器或分布式计算资源。 - 收敛性保证：每个子网络使用均匀网格，有助于保持算法的稳定性，提高收敛速度。 四、实际应用与未来发展 这种并行算法计算方法已经在微波电路设计和工业控制中得到了应用，例如波导滤波器的分析。未来，随着硬件技术的进一步发展，如GPU加速和云计算平台的普及，这种并行计算策略有望在更多复杂的电磁问题中发挥更大的作用，为微波电路设计提供更高效、精确的解决方案。