贝叶斯决策理论在细胞识别中的应用

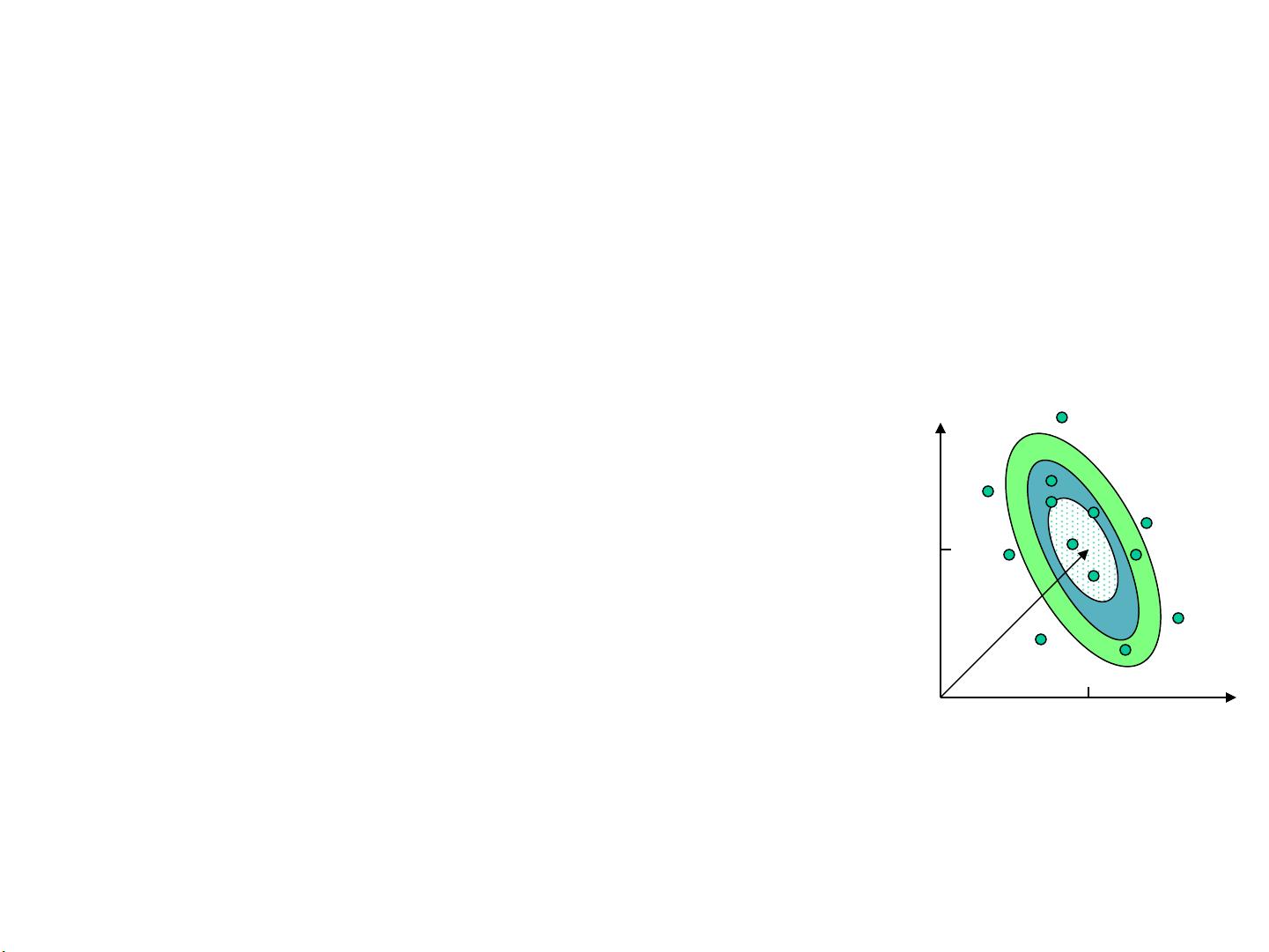
"本资源主要介绍了贝叶斯分析和学习理论在决策理论中的应用，特别是贝叶斯分类器的概念和实现。内容涵盖了正态分布决策理论、错误率分析、最小风险Bayes分类器以及聂曼-皮尔逊判别准则和最大最小判别准则。此外，还讨论了决策树和序贯分类等方法，并通过细胞识别问题举例说明如何利用贝叶斯公式进行概率修正和最优分类。" 贝叶斯分析是一种在不确定性和不完全信息下的统计决策方法，它基于贝叶斯定理来更新我们对未知事件发生概率的理解。在贝叶斯决策理论中，我们首先根据现有数据设定一个先验概率，然后随着新数据的获取，使用贝叶斯公式来不断调整这个概率，形成后验概率。这一过程使得我们的决策更加基于最新的观测结果。 贝叶斯分类器是贝叶斯决策理论的一个具体应用，它寻找将样本分配到不同类别时的最优策略。在两类问题中，比如细胞识别，我们有两类细胞（正常和异常），并且可以通过统计先验概率P(ω1)和P(ω2)来初步判断。然而，仅依赖先验概率进行分类往往是不够准确的。通过引入类条件概率密度P(x/ω1)和P(x/ω2)，我们可以计算出每个样本属于某一类别的后验概率。当样本的特征x被观察到后，这些后验概率可以用来更精确地识别细胞类型。 贝叶斯分类器的决策规则通常是基于后验概率的最大化。例如，将样本分配到后验概率最高的类别。有多种形式的贝叶斯判别函数，如直接比较后验概率或使用对数似然比。在实际应用中，还需要考虑错误率分析，以便理解分类器可能出现的误判情况。最小风险Bayes分类器旨在最小化总的错误成本，而不仅仅是错误率。 此外，聂曼-皮尔逊判别准则和最大最小判别准则是两种常见的分类准则，它们分别基于似然比和风险函数来进行决策。决策树是一种直观的分类工具，通过构建一系列的判断节点来引导分类过程。序贯分类则是在数据收集过程中逐步进行的分类，允许在获取更多信息后调整决策。 贝叶斯分析和学习理论提供了一种强大的工具集，用于处理不确定性和复杂数据的决策问题。通过理解并应用这些理论，我们可以构建更智能、更适应环境变化的分类模型，尤其在生物医学、信息检索、金融风险评估等多个领域有着广泛的应用。