线性系统辨识与自适应控制：第3讲-最小二乘法

"系统辨识及自适应控制课件第三讲涵盖了系统辨识的基础知识，主要讲解了系统和模型的概念，辨识的定义、步骤，以及线性系统辨识问题的表达形式和最小二乘格式。课程聚焦于线性系统的模型类和线性模型的选择，同时介绍了基于ARX模型的最小二乘法建模方法。" 系统辨识是控制理论中的一个重要分支，它涉及对物理系统的数学模型进行估计和构建，以便更好地理解和预测系统的行为。本讲主要围绕以下几个核心知识点展开： 1. **系统和模型**：在工程应用中，当输入信号在工作点附近变化不大时，许多系统可以近似视为线性系统。线性系统是指输出与输入之间存在线性关系的系统。线性模型类包括一组待确定的参数，可以用来拟合实际系统的行为。 2. **辨识的定义和三要素**：辨识是通过实验数据来确定系统模型的过程，主要包括三个要素：实验设计（输入信号的选择）、数据处理和模型结构选择。 3. **线性系统辨识问题的表达形式**：线性系统辨识通常采用最小二乘格式，寻找使得预测误差平方和最小的参数值。这种表达形式可以清晰地表示出模型与实际数据之间的拟合关系。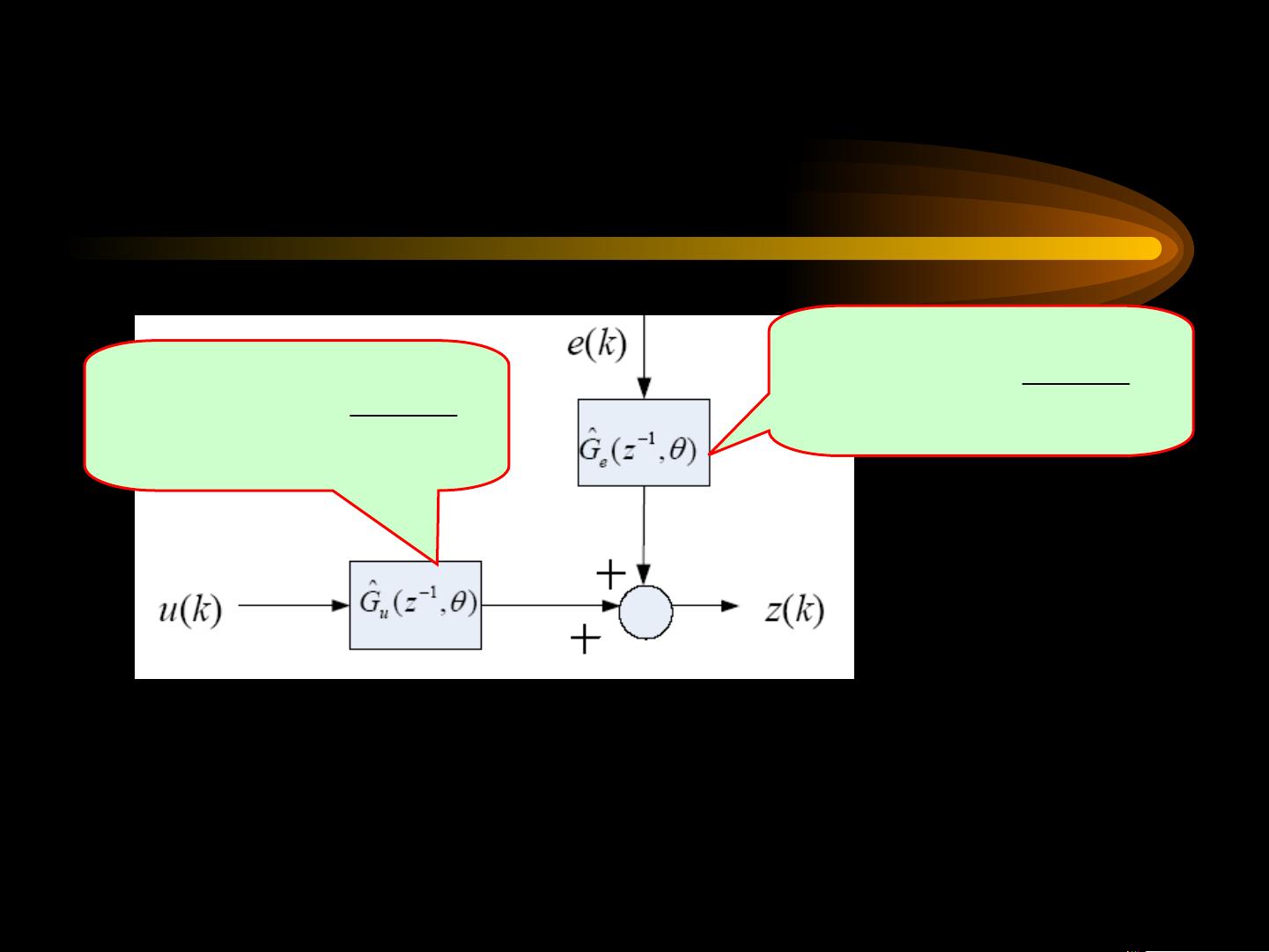 4. **最小二乘格式**：在ARX（AutoRegressive eXogenous）模型中，最小二乘法是一种常用的参数估计方法。ARX模型描述了系统输出如何依赖于过去的输入和输出值。最小二乘法通过最小化预测误差的平方和来估计模型参数，简化了模型求解过程。 5. **ARX模型**：ARX模型的结构为输出y_k与过去n个输入u_k和输出z_k的函数关系，即y_k = a_1*z_{k-1} + ... + a_n*z_{k-n} + b_1*u_{k-1} + ... + b_m*u_{k-m}。通过最小二乘法，可以找到最佳的系数a_i和b_j，使得模型输出与实际输出的误差最小。 通过这些基础知识的学习，可以为后续的自适应控制打下坚实的基础。自适应控制是一种动态调整控制器参数的方法，使其能够自动适应系统参数的变化或未知特性，从而实现对系统的有效控制。在实际工程应用中，系统辨识与自适应控制相结合，能够提高控制系统性能和鲁棒性。