数理逻辑在高级人工智能中的应用

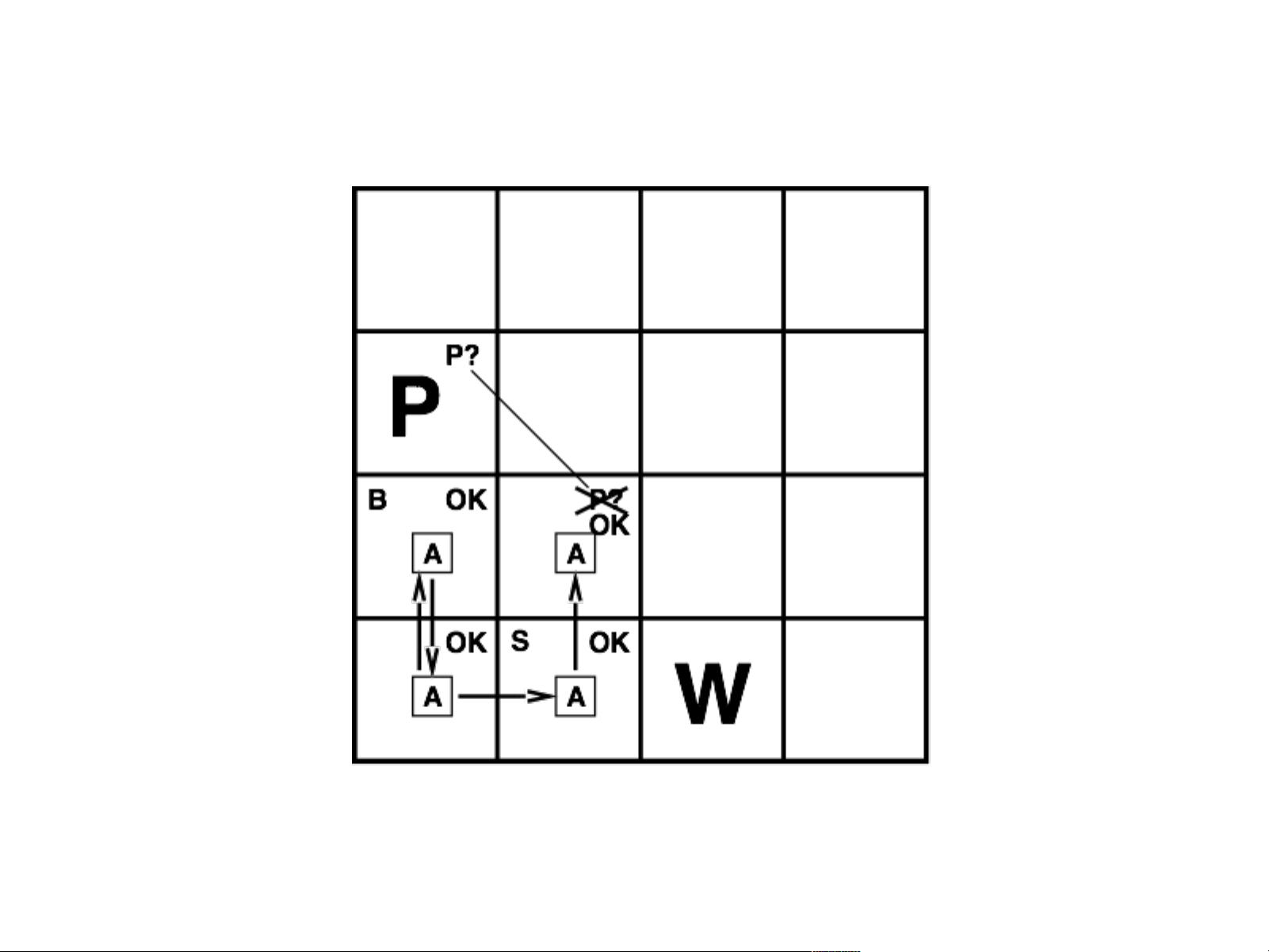
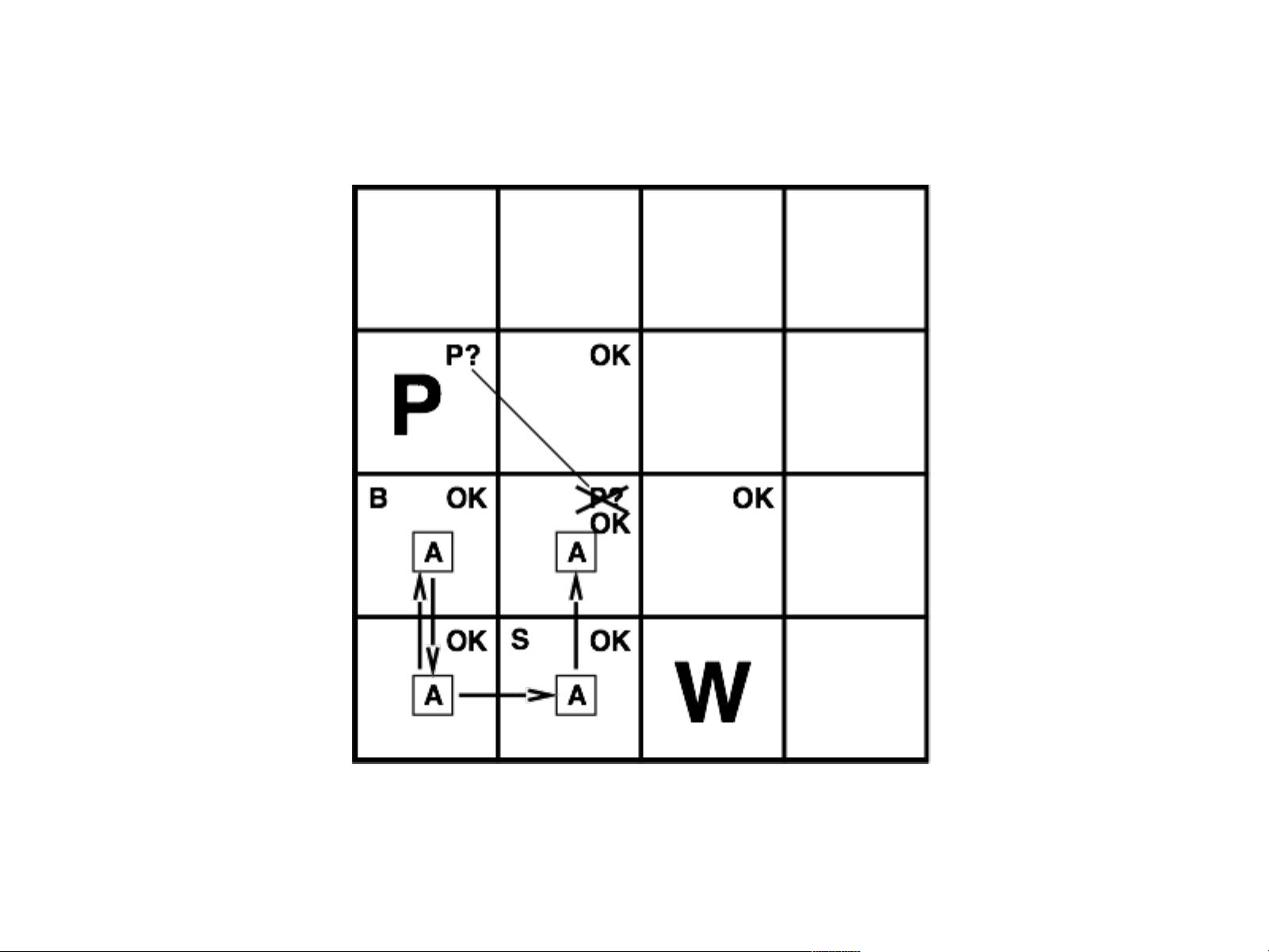
"高级人工智能，数理逻辑" 在高级人工智能领域，数理逻辑扮演着至关重要的角色，它为理解和构建智能系统提供了基础理论框架。数理逻辑主要研究形式化的句子之间的关系，包括语义和语法两个角度。台湾大学的于天立教授在“人工智慧”课程中深入探讨了这一主题，这门课程可以作为深入学习的资源。 1. 语义与逻辑推导（Entailment） 语义研究的是句子之间的蕴含关系，即一个或一组句子是否逻辑地蕴涵另一个句子。例如，在数学中，如果表达式 "X+Y=4" 成立，那么 "X=0, Y=4" 是这个表达式的模型，意味着它满足了原始表达式的条件。这种关系称为Entailment。 2. 语法与形式推演（Deduction） 语法方面关注的是如何通过形式规则进行演绎推理。形式推演是一种逻辑证明方法，它遵循特定的逻辑规则，从前提中推导出结论。例如，命题逻辑中的推理规则如假言推理、三段论等，用于构造形式证明。 3. Wumpus World与PEAS描述 在AI的教学中，Wumpus World是一个经典的环境模型，用来教授问题解决和规划。PEAS描述（Purpose, Environment, Actuators, Sensors）是一种系统分析工具，用于理解一个智能体在环境中如何行动。在Wumpus World中，逻辑被用来分析可能的洞穴布局，判断是否有危险（如Wumpus或陷阱），并规划安全的探索路径。 4. 命题逻辑（Propositional Logic） 命题逻辑是逻辑学的基础，关注的是简单命题（Atomic propositions）的真假。这些命题不考虑时间变化，但当命题的真值随时间变化时，我们将其称为“fluent”，比如“今天是周一”。命题逻辑包括语法和语义两部分： - 语法：定义了命题的构成规则，如联接词（与、或、非等）和括号，以及如何组合原子命题形成复合命题。 - 语义：解释了命题的真值，例如，真值表用于确定复合命题在所有可能情况下的真假。 学习数理逻辑对于理解人工智能中的推理、知识表示、自动定理证明以及机器学习的理论基础至关重要。通过阅读教材《人工智能：一种现代的方法》（AIMA）的中英文版本，观看陆钟万教授的授课视频，以及参与于天立教授的在线课程，可以深入理解这些概念，并提升在高级人工智能领域的专业素养。