武汉大学概率论与数理统计课程介绍

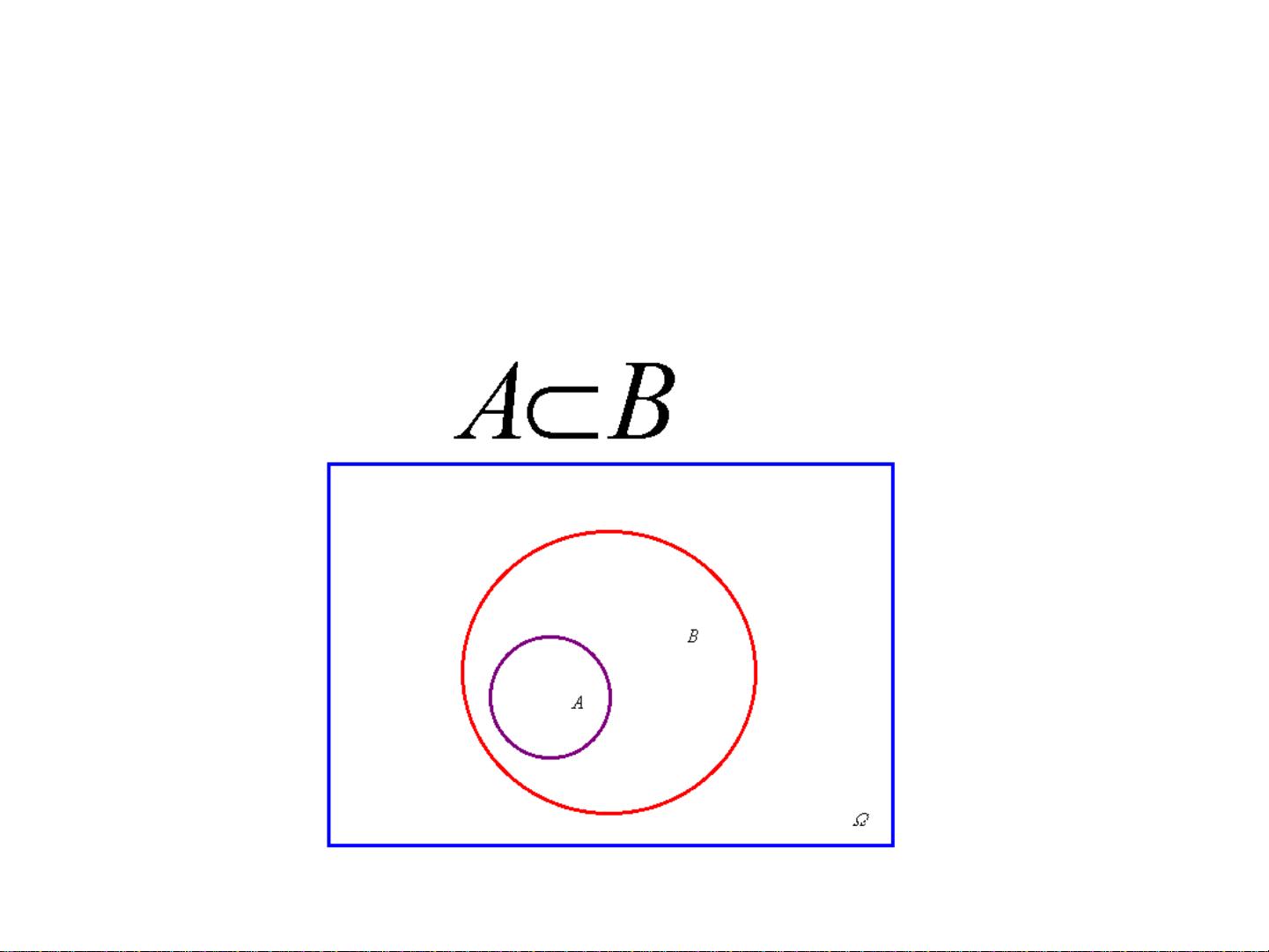
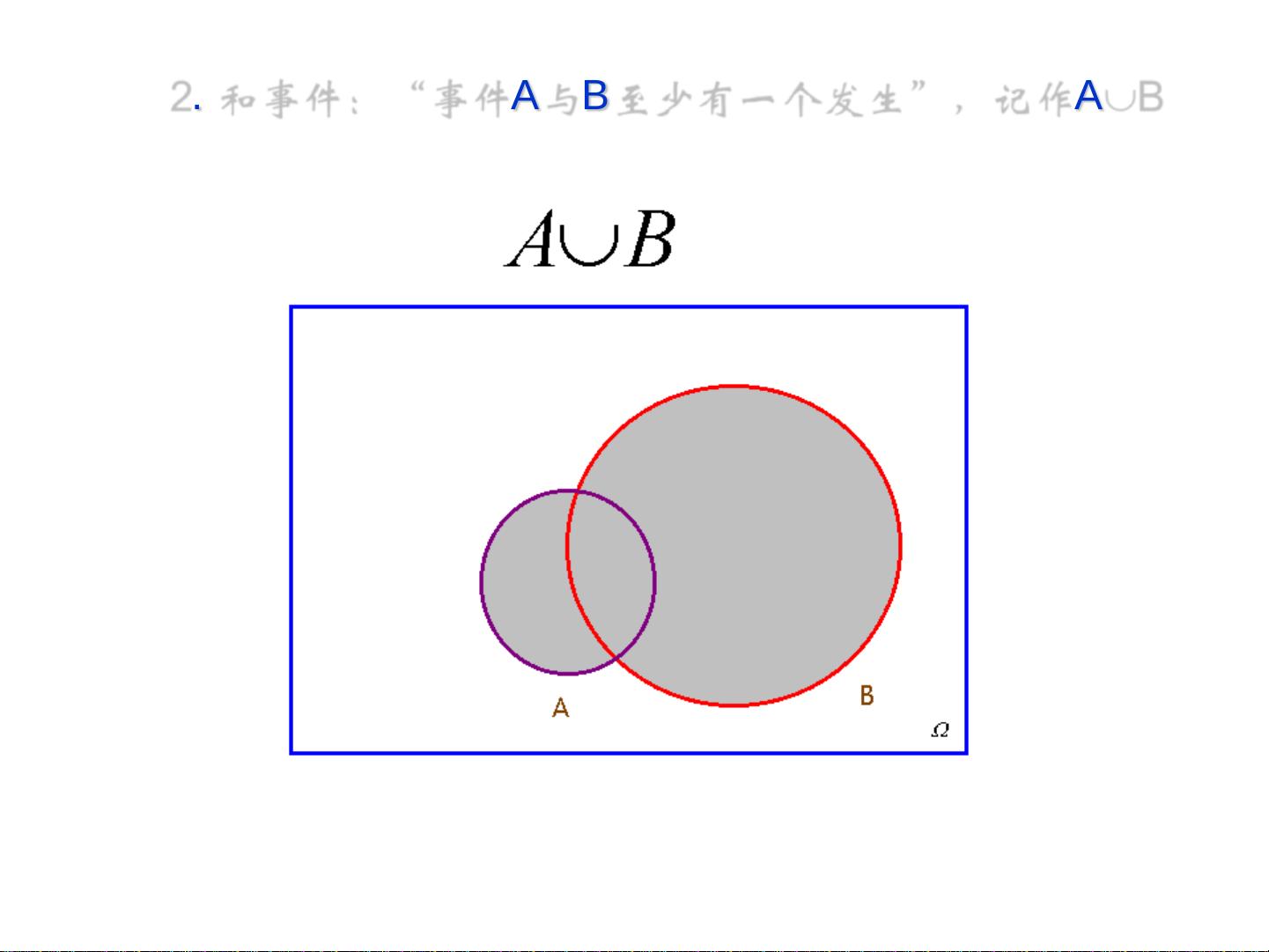
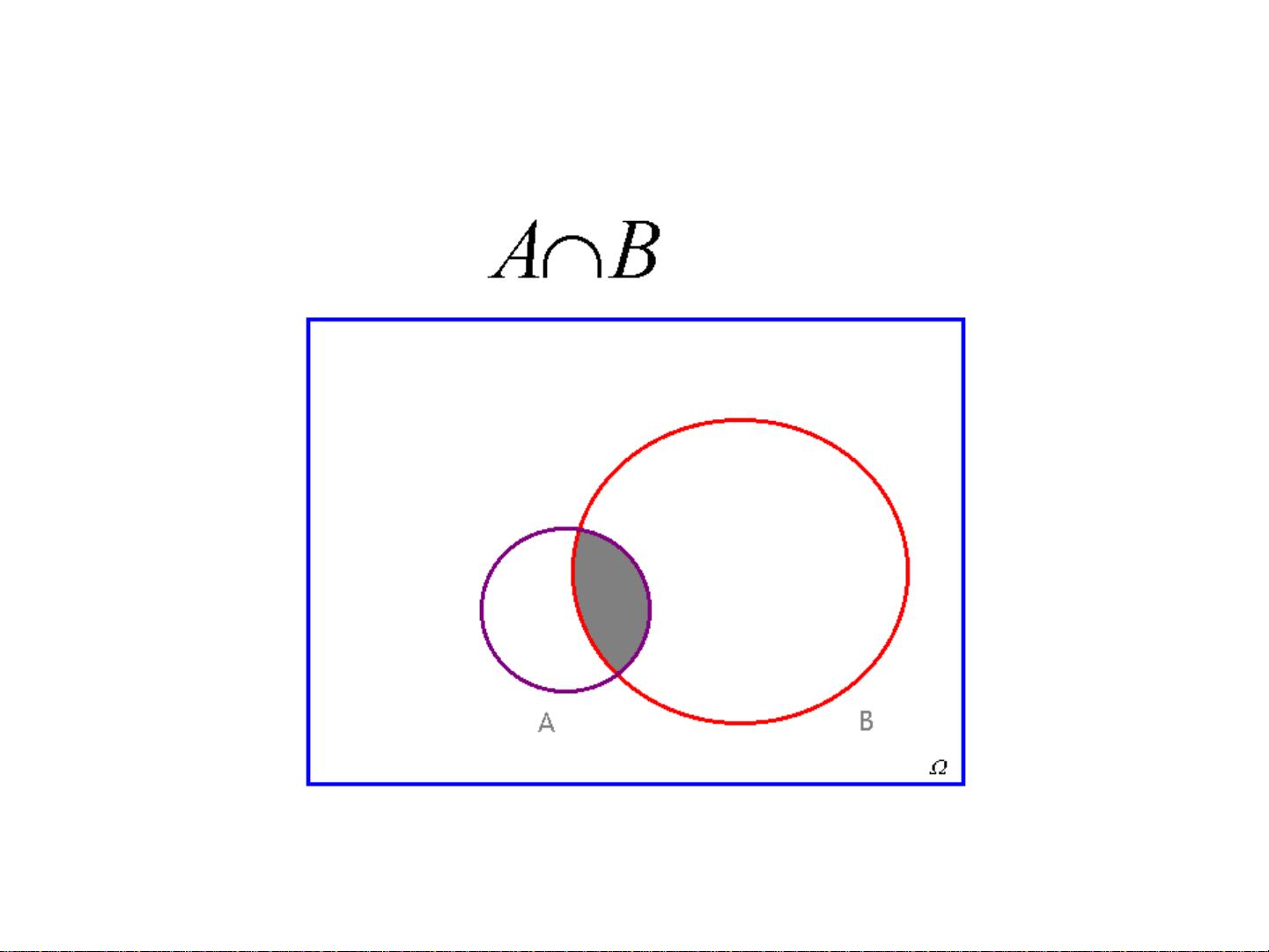
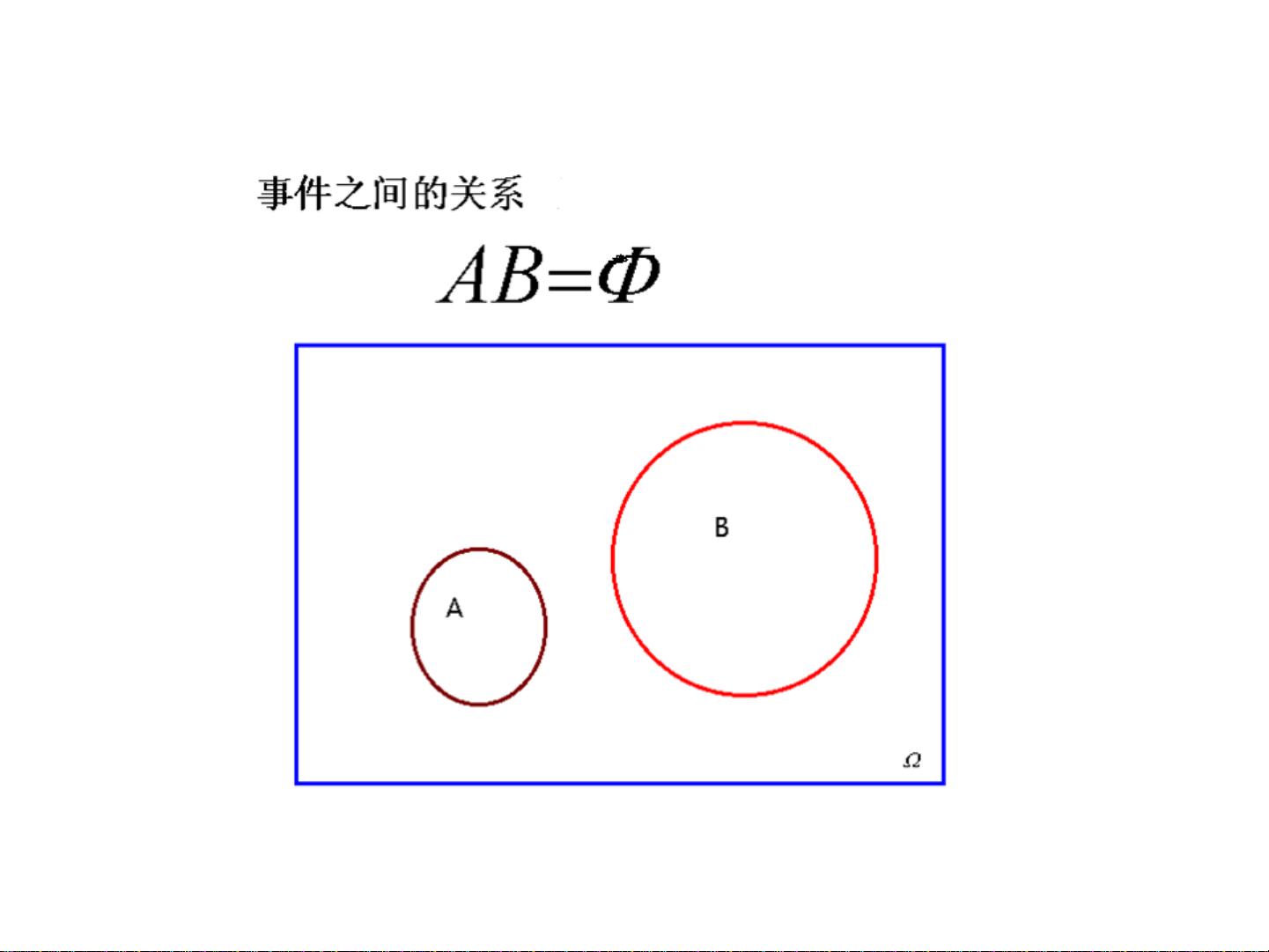
"这是一份来自武汉大学数学与统计学院概率论课程的课件，由教师邓爱姣讲授。课程包含概率论与数理统计的主要内容，如随机事件、随机变量、分布、数字特征、大数定律、中心极限定理、数理统计的基本概念、抽样分布、估计理论和假设检验等。考核方式为闭卷考试和平时成绩的结合，课程强调纪律，禁止上课使用手机，并提供答疑和邮件沟通的方式。" 在概率论课程中，我们首先会接触到随机事件与概率的概念。随机事件是指在一定条件下可能发生也可能不发生的事件，而概率则是描述这些随机事件发生的可能性大小。例如，掷一枚公平的骰子，每个面出现的概率是1/6。确定性现象与随机现象形成对比，前者的结果是必然的，后者则具有不确定性。 随机变量是概率论中的核心概念，它可以是离散的，如掷骰子的点数，也可以是连续的，如人的身高。每种随机变量都有特定的概率分布，比如二项分布、泊松分布、正态分布等，这些分布描述了变量取值的概率规律。 数字特征是衡量随机变量性质的重要工具，包括期望（均值）、方差、标准差等，它们能够刻画随机变量的集中趋势和波动程度。例如，期望表示随机变量的平均值，方差则反映了数值的分散程度。 概率极限定理，如大数定律和中心极限定理，是概率论中的基石。大数定律说明，当独立同分布的随机变量序列的样本数量足够大时，其算术平均趋向于期望值。中心极限定理则表明，大量独立随机变量的和，即使单个随机变量并不服从正态分布，它们的平均值也趋于正态分布。 数理统计部分，涵盖了基本概念，如总体、样本、抽样分布。参数估计和假设检验是统计学中的关键任务。参数估计是根据样本数据推断总体参数，如点估计和区间估计；假设检验则是通过统计检验来判断对总体参数的假设是否合理。 课程还涉及了一些高级统计分析方法，如回归分析用于探究两个或多个变量间的关联性，方差分析用于比较不同组别的差异，而正交实验设计法则是一种优化实验设计的统计方法，旨在减少实验次数并提高实验效率。 这门概率论课程旨在让学生理解和掌握处理随机现象的基本思想和方法，通过理论学习和实践应用，为后续的专业学习打下坚实的基础。学生需要遵守课程纪律，积极参与课堂活动，以获得全面的学习效果。