探索回溯算法：经典五例与决策树详解

本文主要介绍了五大常用经典算法之一——回溯算法，它是一种解决复杂问题的有效方法，尤其适用于那些存在多个可能解且需要尝试所有可能性的问题。在解决问题的过程中，回溯算法利用决策树的模型进行理解和应用。 在回溯算法中，核心步骤包括三个关键概念： 1. 路径（已做出的选择）：代表了解决问题过程中所走过的路径，即已选择的一系列决策或选项。例如，解决全排列问题时，路径就是排列好的数字序列。 2. 选择列表（当前可做的选择）：指在当前状态下可供选择的操作或选项，随着算法的推进，选择列表会不断缩小，直到达到结束条件。 3. 结束条件（无法再做选择的条件）：当到达决策树的叶子节点或者没有更多可选路径时，意味着问题解决完毕或者无解，算法停止。 回溯算法的通用框架，如给出的部分所示，使用递归来实现。`backtrack`函数定义了一个递归过程，每次迭代时，先从选择列表中选取一个选项（做选择），然后在递归调用中处理该选择带来的后续状态（深入决策树），最后在递归返回前撤销选择（恢复到上一步的状态），确保不会重复访问已探索过的选择。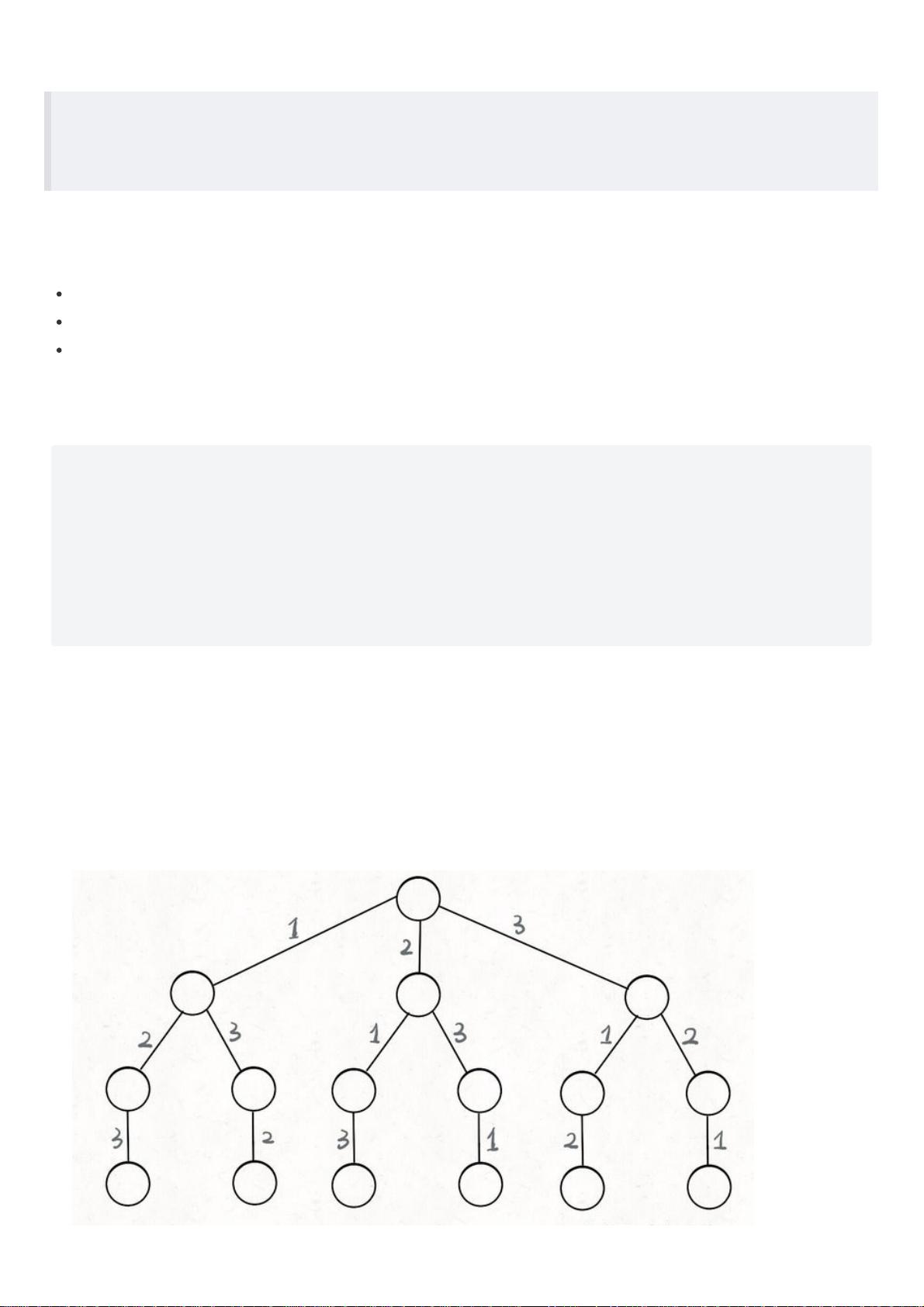 以全排列问题为例，算法通过穷举所有可能的排列组合，形成一个决策树，用户在每个节点上根据剩余可选数字做决策，直到选择列表为空或满足特定结束条件。这个过程展示了回溯算法的核心逻辑，即在有限的空间内尝试所有可能的路径，直到找到解决方案或者确认无解。 理解并掌握回溯算法对于学习和解决各种计算机科学问题至关重要，例如N皇后问题、八皇后问题等，都是经典的回溯算法应用场景。通过实践和深入理解这些概念，开发者能够更好地运用回溯思想来优化问题求解策略。