LIU et al.: OPPORTUNISTIC LINK OVERBOOKING FOR RESOURCE E FFICIENCY UNDER PER-FLOW SERVICE GUARANTEE 1771
Link
Management
Packets
Output
Packets
Input
New flow?
Yes
Flow
identification
No
Construct new packet queue
D elay s en s itive flo w s
Loss sensitive flows
Lo w prio rity flows
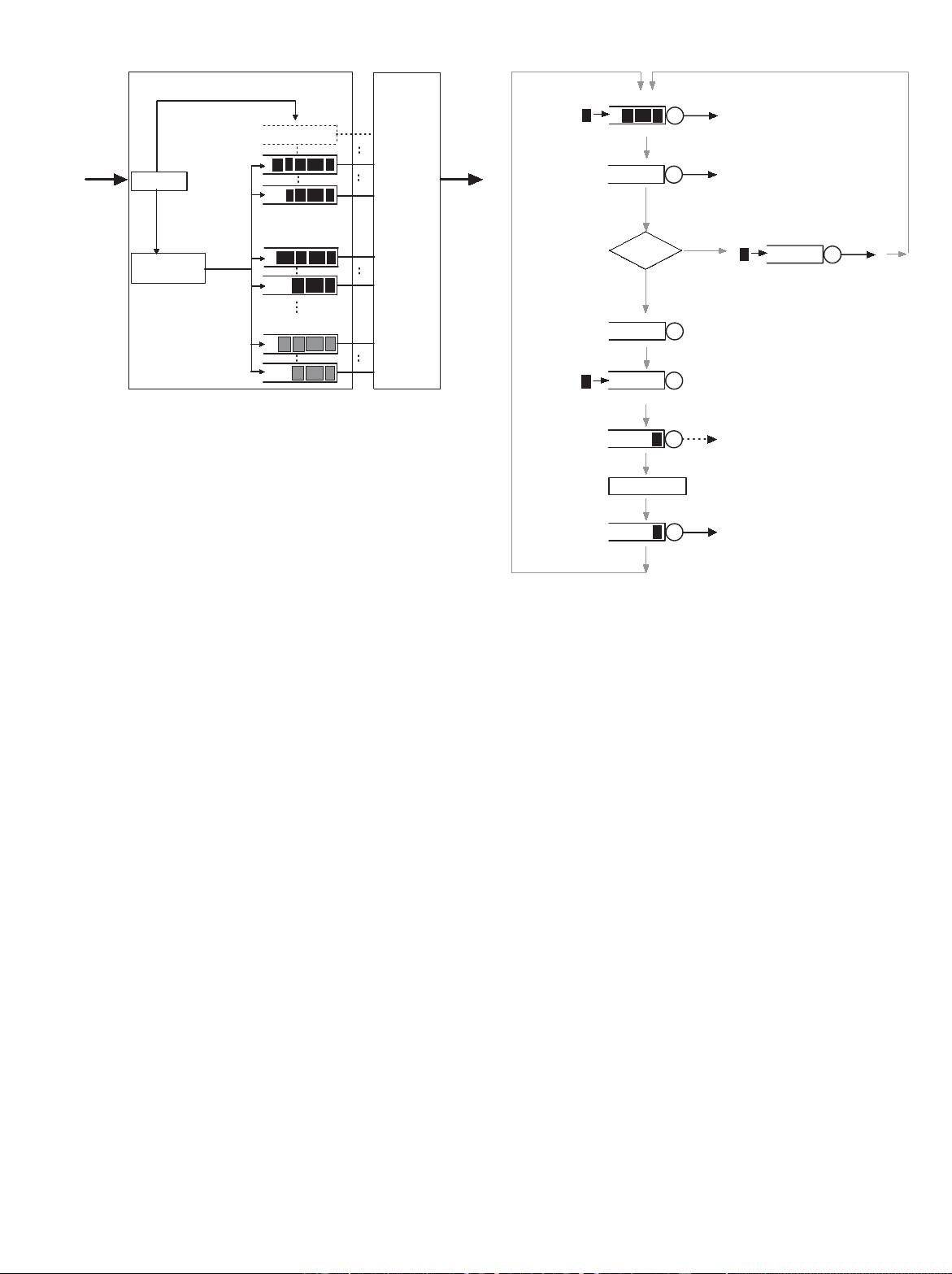
Fig. 1. Edge gatewa y adopting per-flow queueing.
measures are exhibited in Section V, and finally Section VI
concludes the paper.
II. O
PPORTUNISTIC LINK OVE RBOOKING SCHEME AND
ITS
QUEUEING MODEL
A. The OLO Overbooking Scheme
From the perspective of resource management, packet
queues and links are essential components of gateways, where
the incoming packets are buffered in the queue and cleared by
the link. As depicted in Fig. 1, the edge gateway we consider
adopts per-flow queueing policy [6], [24]. In the gateway, the
input packet streams are classified into different packet flows
by flow id entification and an isolated queue is maintained for
each flow. The flows can be divided into low priority flows and
high priority flows. The former, such as FTP or Email flows,
usually receives best effort service, having no stringent QoS
requirement, but often suffering bandwidth starvation if high
priority flows are heavy. The latter can be further classified as
delay-sensitive flows and loss-sensitive flows, which demand
service guarantee from the network and are the focus of this
paper.
The link management module is responsible for managing
the link of every packet flow according to the overbooking
scheme depicted in Fig. 2. Without loss of generality, in our
discussion we just focus on one of the packet queues (referred
as tagged queue hereafter). For a better understanding of our
scheme, the tagged packet queue can be regarded as having a
virtual server, which clears the flow’s packets through its link
and also controls the setting up or overbooking of this link.
Assume the packet arrival of the tagged flow is Poisson
process with rate 𝜆. The packet length 𝑏, measured with the
outgoing transmission time (i.e., service time) of the packet,
follows a general distribution with mean
¯
𝑏 (
¯
𝑏<∞), cumula-
tive distribution function (CDF) 𝐵(𝑥) and the corresponding
Laplace-Stieltjes transform (LST) is denoted by 𝑏
∗
(𝑠).
The Poisson assumption on packet arrivals can be justified
by the flow’s random behavior of packet generating, which is
caused by the new emerging features in the edge networks,
such as random sleep scheme, energy-aware traffic shaping
Link busy
Link id le
Link overbooked
Subsequent packet arriving
Packet queue
Server
R ec o ver th e link
Idle time > L
Link recovered
After setup time c
No
Yes
Subsequent packet arriving
Fig. 2. Demonstration of opportunistic link overbooking scheme on a tagged
packet queue.
and media transcoding, etc. Note that the receipt of a packet at
an edge gateway can be considered instantaneous, because the
bandwidth of an incoming link to an ingress edge gateway is
usually much higher than that of an outgoing link. The Poisson
assumptio n also allows us to obtain closed-form formulas that
can still give us enough insights on our scheme’s performance.
For a high priority flow, th e que ued packets are transmitted
through its quasi-dedicated link in First-In-First-Out (FIFO)
order. When the packet queue is emptied, the link becomes
idle; once the idle time exceeds the inactivity time 𝐿,the
server opportunistically overbooks the link to transmit packets
for a low priority flow. From the viewpoint of the high priority
flow, the server seems to take vacation. And then, when
the high priority flow’s subsequent packets start arriving, it
will take a setup time 𝑐 to recover this link and resume the
service. The preemptive task of this link is to guarantee the
high priority flow’s service. Only when this link is idle, it is
overbooked and allowed to temporarily carry a low priority
flow’s traffic to improve the efficiency, and we thus name it
as quasi-dedicated link.
The setup time is involved, because the system has to do
some operations to recover this link for the (high priority)
tagged queue. For example, in the ATM/MPLS networks,
recovering a link needs to restore a series of VPI/VCI config-
urations along the path and regain the original set of resources
[37]. The duration of setup time depends on the features of the
specific network, so we suppose 𝑐 is generally distributed with
mean value ¯𝑐 (¯𝑐<∞), probability density function (PDF)
𝑐(𝑥) and LST 𝑐
∗
(𝑠). Because the server takes vacation only
Authorized licensed use limited to: GUILIN UNIVERSITY OF ELECTRONIC TECHNOLOGY. Downloaded on June 24,2010 at 17:08:38 UTC from IEEE Xplore. Restrictions apply.









