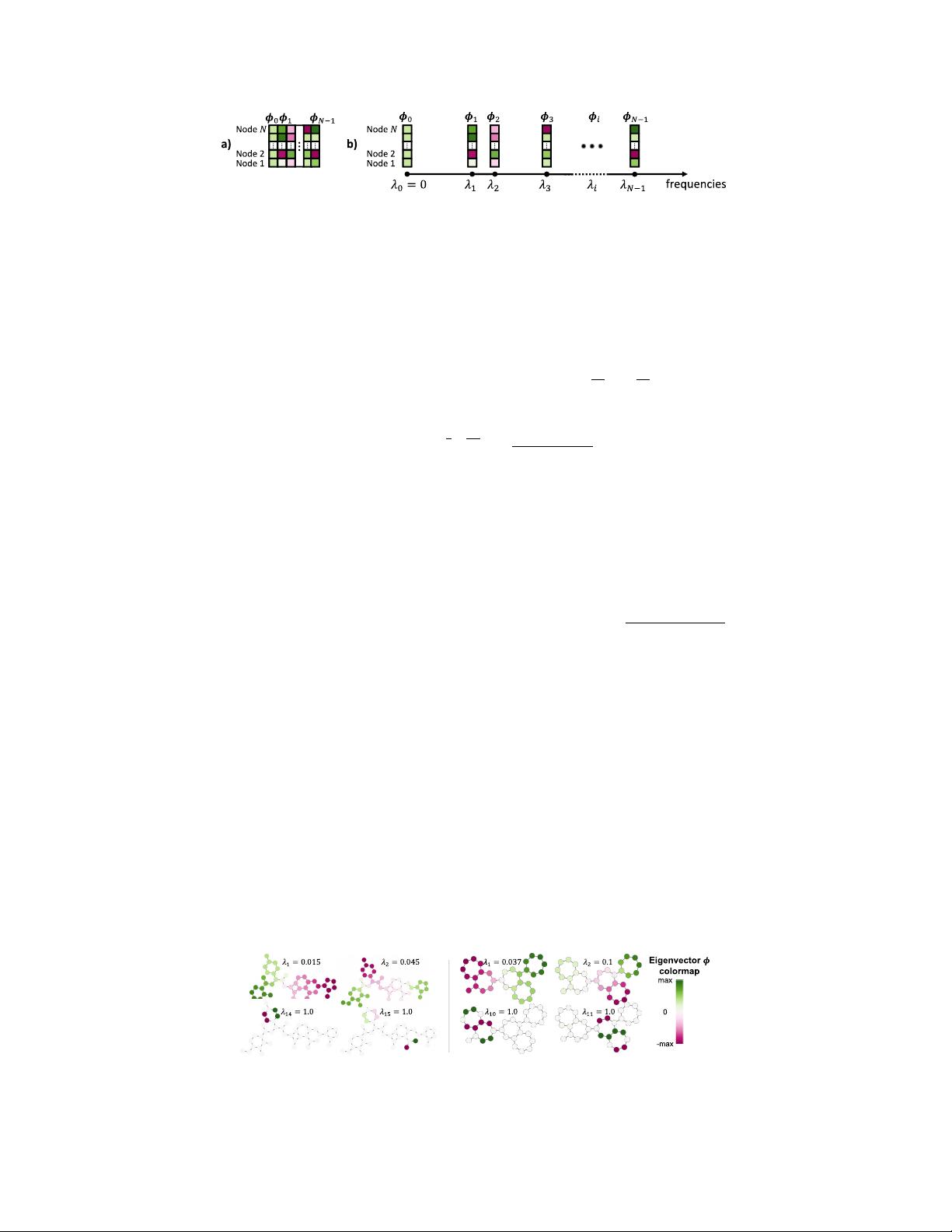
Figure 2: a) Standard view of the eigenvectors as a matrix. b) Eigenvectors
φ
i
viewed as vectors
positionned on the axis of frequencies (eigenvalues).
the Laplacian is a fundamental operator in physics and is notably used in Maxwell’s equations [
16
]
and the heat diffusion [6].
In electromagnetic theory, the (pseudo)inverse of the Laplacian, known in mathematics as the Green’s
function of the Laplacian [
9
], represents the electrostatic potential of a given charge. In a graph, the
same concept uses the pseudo-inverse of the Laplacian
G
and can be computed by its eigenfunctions.
See equation 1 , where
G(j
1
, j
2
)
is the electric potential between nodes
j
1
and
j
2
,
ˆ
φ
i
and
ˆ
λ
i
are
the i-th eigenvectors and eigenvalues of the symmetric Laplacian D
−1
2
LD
−1
2
, and D is the degree
matrix, and
ˆ
φ
i,j
the j-th row of the vector.
G(j
1
, j
2
) = d
1
2
j
1
d
−1
2
j
2
X
i>0
(
ˆ
φ
i,j
1
ˆ
φ
i,j
2
)
2
ˆ
λ
i
(1)
Further, the original solution of the heat equation given by Fourier relied on a sum of sines/cosines
known as a Fourier series [
7
]. As eigenvectors of the Laplacian are the analogue of these functions in
graphs, we find similar solutions. Knowing that heat kernels are correlated to random walks [
6
,
4
],
we use the interaction between two heat kernels to define in equation 2 the diffusion distance
d
D
between nodes
j
1
, j
2
[
6
,
10
]. Similarly, the biharmonic distance
d
B
was proposed as a better measure
of distances [28]. Here we use the eigenfunctions of the regular Laplacian L.
d
2
D
(j
1
, j
2
) =
X
k>0
e
−2tλ
i
(φ
i,j
1
− φ
i,j
2
)
2
, d
2
B
(j
1
, j
2
) =
X
i>0
(φ
i,j
1
− φ
i,j
2
)
2
λ
2
i
(2)
There are a few things to note from these equations. Firstly, they highlight the importance of pairing
eigenvectors and their corresponding eigenvalues when supplying information about relative positions
in a graph. Secondly, we notice that the product of eigenvectors is proportional to the electrostatic
interaction, while the subtraction is proportional to the diffusion and biharmonic distances. Lastly,
there is a consistent pattern across all 3 equations: smaller frequencies/eigenvalues are more heavily
weighted when determining distances between nodes.
2.1.3 Hearing the shape of a graph and its sub-structures
Another well-known property of eigenvalues is how they can be used to discriminate between different
graph structures and sub-structures, as they can be interpreted as the frequencies of resonance
of the graph. This led to the famous question about whether we can hear the shape of a drum
from its eigenvalues [
23
], with the same questions also applying to geometric objects [
12
] and 3D
molecules [
33
]. Various success was found with the eigenfunctions being used for partial functional
correspondence [
32
], algorithmic understanding geometries [
26
], and style correspondence [
12
].
Examples of eigenvectors for molecular graphs are presented in Figure 3.
Figure 3: Examples of eigenvalues
λ
i
and eigenvectors
φ
i
for molecular graphs. The low-frequency
eigenvectors
φ
1
, φ
2
are spread accross the graph, while higher frequencies, such as
φ
14
, φ
15
for the
left molecule or φ
10
, φ
11
for the right molecule, often resonate in local structures.
4










