经验模态分解与希尔伯特黄变换在非线性时间序列分析中的应用

5星 · 超过95%的资源需积分: 50 142 浏览量更新于2024-07-26 收藏 2.41MB PDF 举报

"经验模态分解和希尔伯特黄变换是两种在信号处理和数据分析领域中重要的方法，特别适用于非线性和非平稳时间序列的分析。经验模态分解（Empirical Mode Decomposition, EMD）是由Norden E. Huang等人在1998年提出的一种数据驱动的信号分解技术，它能够将复杂的时间序列分解为一系列内在模态函数（Intrinsic Mode Function, IMF）。这种方法无需预先假设信号的模型，因此对于非线性、非高斯以及非平稳信号的处理具有很大的优势。希尔伯特黄变换（Hilbert-Huang Transform, HHT）则是在EMD的基础上，通过构造希尔伯特变换来获取每个IMF的瞬时频率和振幅，从而提供了一种分析非平稳信号动态特性的工具。HHT不仅揭示了信号的时间演化，还提供了其频谱信息，因此在许多科学和工程领域中都有广泛应用，如地球科学、生物医学、机械故障诊断、金融数据分析等。在文章‘The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis’中，作者详细介绍了EMD的原理和步骤，包括迭代过程中的平均包络线定义、IMF的提取条件以及残差的确定等。同时，他们阐述了如何结合希尔伯特变换构建希尔伯特谱（Hilbert Spectrum），用于展示信号的瞬时频率和振幅变化，进一步展示了这种方法在分析非线性、非平稳信号上的优越性。此外，文章引用了相关的参考文献，表明了这一方法的理论基础和实际应用价值。读者可以通过提供的链接获取全文，或者设置电子邮件提醒服务以关注该领域的最新研究进展。" 这篇摘要涵盖了经验模态分解（EMD）和希尔伯特黄变换（HHT）的基本概念、应用场景以及它们在非线性、非平稳时间序列分析中的作用。通过这些方法，科学家和工程师可以更好地理解和解析复杂信号的行为，从而在各种实际问题中找到有价值的见解。

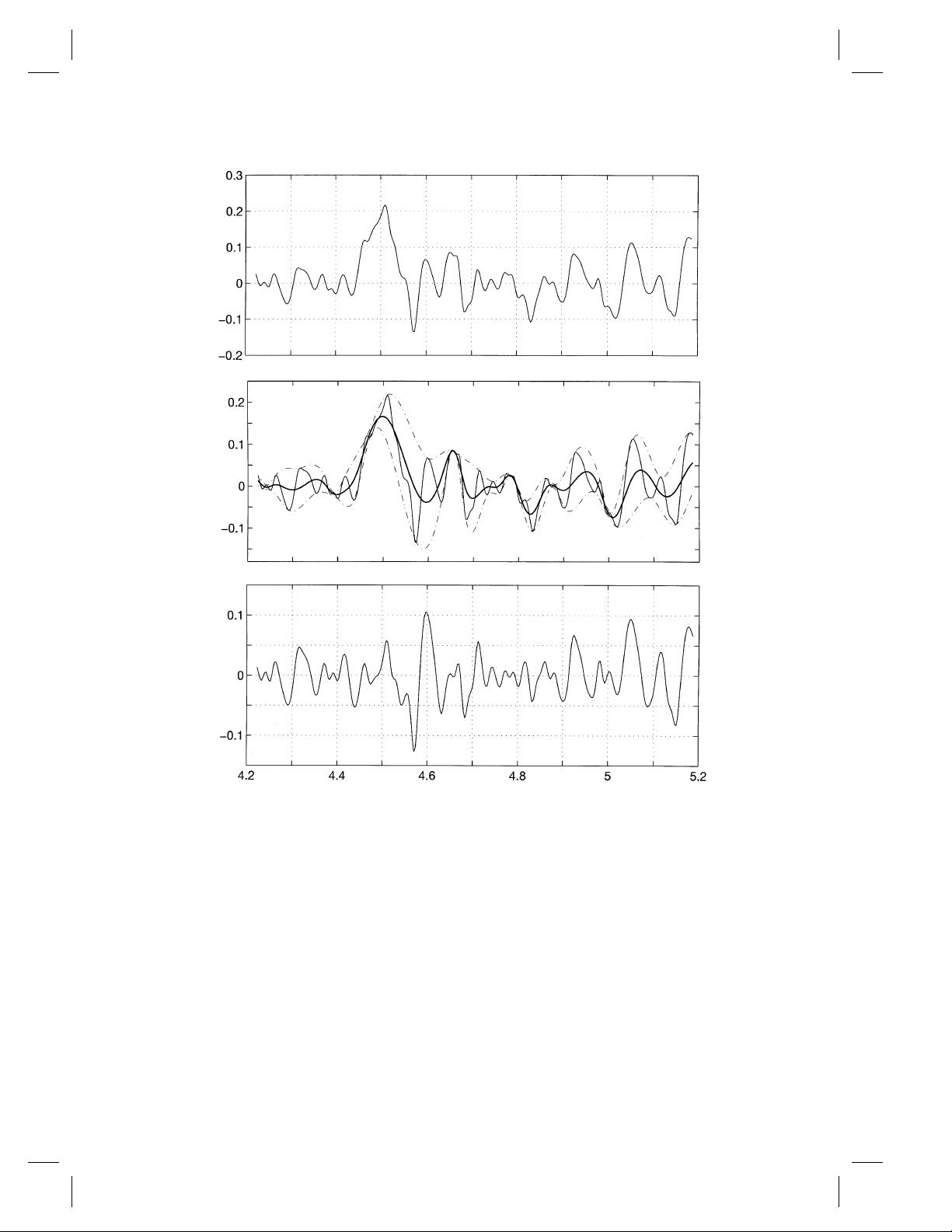
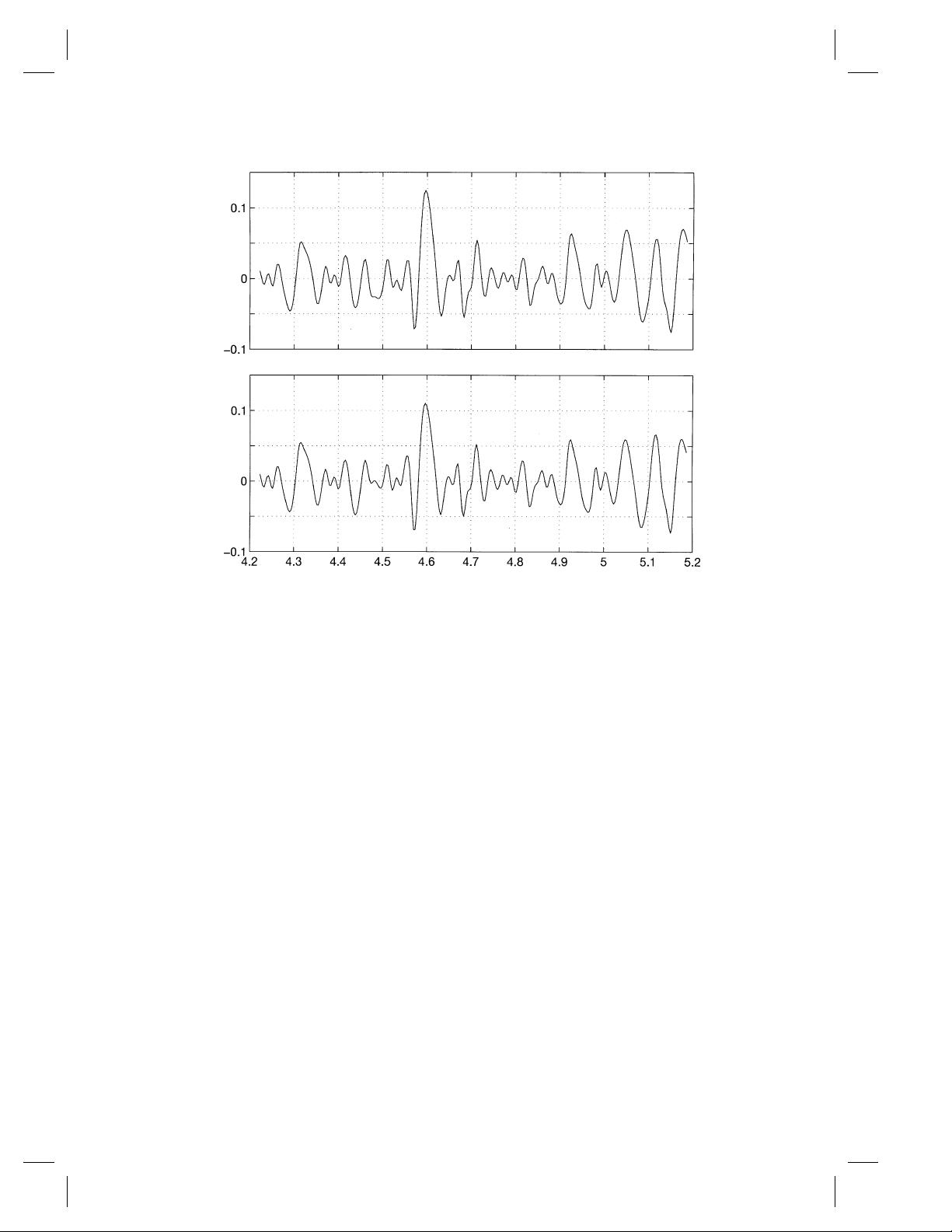
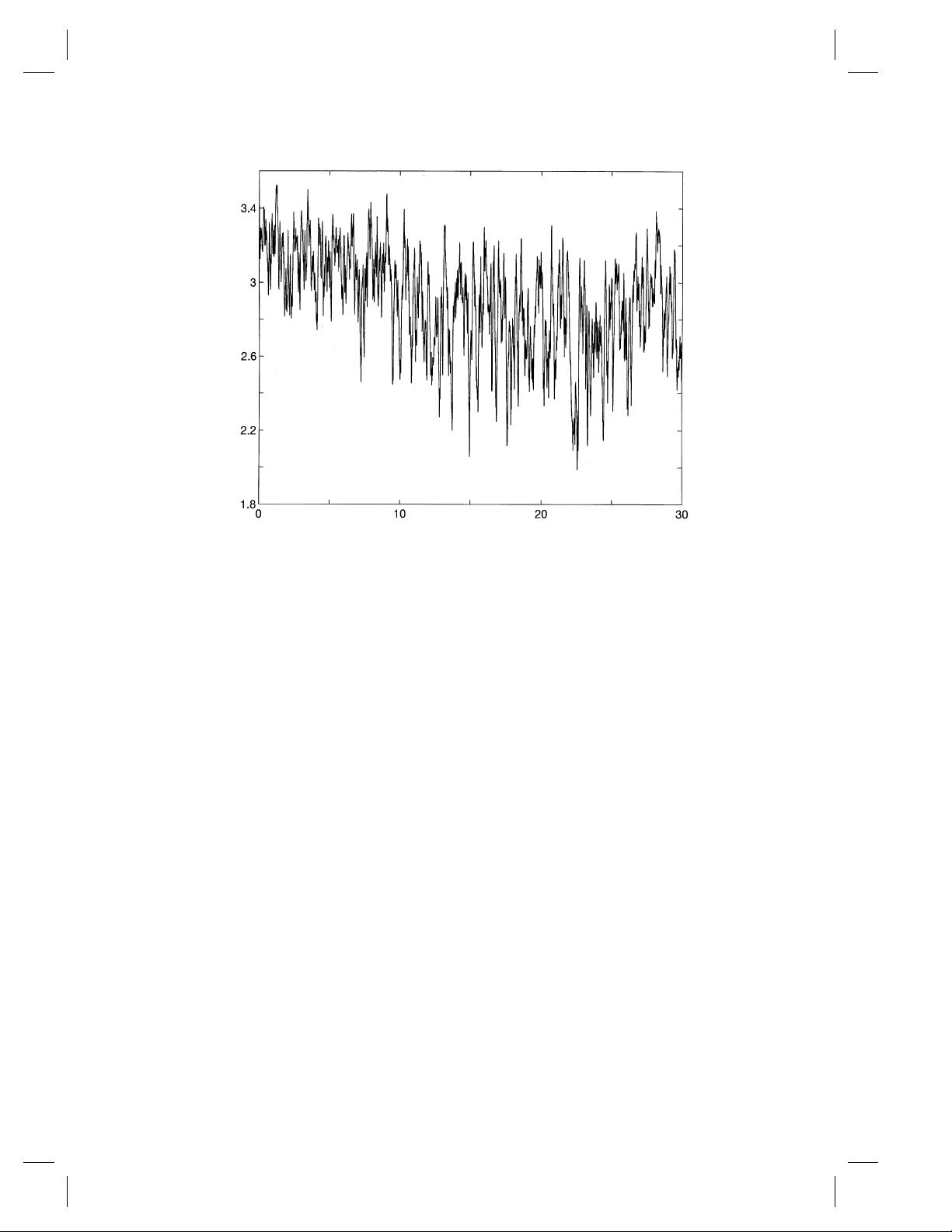
Nonlinear and non-stationary time series analysis 917

was not emphasized either for convenience, or for lack of a more precise frequency

deﬁnition. The second type is less familiar, but it is also a common phenomenon: if

the frequency changes from time to time within a wave its proﬁle can no longer be

a simple sine or cosine function. Therefore, any wave-proﬁle deformation from the

simple sinusoidal form implies the intrawave frequency modulation. In the past such

phenomena were treated as harmonic distortions. We will show in detail later that

most such deformations are better viewed as intrawave frequency modulation, for

the intrawave frequency modulation is more physical.

In order to use this unique deﬁnition of instantaneous frequency, we have to reduce

an arbitrary data set into IMF components from which an instantaneous frequency

value can be assigned to each IMF component. Consequently, for complicated data,

we can have more than one instantaneous frequency at a time locally. We will intro-

duce the empirical mode decomposition method to reduce the data into the needed

IMFs.

5. The empirical mode decomposition method: the sifting process

Knowing the well-behaved Hilbert transforms of the IMF components is only the

starting point. Unfortunately, most of the data are not IMFs. At any given time, the

data may involve more than one oscillatory mode; that is why the simple Hilbert

transform cannot provide the full description of the frequency content for the general

data as reported by Long et al. (1995). We have to decompose the data into IMF

components. Here, we will introduce a new method to deal with both non-stationary

and nonlinear data by decomposing the signal ﬁrst, and discuss the physical mean-

ing of this decomposition later. Contrary to almost all the previous methods, this

new method is intuitive, direct, a posteriori and adaptive, with the basis of the

decomposition based on, and derived from, the data.

The decomposition is based on the assumptions: (1) the signal has at least two

extrema—one maximum and one minimum; (2) the characteristic time scale is

deﬁned by the time lapse between the extrema; and (3) if the data were totally

devoid of extrema but contained only inﬂection points, then it can be diﬀerenti-

ated once or more times to reveal the extrema. Final results can be obtained by

integration(s) of the components.

The essence of the method is to identify the intrinsic oscillatory modes by their

characteristic time scales in the data empirically, and then decompose the data

accordingly. According to Drazin (1992), the ﬁrst step of data analysis is to examine

the data by eye. From this examination, one can immediately identify the diﬀerent

scales directly in two ways: by the time lapse between the successive alternations of

local maxima and minima; and by the time lapse between the successive zero cross-

ings. The interlaced local extrema and zero crossings give us the complicated data:

one undulation is riding on top of another, and they, in turn, are riding on still other

undulations, and so on. Each of these undulations deﬁnes a characteristic scale of the

data; it is intrinsic to the process. We have decided to adopt the time lapse between

successive extrema as the deﬁnition of the time scale for the intrinsic oscillatory

mode, because it not only gives a much ﬁner resolution of the oscillatory modes, but

also can be applied to data with non-zero mean, either all positive or all negative

values, without zero crossings. A systematic way to extract them, designated as the

sifting process, is described as follows.

Proc. R. Soc. Lond. A (1998)

on December 22, 2012rspa.royalsocietypublishing.orgDownloaded from

Nonlinear and non-stationary time series analysis 919

(a)

(b)

wind speed (ms

–1

)wind speed (ms

–1

)

Time (s)

Figure 4. Illustration of the eﬀects of repeated sifting process: (a) after one more sifting of the

result in ﬁgure 3c, the result is still asymmetric and still not a IMF; (b) after three siftings, the

result is much improved, but more sifting needed to eliminate the asymmetry. The ﬁnal IMF is

shown in ﬁgure 2 after nine siftings.

the data in the thin solid line, the upper and the lower envelopes in the dot-dashed

lines, and their mean in the thick solid line, which bisects the data very well; and ﬁg-

ure 3c gives the diﬀerence between the data and the local mean as in equation (5.1)).

Ideally, h

should be an IMF, for the construction of h

described above seems to

have been made to satisfy all the requirements of IMF. In reality, however, overshoots

and undershoots are common, which can also generate new extrema, and shift or

exaggerate the existing ones. The imperfection of the overshoots and undershoots

can be found at the 4.6 and 4.7 s points in ﬁgure 3b. Their eﬀects, however, are

not direct, for it is the mean, not the envelopes, that will enter the sifting process.

Nevertheless, the problem is real. Even if the ﬁtting is perfect, a gentle hump on

a slope can be ampliﬁed to become a local extremum in changing the local zero

from a rectangular to a curvilinear coordinate system. An example can be found for

the hump between the 4.5 and 4.6 s range in the data in ﬁgure 3a. After the ﬁrst

round of sifting, the hump becomes a local maximum at the same time location as

in ﬁgure 3c. New extrema generated in this way actually recover the proper modes

lost in the initial examination. In fact, the sifting process can recover low-amplitude

riding waves with repeated siftings.

Still another complication is that the envelope mean may be diﬀerent from the

true local mean for nonlinear data; consequently, some asymmetric wave forms can

still exist no matter how many times the data are sifted. We have to accept this

approximation as discussed before.

Proc. R. Soc. Lond. A (1998)

on December 22, 2012rspa.royalsocietypublishing.orgDownloaded from

920 N. E. Huang and others

Other than these theoretical diﬃculties, on the practical side, serious problems of

the spline ﬁtting can occur near the ends, where the cubic spline ﬁtting can have

large swings. Left by themselves, the end swings can eventually propagate inward and

corrupt the whole data span especially in the low-frequency components. We have

devised a numerical method to eliminate the end eﬀects; details will be given later.

At any rate, improving the spline ﬁtting is absolutely necessary. Even with these

problems, the sifting process can still extract the essential scales from the data.

The sifting process serves two purposes: to eliminate riding waves; and to make

the wave-proﬁles more symmetric. Toward this end, the sifting process has to be

repeated more times. In the second sifting process, h

is treated as the data, then

− m

= h

. (5.2)

Figure 4a shows the much improved result after the second sifting, but there are still

local maxima below the zero line. After another sifting, the result is given in ﬁgure 4b.

Now all the local maxima are positive, and all the local minima are negative, but

many waves are still asymmetric. We can repeat this sifting procedure k times, until

is an IMF, that is

1(k−1)

− m

= h

, (5.3)

the result is shown in ﬁgure 2 after nine siftings. Then, it is designated as

= h

, (5.4)

the ﬁrst IMF component from the data.

As described above, the process is indeed like sifting: to separate the ﬁnest local

mode from the data ﬁrst based only on the characteristic time scale. The sifting

process, however, has two eﬀects: (a) to eliminate riding waves; and (b) to smooth

uneven amplitudes.

While the ﬁrst condition is absolutely necessary for the instantaneous frequency to

be meaningful, the second condition is also necessary in case the neighbouring wave

amplitudes have too large a disparity. Unfortunately, the second eﬀect, when carried

to the extreme, could obliterate the physically meaningful amplitude ﬂuctuations.

Therefore, the sifting process should be applied with care, for carrying the process

to an extreme could make the resulting IMF a pure frequency modulated signal of

constant amplitude. To guarantee that the IMF components retain enough physical

sense of both amplitude and frequency modulations, we have to determine a criterion

for the sifting process to stop. This can be accomplished by limiting the size of the

standard deviation, SD, computed from the two consecutive sifting results as

SD =

t=0

|(h

1(k−1)

(t) −h

(t))|

1(k−1)

(t)

. (5.5)

A typical value for SD can be set between 0.2 and 0.3. As a comparison, the two

Fourier spectra, computed by shifting only ﬁve out of 1024 points from the same

data, can have an equivalent SD of 0.2–0.3 calculated point-by-point. Therefore, a

SD value of 0.2–0.3 for the sifting procedure is a very rigorous limitation for the

diﬀerence between siftings.

Overall, c

should contain the ﬁnest scale or the shortest period component of the

signal. We can separate c

from the rest of the data by

X(t) −c

= r

. (5.6)

Proc. R. Soc. Lond. A (1998)

on December 22, 2012rspa.royalsocietypublishing.orgDownloaded from

剩余96页未读，继续阅读

xinhai475888622

粉丝: 0
资源: 2

经验模态分解与希尔伯特黄变换在非线性时间序列分析中的应用

EMD-希尔伯特黄变换

经验模态分解程序代码

基于EMD分解·和希尔伯特变换(HHT)的完整 MATLAB代码.rar

经典模态分解，希尔伯特黄变换

深入理解经验模态分解与希尔伯特黄变换

经验模态分解_hilberthuang_publicd3w_经验模态分解_希尔伯特变化_希尔伯特黄变换_

经验模态分解及希尔伯特-黄变换的MATLAB程序

经验模态分解（希尔伯特-黄变换）实现心电信号去噪附matlab代码+仿真结果和运行方法+仿真结果和运行方法.zip

集成变分模态分解和希尔伯特-黄变换的结构振动时频提取模型.docx

EMD经验模态分解与希尔伯特变换的MATLAB实现

最新资源