最小生成树算法详解：Kruskal与Prim方法

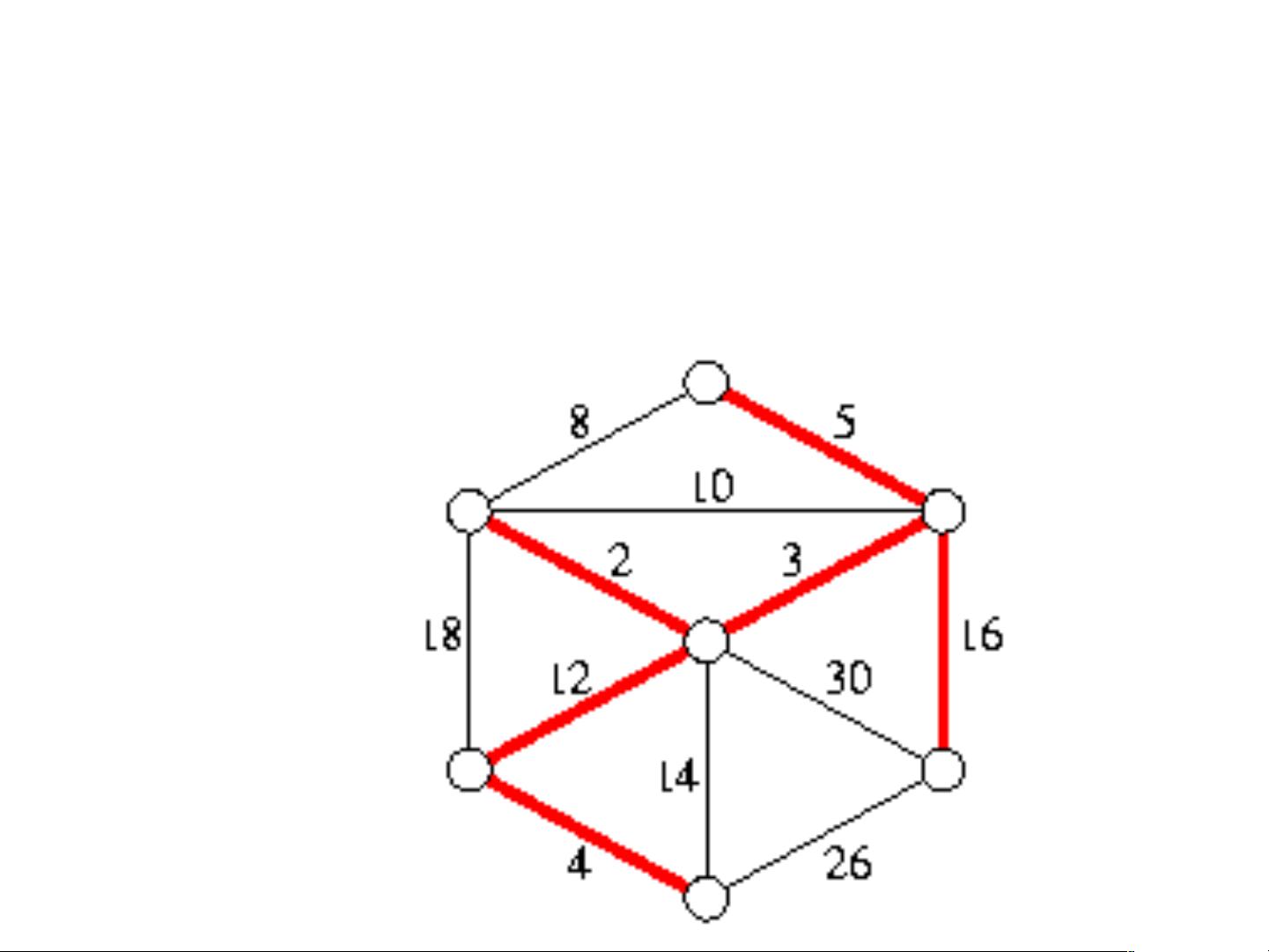
最小生成树是算法图论中的一个重要概念，用于解决在一个加权连通图中找到一棵边权和尽可能小的树的问题。这个概念在计算机科学和信息技术领域有着广泛的应用，尤其是在网络设计、数据压缩和优化问题中。 最小生成树问题的核心目标是构建一棵包含所有节点的树，使得边的总权重达到最小。通常假设图中不存在相等权重的边，以避免复杂性。在解决这个问题时，有两种主要的方法： 1. Kruskal算法： - Kruskal算法由约瑟夫·克鲁斯卡尔提出，它按照边的权重从小到大排序，然后依次选择没有形成环的边加入到生成树中。这个过程确保了生成树是连通的且边权和最小。 - 证明其正确性通常涉及到反证法，如果存在不在最小生成树中的安全边，可以通过替换使其权值变得更小，从而导致矛盾。 2. Prim算法： - Prim算法由查尔斯·埃里克·普里姆提出，尽管最初是由扬尼克在1930年独立发现。Prim算法采用贪心策略，从一个已知的顶点开始，逐步扩展树直到覆盖所有节点。它通过一个最小堆来存储未加入树的顶点到树中所有顶点的距离，每次都选择最近的那个顶点，从而添加一条安全边。 - 这种算法保证了每次选择的边都是当前状态下距离树最近的，因此也是最优的。 除了这两种经典算法，还提到了Boruvka算法，这是另一种早期的最小生成树算法，由阿尔弗雷德·博鲁娃克在1926年提出。Boruvka算法通过同时考虑所有连通分量的'领导者'，在多轮迭代中合并较小的分量，每次迭代后更新边的安全边权，最终达到最小生成树。这种方法的时间复杂度为O(E log V)，其中E表示边的数量，V表示顶点的数量。 无论是Kruskal还是Prim，它们都强调了最小生成树的独特性质，即不形成环，并保证找到的是全局最优解。理解这些算法不仅有助于解决实际问题，还能加深对图论和算法分析的基础知识掌握。学习和应用最小生成树算法是编程和信息技术专业人员必备的技能，特别是参加信息学竞赛或者处理复杂网络结构时。参考书《算法艺术与信息学竞赛》提供了详细的理论背景和实践指导，对于想要深入学习这个主题的学生和工程师来说是一份宝贵的资源。