张量分解详解：CPD与Tucker分解

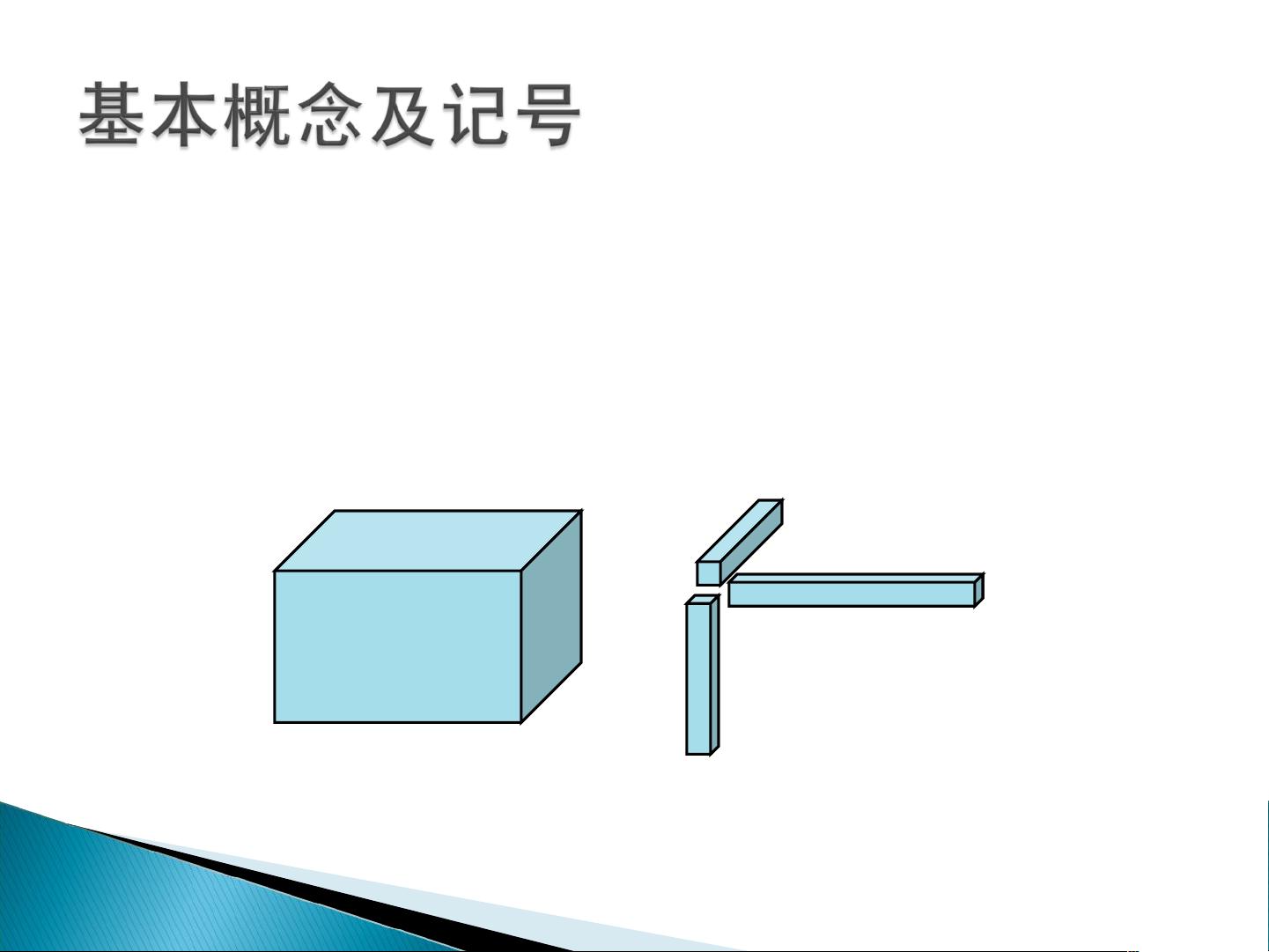
"张量分解讲义" 在数学和计算领域，张量是一个多维数组，它不仅用于表示向量和矩阵，还能表示更复杂的数据结构，尤其在图像处理和计算机视觉中发挥着重要作用。张量的阶数表示其维度数量，例如一阶张量是向量，二阶张量是矩阵，三阶及以上是高阶张量。张量空间是由多个向量空间的基底外积形成的，其中每个向量空间对应张量的一个模式。 对于张量的分解，有两种主要方法：CP分解（Canonical Polyadic Decomposition，CPD）和Tucker分解。CP分解是一种将高阶张量表示为一系列向量乘积的形式，类似于矩阵的奇异值分解。它将张量表示为： \[ X = \sum_{r=1}^R \lambda_r \mathbf{a}_r^{(1)} \otimes \mathbf{a}_r^{(2)} \otimes \cdots \otimes \mathbf{a}_r^{(N)} \] 其中，\( R \) 是秩，\( \lambda_r \) 是系数，\( \mathbf{a}_r^{(n)} \) 是与张量模式 \( n \) 相关的向量，\( \otimes \) 表示外积。CP分解在处理稀疏或低秩张量时特别有用，因为它可以减少数据的存储需求并提供结构化的解释。 另一方面，Tucker分解是将张量分解为一个核心张量和一系列因子矩阵的乘积，可以表示为： \[ X = G \times_1 U^{(1)} \times_2 U^{(2)} \times_3 \cdots \times_N U^{(N)} \] 其中，\( G \) 是核心张量，\( U^{(n)} \) 是与模式 \( n \) 相关的因子矩阵，\( \times_n \) 表示沿着第 \( n \) 模式的乘积。Tucker分解保留了张量的多维结构，并且通常用于数据分析和降维。 张量分解在机器学习、信号处理、图像分析等领域有广泛的应用。例如，在图像处理中，高阶张量可以表示多通道图像，通过分解可以提取特征并进行压缩。此外，张量分解也可用于推荐系统，通过对用户-物品交互的高阶关系进行建模，以提供更精确的个性化推荐。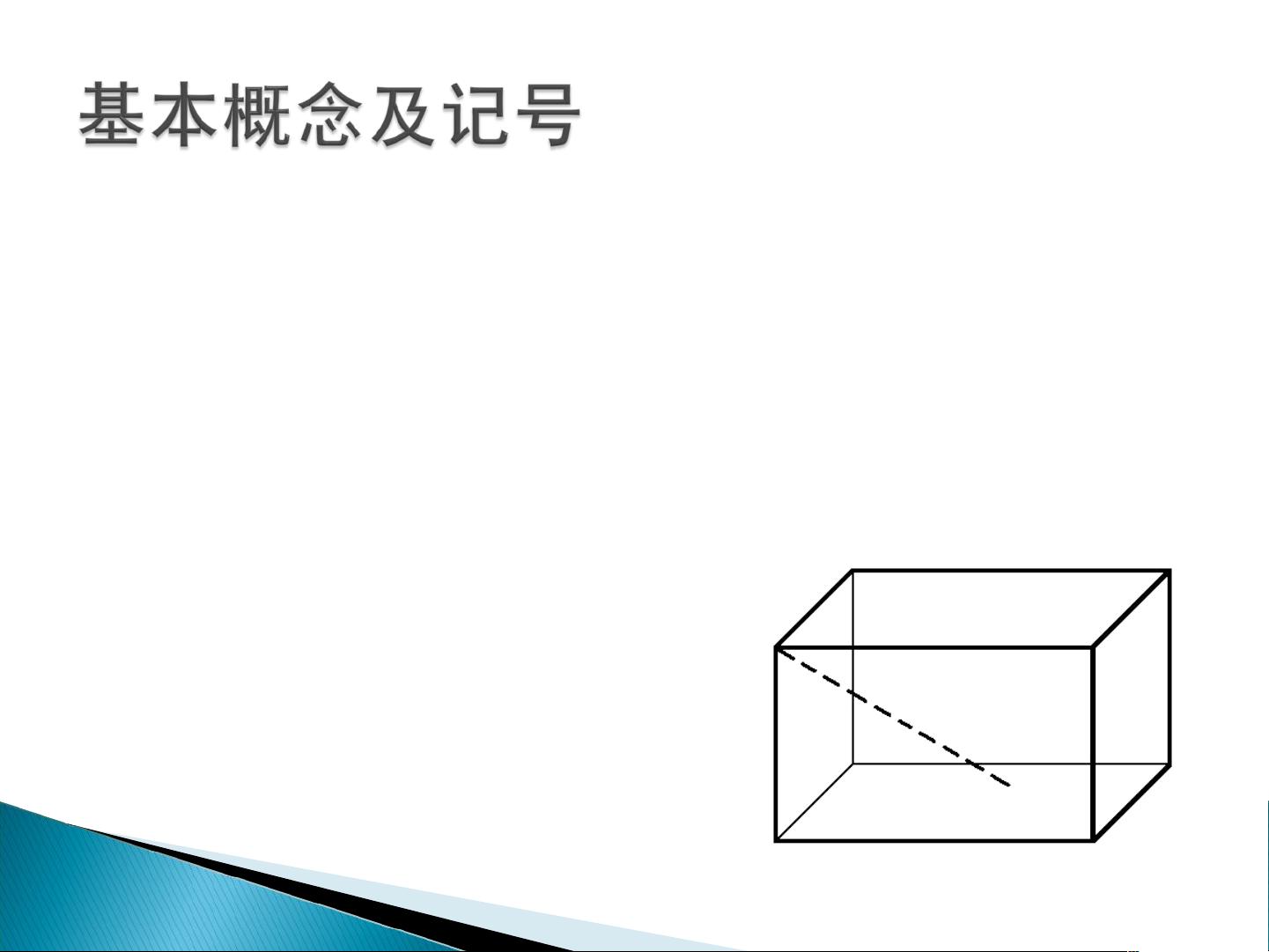 张量的其他重要概念包括纤维（对应于特定模式下的线性子空间）、切片（张量的二维子集，如水平切片、侧面切片和正面切片）以及张量的内积和范数，它们在计算张量的相似性和距离时起到关键作用。张量的秩定义了构成张量的最小向量乘积的数量，而对称性和超对称性则描述了张量在下标重新排列时的性质。最后，张量的展开（matricization）是将张量转换为矩阵的过程，便于使用传统的矩阵运算。 展开操作包括沿着不同模式展开成矩阵，如沿着模式1的展开 \( X(1) \)，这有助于将张量问题转化为矩阵问题，进而利用矩阵理论的丰富工具进行分析和计算。张量的这些基本概念和分解方法为理解和处理复杂数据提供了强大的数学工具。