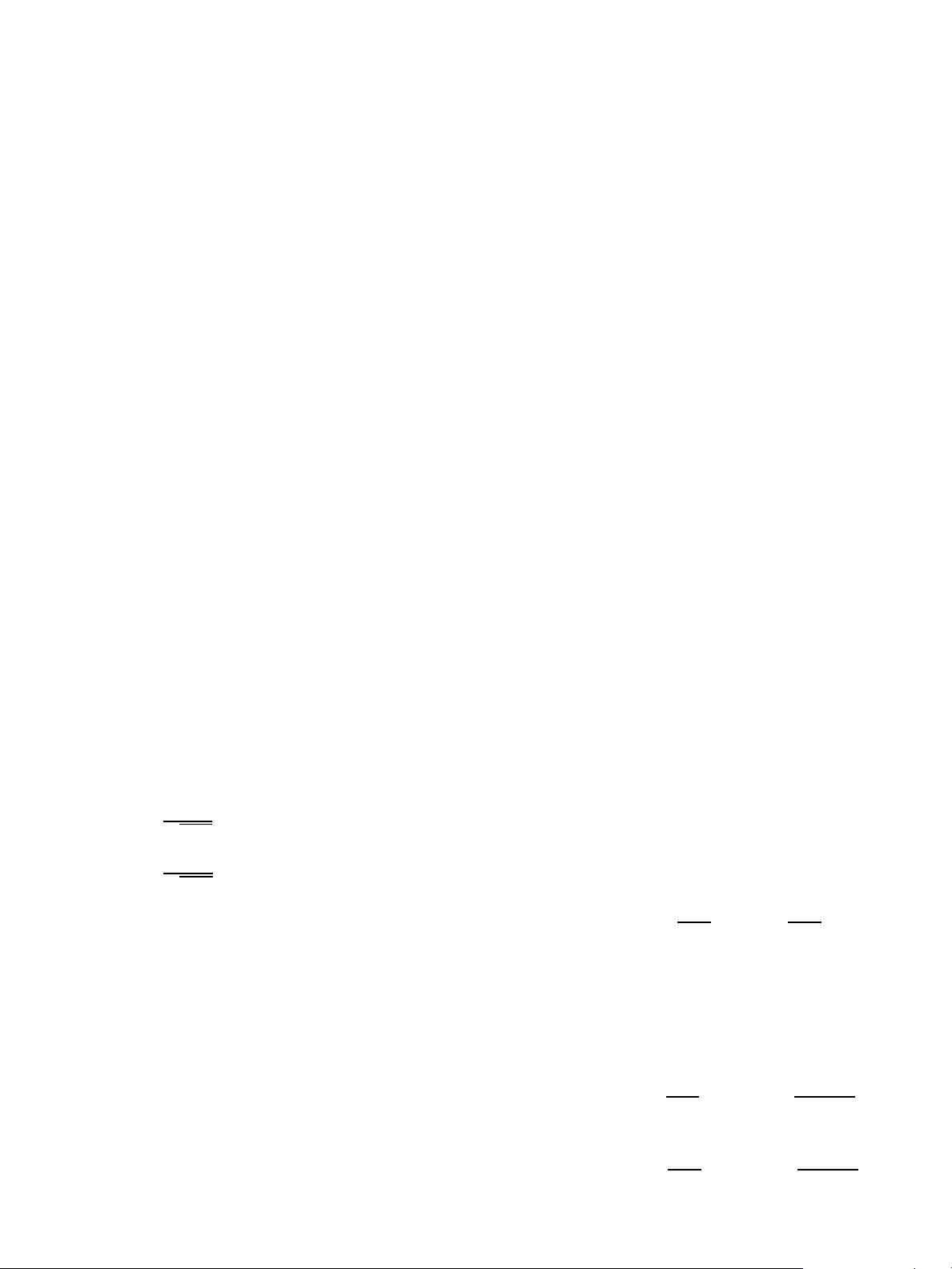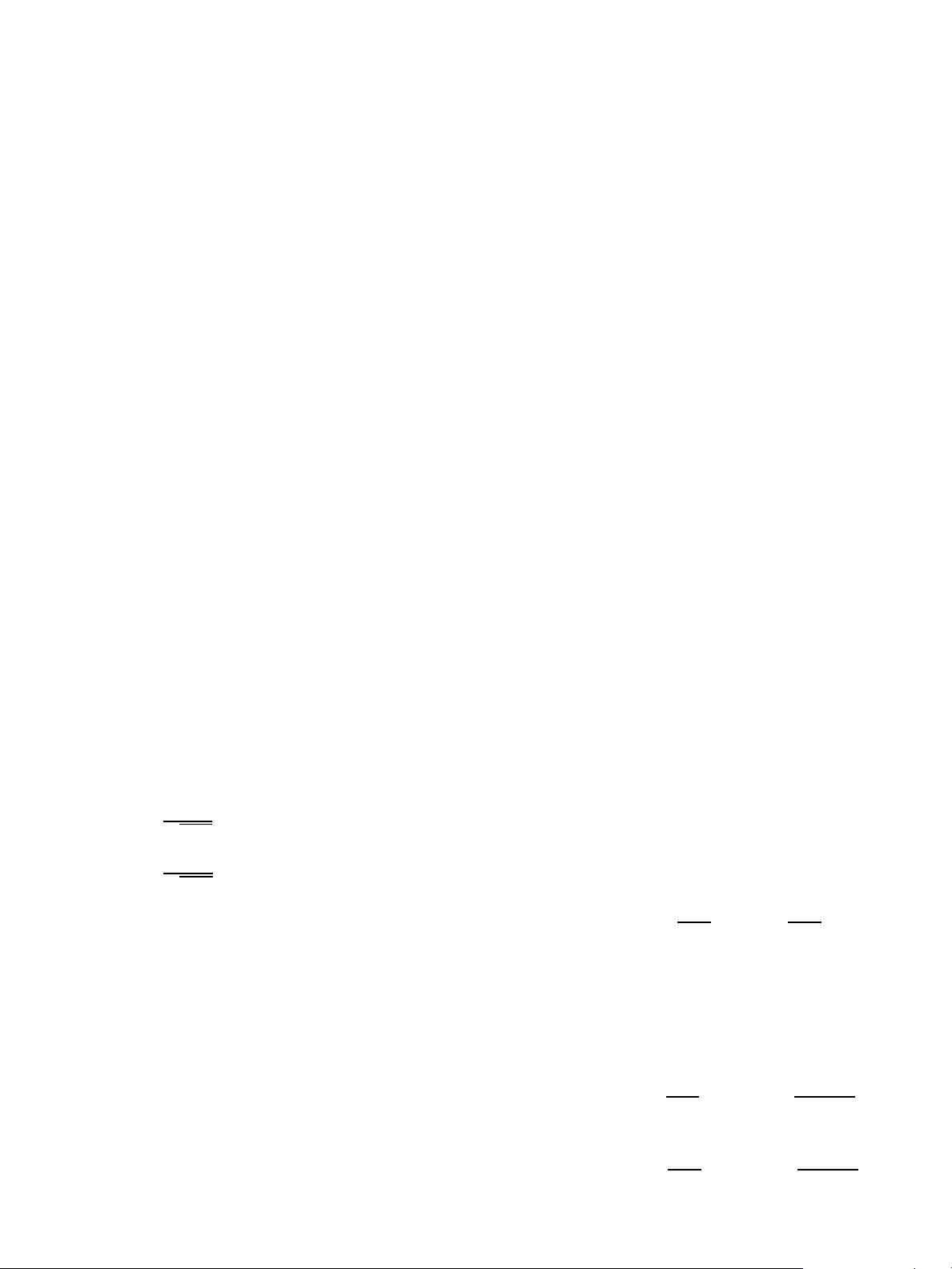
74 IEEE SYSTEMS JOURNAL, VOL. 11, NO. 1, MARCH 2017
Denoting y =[y
1
,y
2
,...,y
K
]
T
,wehave
y = HWx + n (2)
where H =[h
T
1
, h
T
2
,...,h
T
K
]
T
is the downlink channel ma-
trix, W =[w
1
, w
2
,...,w
K
] is the precoding matrix, x =
[x
1
,x
2
,...,x
K
]
T
is the transmit signal vector satisfying
E{xx
H
} = I
K
, and the precoded signal s = Wx satisfies the
power constrain E{s
H
s}≤P .
In Fig. 1 we can easily find out that, in a multiuser trans-
mission system, some users are distributed far away from
each other, while some users may be close to each other. For
instance, users 5 and 6 are located very close, and severe IUI
exists between them. In this case, there is a need for inter-
ference control; other w ise, the performance of the multiuser
transmission system will degrade significantly. Since precoding
is one of the key techniques to control the interference in
downlink transmission schemes, proper design of W becomes
very important.
B. Channel Model
Precoding design is based on the practical channel state of
the millimeter-wave massive MIMO system. Here, we adopt
the spatial multipath channel model a nd write the downlink
physical channel vector of user i as [18]
h
i
= β
i,0
a
t
(Ω
i,0
)+
N
p
l=1
β
i,l
a
t
(Ω
i,l
) (3)
where β
i,0
and β
i,l
are the path factors of the line-of-sight
(LOS) and non line-of-sight (NLOS) paths, respectively; Ω
i,j
=
(θ
i,j
,ϕ
i,j
) represents the angles of departure (AoDs) of the jth
path; θ
i,j
and ϕ
i,j
are the downtilt and the azimuth, respec-
tively.
1
a
t
(Ω) ∈ C
1×N
t
is the steering vector of UPA antenna
array with AoD Ω=(θ, ϕ), and it can be written as [12]
a
t
(Ω) = a
t
(θ, ϕ)=a
(v)
t
(Θ) ⊗ a
(h)
t
(Ξ)
a
(v)
t
(Θ) =
1
N
(v)
t
1,e
−j2πΘ
,...,e
−j2π
N
(v)−1
t
Θ
a
(h)
t
(Ξ) =
1
N
(h)
t
1,e
−j2πΞ
,...,e
−j2π
N
(h)−1
t
Ξ
(4)
where Θ=d
(v)
t
/λ sin θ, Ξ=d
(h)
t
/λ cos θ sin ϕ, N
t
= N
(v)
t
×
N
(h)
t
, N
(v)
t
and N
(h)
t
represent the number of UPA rows and
columns, d
(v)
t
and d
(h)
t
are the distances between two adjacent
antenna elements in a row and a column, and λ is the carrier
waveleng th. As mentio ned earlier, for millimeter-wave systems,
the p rimary existing broadcast path is LOS, and NLOS suffers
from significant path loss; therefore, |β
i,0
||β
i,l
| for l ≥ 1.
In the remainder of this paper, we neglect the NLOS paths and
adopt the single-path model used in [14]. The physical channel
model (3) becomes
h
i
≈ β
i,0
a
t
(Ω
i,0
)=β
i,0
a
t
(θ
i,0
,ϕ
i,0
). (5)
1
We use block fading to model the channel, where the channel fading
coefficients keep constant during the transmission of a data block and changes
independently (randomly) in another block.
The following discussion will be based on this single-path
expression. Since the NLOS paths still exist in pr actical
environment, we make detailed analysis about the multipath
propagation scenario in corresponding sections.
III. B
ASICS ON BEAMSPACE
This section introduces some basic information about
beamspace that will be needed in the following sections. In
general, beamspace transformation is a powerful mathematical
tool for massive MIMO, which enables us to look at the
LOS millimeter-wave channels in the so-called beamspace
perspective.
Considering the single antenna equipment of user i,the
beamspace transformation of its downlink channel vector can
be expressed as [19]
˜
h
i
= h
i
U (6)
where
˜
h
i
∈ C
1×N
t
is referred to as beamspace channel vector,
and U ∈ C
N
t
×N
t
is the beamformin g matrix expressed as
U =
b
H
(Ω
1
), b
H
(Ω
2
),...,b
H
(Ω
N
t
)
. (7)
TheAoDvalueset{Ω
1
, Ω
2
,...,Ω
N
t
} contains N
t
different
spatial directions; therefore, b (Ω
1
),...,b (Ω
N
t
) comprise a
set of basic 3-D beams. According to (6) and (7), the beamspace
channel vector
˜
h
i
is another linear p resentation of h
i
and
reflects the channel energy distribution on the basic b eams. In
addition, different choices of U contribute to different trans-
formation results. Next, we introduce two kinds of beamspace
transformations, namely, broadcasting beamforming and dedi-
cated beamforming.
A. Broadcasting Beamforming
As the n ame suggests, broadcasting beamforming is a
beamspace transformation method ap plicable to all users’ spa-
tial channel vectors under the same system deployment, re-
gardless of each user’s AoD/angle o f arrival (AoA). It chooses
N
t
beams corresponding to N
t
uniformly distributed spatial
directions to be the set of basic beams. The jth basic b eam used
in the broadcasting beamforming matrix is
b
DFT
(Ω
j
)=a
(v)
t
m
N
(v)
t
⊗ a
(h)
t
n
N
(h)
t
(8)
where j =mN
(h)
t
+n, m=0,...,N
(v)
t
−1,n=0,...,N
(h)
t
−
1. These discrete Fourier transforming (DFT)-based beams
are orthogonal to each other and covers N
t
fixed directions
independent with any user channel, as shown in Fig. 2. If we
denote
V
(v)
DFT
=
a
(v)
t
(0), a
(v)
t
1
N
(v)
t
,...,a
(v)
t
N
(v)
t
− 1
N
(v)
t
V
(h)
DFT
=
a
(h)
t
(0), a
(h)
t
1
N
(h)
t
,...,a
(h)
t
N
(h)
t
− 1
N
(h)
t
(9)