逆波兰表达式解析与实现

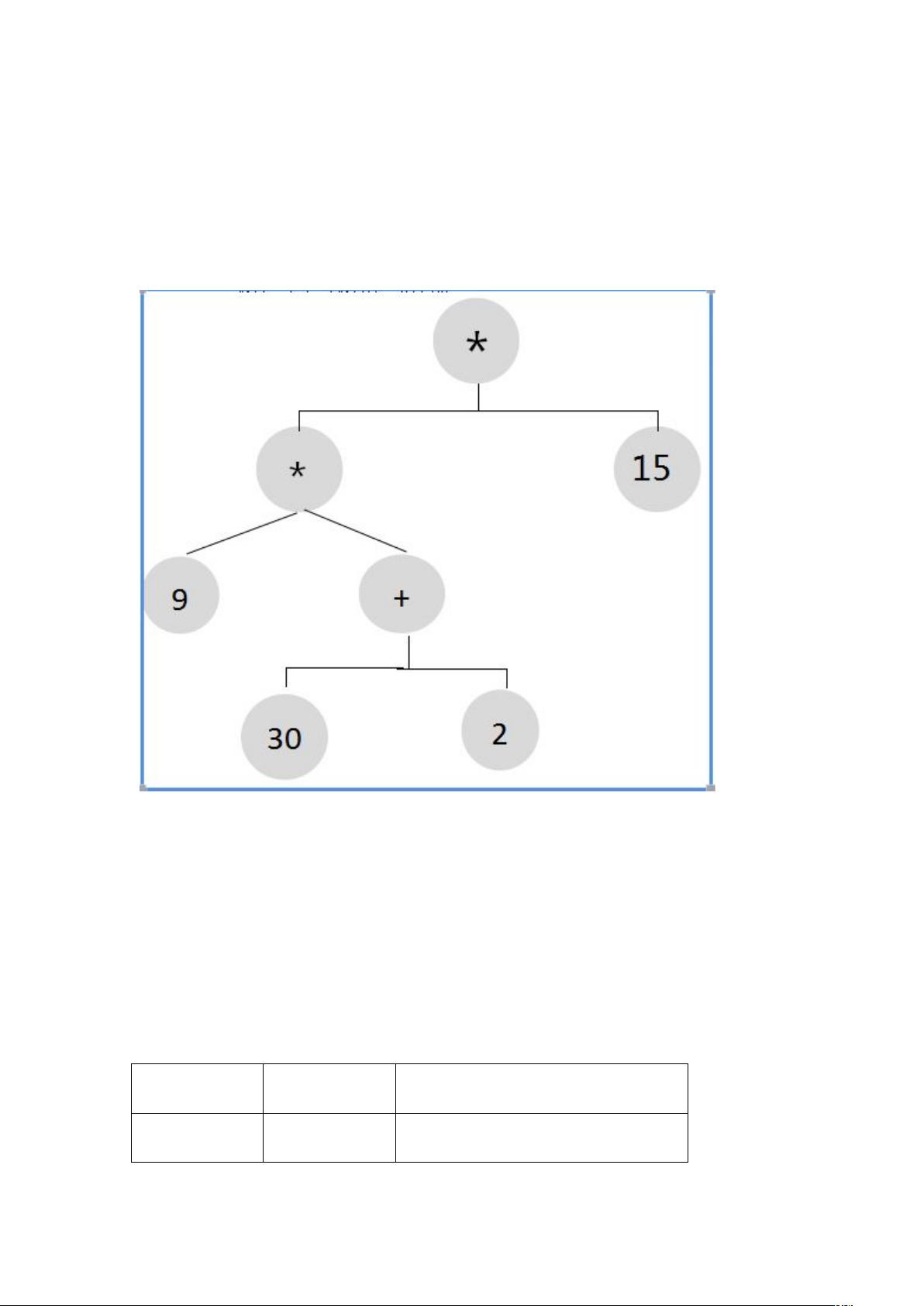
"逆波兰表达式实现" 逆波兰表达式，又称后缀表达式，是一种特殊的数学表达式表示方法，它的特点在于运算符位于其操作数之后。这种表示方式常用于算法设计，特别是在解析和计算数学表达式时，因为它的计算过程与二叉树的后序遍历非常吻合。在逆波兰表达式中，每个运算符紧跟在其操作数后面，这使得计算表达式的过程变得简单，只需要一个栈即可完成。 例如，常规的中缀表达式"9 * (30 + 2) * 15"在逆波兰表达式中写作"9 30 2 + * 15 *"。这里的计算顺序遵循先乘除后加减，先括号内的运算的原则。在后缀表达式中，"9 30 2 +"这部分首先计算，得到"32"，然后"32 * 15"得到最终结果"480"。 将中缀表达式转换为后缀表达式通常涉及以下步骤： 1. 遍历输入的中缀表达式。 2. 遇到数字时，将其压入栈中。 3. 遇到运算符时，与栈顶的运算符比较优先级。如果当前运算符优先级更高或栈为空，将当前运算符压入栈；否则，弹出栈顶运算符并将其与当前运算符组合成一个新的后缀表达式，直到当前运算符的优先级高于栈顶运算符。 4. 遇到左括号"("，将其压入栈中。 5. 遇到右括号")"，连续弹出栈中的运算符，直到遇到左括号，将这些运算符组合成一个新的后缀表达式，并丢弃左括号。 6. 最终，栈中剩余的运算符依次组合成后缀表达式。 在实现逆波兰表达式的计算时，通常使用一个栈来存储运算符。按照后缀表达式从左到右读取每个元素，如果是数字则直接入结果栈，如果是运算符则取出栈顶的操作数进行运算，并将结果压回栈中。这个过程持续到所有元素处理完毕，栈顶的元素就是表达式的结果。 在编程实现时，需要注意以下几个关键点： - 输入的字符串可能包含未知长度和内容，需要设计适当的数据结构（如队列）来存储。 - 运算符有优先级，需要建立一个映射表来确定运算符的优先级。 - 在转换过程中，需要正确处理括号，确保它们对应的操作数被正确处理。 - 在计算过程中，确保运算符的结合性和操作数的类型匹配，遵循正确的运算规则。 策略1 提供了一种检查输入合法性的方式，确保输入的表达式可以被正确解析。 策略2 描述了如何根据后缀表达式计算结果，通过构建虚拟的二叉树结构，模拟运算过程。 逆波兰表达式是一种有效的表达式表示和计算方法，尤其适用于算法实现。理解和掌握其转换和计算原理对于学习数据结构和算法至关重要。