神经网络编程基础：从逻辑回归到梯度下降

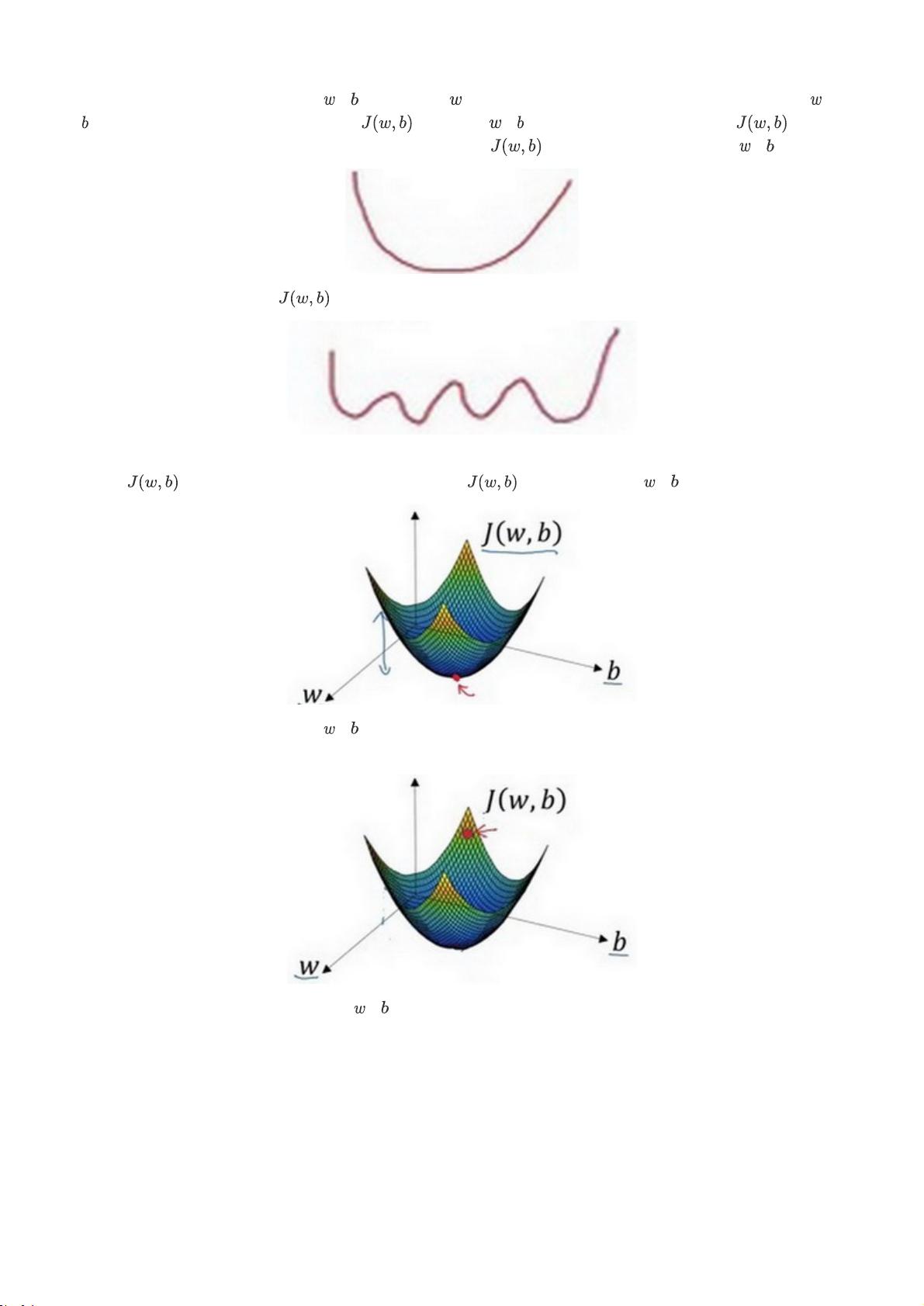
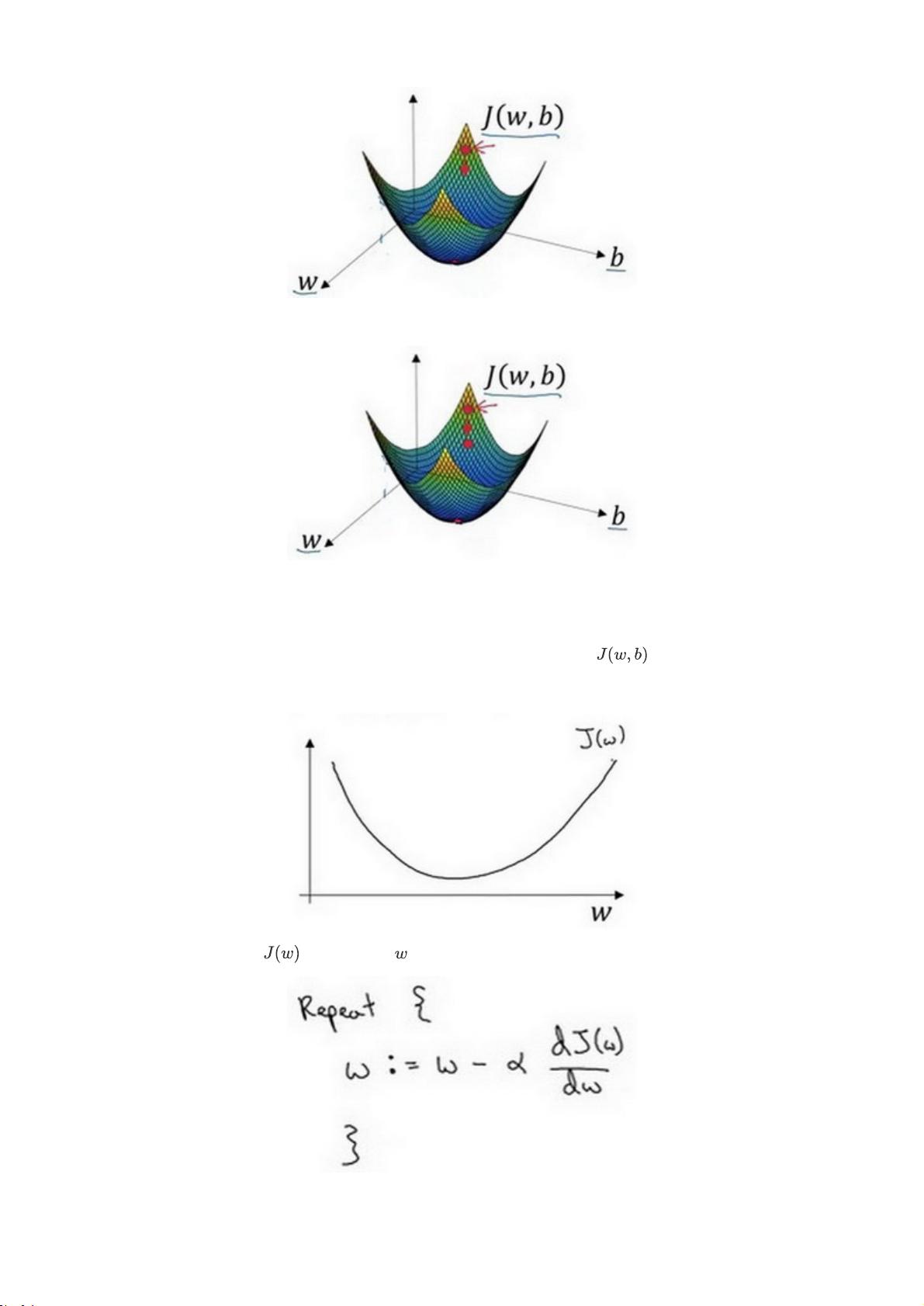
本周的课程深入探讨了神经网络编程的基础，主要内容涵盖了以下几个关键知识点： 1. **二分类（Binary Classification）**：作为神经网络的入门，理解如何将问题分为两个类别是基础。在二分类任务中，目标是通过学习算法将数据点划分到预定义的两类中。 2. **逻辑回归（Logistic Regression）**：作为最简单的神经网络模型，逻辑回归用于解决分类问题。它使用sigmoid函数来预测概率，并通过最大化似然函数或最小化对数损失函数来进行训练。 3. **逻辑回归的代价函数（Logistic Regression Cost Function）**：这个函数衡量模型预测结果与实际标签之间的差异，常用交叉熵损失函数，是优化过程的核心。 4. **梯度下降法（Gradient Descent）**：一种优化算法，通过迭代更新模型参数以最小化代价函数，是训练神经网络的基本优化技术。 5. **导数（Derivatives）**：在神经网络中，导数是理解代价函数如何随参数变化的关键，它帮助我们确定参数更新的方向。 6. **计算图（Computation Graph）**：可视化模型结构和计算流程的方法，有助于理解和优化计算效率。 7. **使用计算图求导数（Derivatives with a Computation Graph）**：利用图形模型来自动计算梯度，简化了导数的计算过程。 8. **逻辑回归中的梯度下降（Logistic Regression Gradient Descent）**：具体应用梯度下降方法优化逻辑回归模型的过程。 9. **m个样本的梯度下降（Gradient Descent on m Examples）**：扩展到多例数据时，梯度下降的处理策略。 10. **向量化（Vectorization）**：提高代码效率的技术，通过数组运算代替循环，加速了大规模数据处理。 11. **Python中的广播（Broadcasting in Python）**：在向量化操作中，Python NumPy库的广播机制使得向量和标量运算更为便捷。 12. **向量化的更多例子（More Examples of Vectorization）**：展示了向量化技术在不同场景的应用实例。 13. **向量化逻辑回归（Vectorizing Logistic Regression）**：将逻辑回归模型转化为向量化形式，提升计算性能。 14. **向量化logistic回归的梯度输出（Vectorizing Logistic Regression's Gradient）**：计算向量化逻辑回归的梯度，是向量化的重要组成部分。 15. **Python NumPy向量的说明（An Note on Python or NumPy Vectors）**：关于Python科学计算库NumPy中向量操作的详细说明。 16. **Jupyter/iPython Notebooks快速入门（Quick Tour of Jupyter/iPython Notebooks）**：介绍数据科学家常用的交互式编程环境，方便实验和记录。 17. **可选阅读：logistic损失函数的解释（Optional Reading: Explanation of Logistic Regression Cost Function）**：提供深入理解代价函数背后原理的机会。 这一周的课程内容着重于理论与实践相结合，从基础概念到实际操作，让学生逐步掌握神经网络编程的基石，包括如何构建、优化和利用逻辑回归进行分类任务。同时，通过Python编程和工具如Jupyter Notebook的使用，增强了学习者对神经网络开发的理解和实践能力。