概率统计三大分布:卡方、t与F分布解析
需积分: 48 44 浏览量
更新于2024-07-09
2
收藏 1.27MB PDF 举报
"该资源是关于概率统计中三个重要分布的总结——卡方分布、t分布和F分布的介绍。内容涵盖了这些分布的起源、特点以及如何理解和应用。"
在统计学和概率论中,卡方分布(χ²分布)、t分布和F分布是常用的连续概率分布,尤其在假设检验和置信区间估计中扮演着关键角色。
1. **卡方分布 (χ² distribution)**:
- 卡方分布是由多个独立同分布的标准正态随机变量平方后的和构成的分布,它通常用于检验观测值与理论值之间的差异是否显著,如在卡方拟合优度检验和卡方独立性检验中。
- 自由度决定了卡方分布的具体形状,随着自由度的增加,卡方分布逐渐接近正态分布。
2. **t分布**:
- t分布是由一个正态分布的随机变量除以其标准差的t倍,其中t是独立的卡方分布随机变量(自由度为n-1)的平方根,n是样本大小。
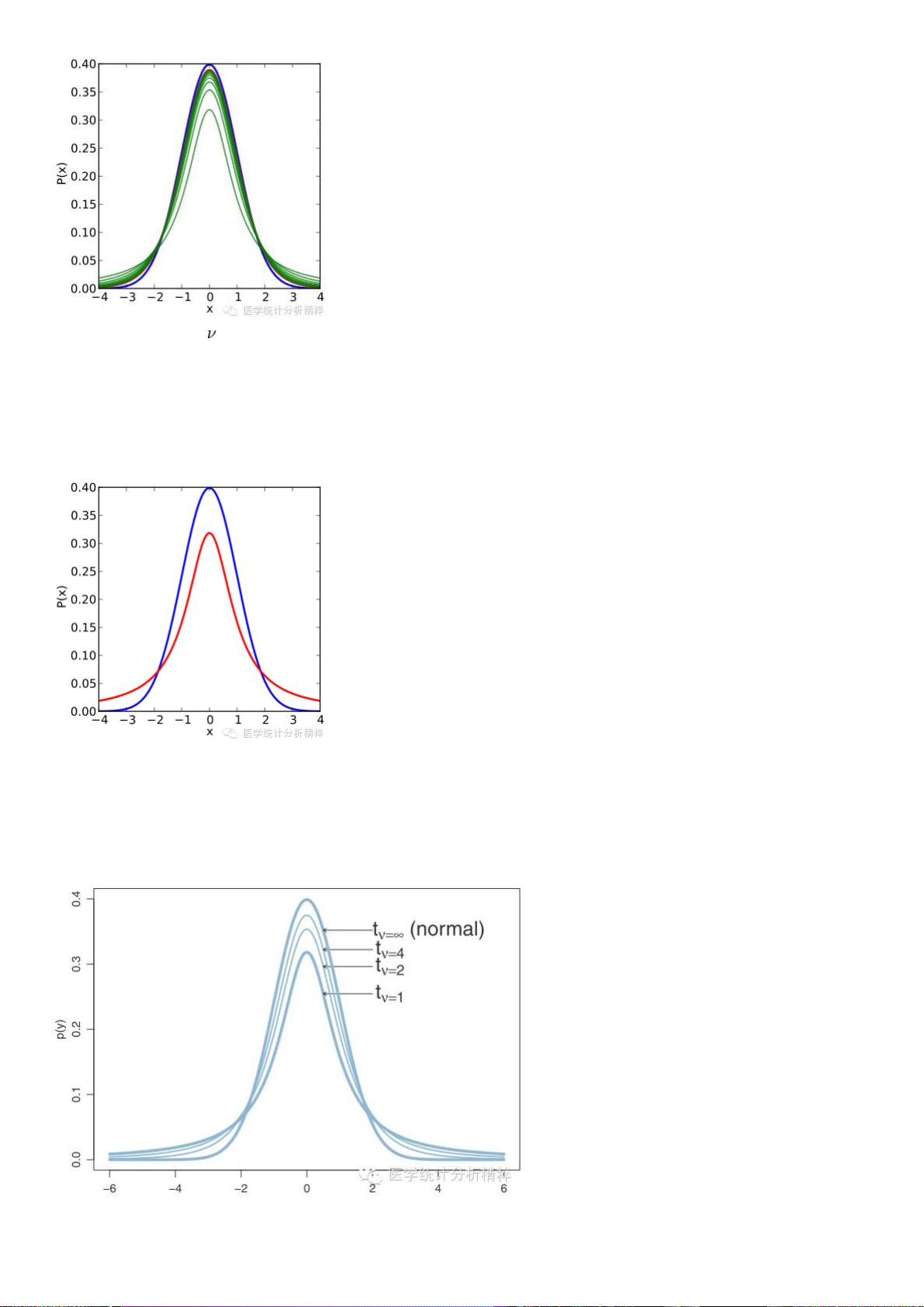
- t分布由它的自由度定义,自由度越小,分布的尾部越重,即分布更偏离正态分布,对异常值更敏感。
- 在小样本情况下,t分布常用于估计总体均值,如t检验,因为它对样本量小的不确定性进行了调整。
- 随着样本量增大,t分布逐渐逼近正态分布。因此,当样本量足够大(例如超过30或50)时,t分布可以用正态分布近似。
3. **F分布**:
- F分布是两个独立卡方分布的比例,通常出现在两个独立估计的方差比率的比较中,如方差分析(ANOVA)和方差齐性检验。
- F分布有两个自由度参数,分别对应两个卡方分布的自由度。
- 其形状取决于这两个自由度,随着其中一个自由度的增大,F分布的峰值降低,而尾部变薄。
理解这些分布的关键在于它们与样本大小的关系以及在假设检验中的应用。t分布的出现解决了小样本情况下对总体参数估计的问题,而F分布则用于比较不同组间的方差。卡方分布则在检验模型拟合程度和独立性时发挥重要作用。在实际应用中,掌握这些分布的特性,能帮助我们选择合适的统计方法,有效地分析数据并做出科学的推断。
2021-05-31 上传
2010-08-09 上传
2018-11-06 上传
2024-10-19 上传
2020-05-08 上传
2021-07-03 上传
2021-09-17 上传
2022-04-29 上传
2022-04-29 上传
wozijisunfly
- 粉丝: 11
- 资源: 42
最新资源
- Angular程序高效加载与展示海量Excel数据技巧
- Argos客户端开发流程及Vue配置指南
- 基于源码的PHP Webshell审查工具介绍
- Mina任务部署Rpush教程与实践指南
- 密歇根大学主题新标签页壁纸与多功能扩展
- Golang编程入门:基础代码学习教程
- Aplysia吸引子分析MATLAB代码套件解读
- 程序性竞争问题解决实践指南
- lyra: Rust语言实现的特征提取POC功能
- Chrome扩展:NBA全明星新标签壁纸
- 探索通用Lisp用户空间文件系统clufs_0.7
- dheap: Haxe实现的高效D-ary堆算法
- 利用BladeRF实现简易VNA频率响应分析工具
- 深度解析Amazon SQS在C#中的应用实践
- 正义联盟计划管理系统:udemy-heroes-demo-09
- JavaScript语法jsonpointer替代实现介绍