2329-9290 (c) 2018 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission. See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
This article has been accepted for publication in a future issue of this journal, but has not been fully edited. Content may change prior to final publication. Citation information: DOI 10.1109/TASLP.2018.2842159, IEEE/ACM
Transactions on Audio, Speech, and Language Processing
IEEE/ACM TRANSACTIONS ON AUDIO, SPEECH, AND LANGUAGE PROCESSING, VOL. X, NO. X, XXX XXXX
in Fig. 2(c).
D. Spectral Magnitude Mask
The spectral magnitude mask (SMM) (called FFT-MASK
in [178]) is defined on the STFT (short-time Fourier
transform) magnitudes of clean speech and noisy speech:
where
and
represent spectral magnitudes of
clean speech and noisy speech, respectively. Unlike the IRM,
the SMM is not upper-bounded by 1. To obtain separated
speech, we apply the SMM or its estimate to the spectral
magnitudes of noisy speech, and resynthesize separated
speech with the phases of noisy speech (or an estimate of
clean speech phases). Fig. 2(e) illustrates the SMM.
E. Phase-Sensitive Mask
The phase-sensitive mask (PSM) extends the SMM by
including a measure of phase [41]:
where denotes the difference of the clean speech phase and
the noisy speech phase with the T-F unit. The inclusion of the
phase difference in the PSM leads to a higher SNR, and tends
to yield a better estimate of clean speech than the SMM [41].
An example of the PSM is shown in Fig. 2(f).
F. Complex Ideal Ratio Mask
The complex ideal ratio mask (cIRM) is an ideal mask in
the complex domain. Unlike the aforementioned masks, it can
perfectly reconstruct clean speech from noisy speech [188]:
where , denote the STFT of clean speech and noisy speech,
respectively, and ‘ ’ represents complex multiplication.
Solving for mask components results in the following
definition:
where
and
denote real and imaginary components of
noisy speech, respectively, and
and
real and imaginary
components of clean speech, respectively. The imaginary unit
is denoted by ‘i’. Thus the cIRM has a real component and an
imaginary component, which can be separately estimated in
the real domain. Because of complex-domain calculations,
mask values become unbounded. So some form of
compression should be used to bound mask values, such as a
tangent hyperbolic or sigmoidal function [188] [184] .
Williamson et al. [188] observe that, in Cartesian
coordinates, structure exists in both real and imaginary
components of the cIRM, whereas in polar coordinates,
structure exists in the magnitude spectrogram but not phase
spectrogram. Without clear structure, direct phase estimation
would be intractable through supervised learning, although we
should mention a recent paper that uses complex-domain
DNN to estimate complex STFT coefficients [107]. On the
other hand, an estimate of the cIRM provides a phase estimate,
a property not possessed by PSM estimation.
G. Target Magnitude Spectrum
The target magnitude spectrum (TMS) of clean speech, or
, is a mapping-based training target [116] [196] [57]
[197]. In this case supervised learning aims to estimate the
magnitude spectrogram of clean speech from that of noisy
speech. Power spectrum, or other forms of spectra such as mel
spectrum, may be used instead of magnitude spectrum, and a
log operation is usually applied to compress the dynamic
range and facilitate training. A prominent form of the TMS is
the log-power spectrum normalized to zero mean and unit
variance [197]. An estimated speech magnitude is then
combined with noisy phase to produce the separated speech
waveform. In terms of cost function, MSE is usually used for
TMS estimation. Alternatively, maximum likelihood can be
employed to train a TMS estimator that explicitly models
output correlation [175]. Fig. 2(g) shows an example of the
TMS.
H. Gammatone Frequency Target Power Spectrum
Another closely related mapping-based target is the
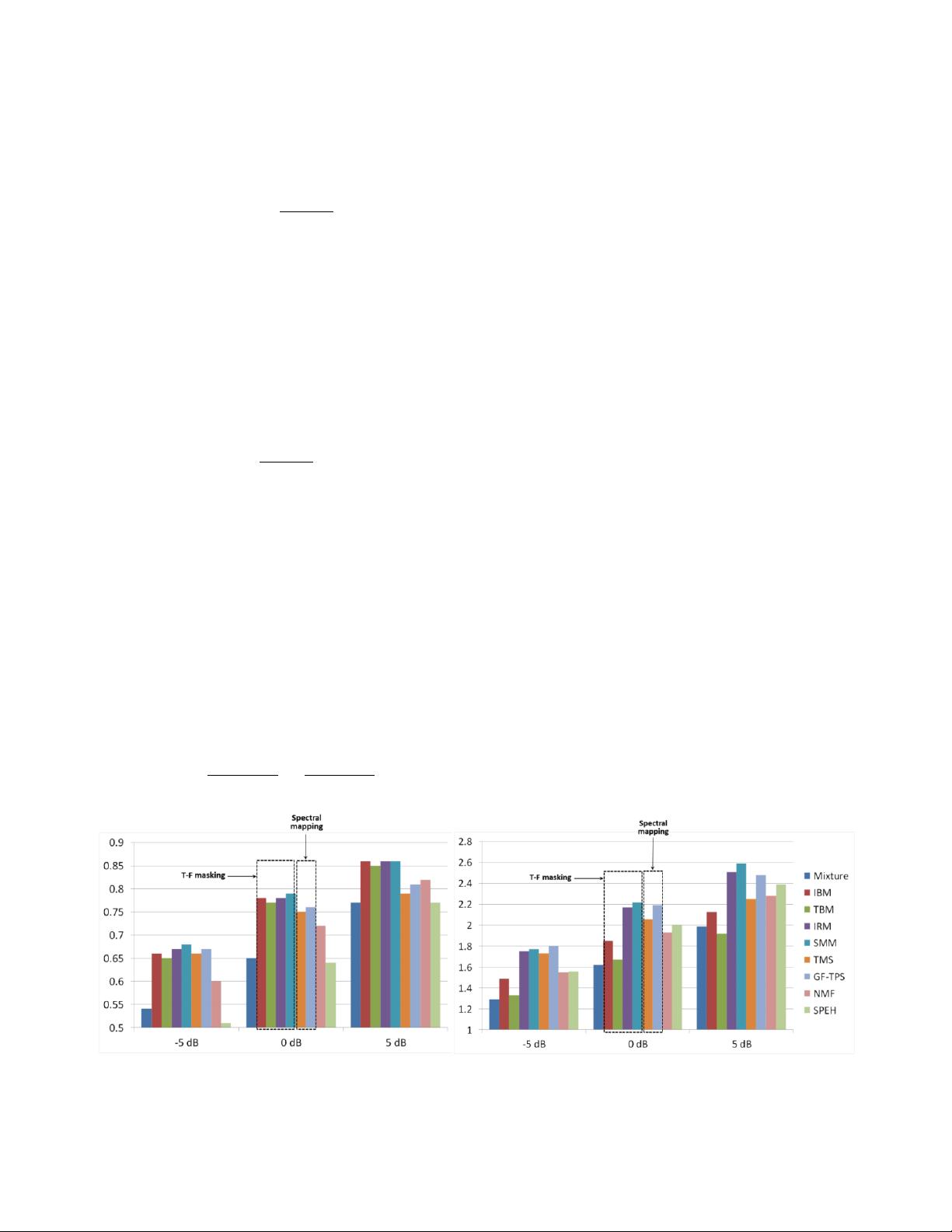
(a) STOI results (b) PESQ results
Figure 3. Comparison of training targets. (a) In terms of STOI. (b) In terms of PESQ. Clean speech is mixed with a factory noise at
-5 dB, 0 dB and 5 dB SNR. Results for different training targets as well as a speech enhancement (SPEH) algorithm and an NMF
method are highlighted for 0 dB mixtures. Note that the results and the data in this figure can be obtained from a Matlab toolbox at
http://web.cse.ohio-state.edu/pnl/DNN_toolbox/.









