堆数据结构详解：完全二叉树实现与API设计

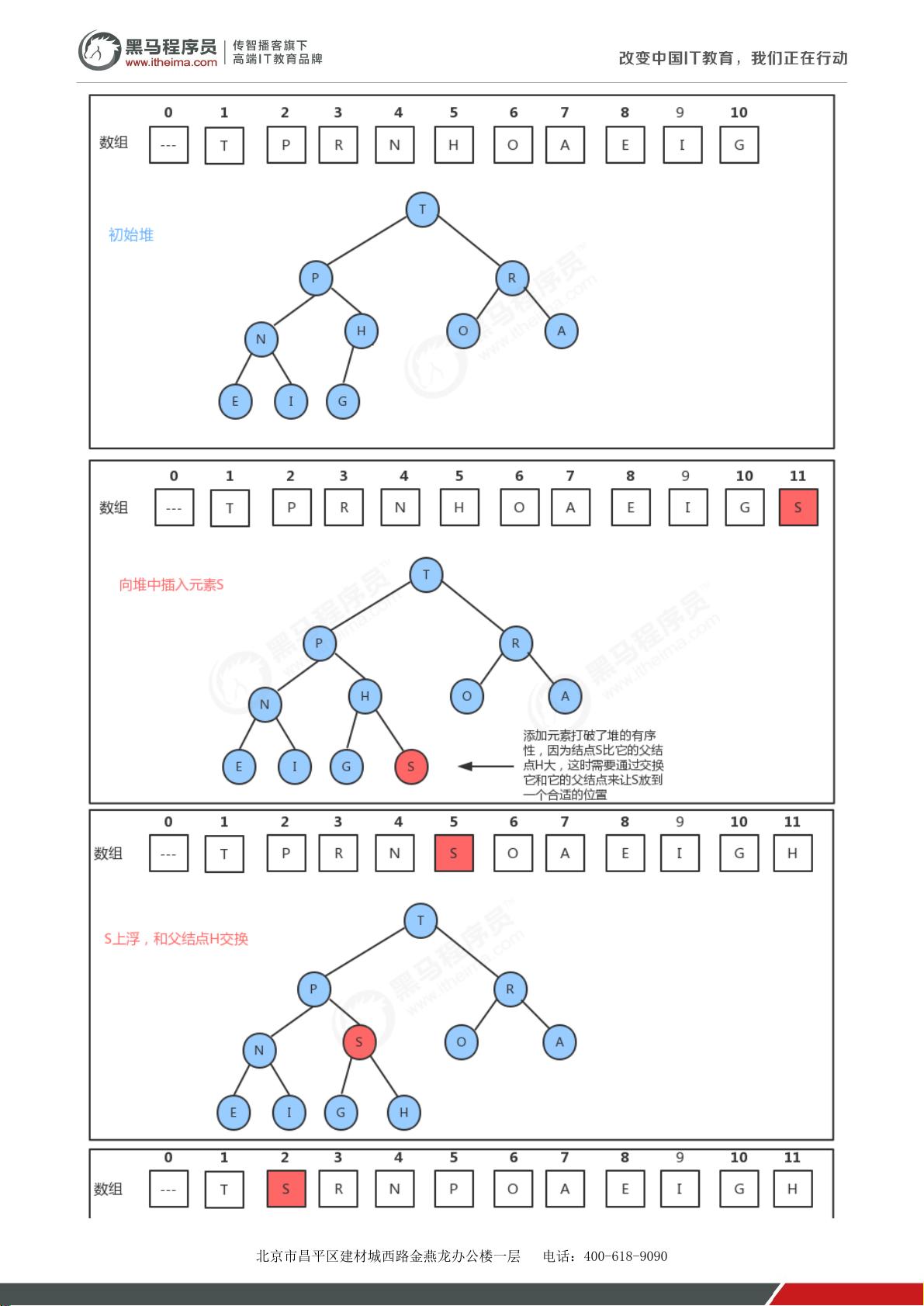
堆是一种特殊的树形数据结构，通常在计算机科学中用于优先队列的实现，特别是在需要快速访问最大（或最小）元素的场景下。堆可以看作是一棵完全二叉树，具有以下特点： 1. 完全性：除了最底层，堆的每一层都是满的，且从左到右填充。如果最底层不满，必须遵循“左满右不满”的规则。 2. 数组表示：堆常使用数组来物理上存储，通过索引映射到二叉树的节点关系。根节点通常位于数组的第1个位置，后续节点的索引按照层次递增，如子节点的索引为父节点索引的两倍加1。 3. 堆的特性： - 每个节点的值大于或等于其子节点的值，但并不一定大于右侧子节点，这与二叉搜索树的性质不同。 - 插入和删除操作都有特定的算法支持，例如`insert()`方法用于添加新元素，`delMax()`方法用于删除并返回堆顶的最大元素。 4. 常见操作： - `less(int i, int j)`：比较索引i和j处元素的大小。 - `exch(int i, int j)`：交换堆中索引i和j处的元素值。 - `swim(int k)`：上浮操作，确保索引k处元素满足堆的性质。 - `sink(int k)`：下沉操作，确保在插入或调整后，堆的结构仍然保持。 5. 成员变量： - `T[] items`：存储元素的数组。 - `int N`：记录堆中元素的数量。 - 计算索引：堆中的节点索引与其在树中的位置之间可以通过简单的数学运算关联，无需使用指针。 堆的API设计通常围绕这些核心操作展开，提供一组高效的方法来维护堆的特性。在实现过程中，需要注意插入和删除操作的性能优化，比如插入时的上浮调整，以及删除最大元素后的下沉调整。 堆的实现涉及数组操作，特别是当需要频繁访问或修改堆顶元素时，堆的优势尤为明显。此外，堆还有多种类型，包括最大堆（父节点总是大于子节点）和最小堆（父节点总是小于子节点），选择哪种类型取决于具体的应用需求。堆是一种基础但实用的数据结构，对于排序、优先级队列等场景有着广泛的应用。