遗传算法求解TSP问题：优化路径并追踪最短路线

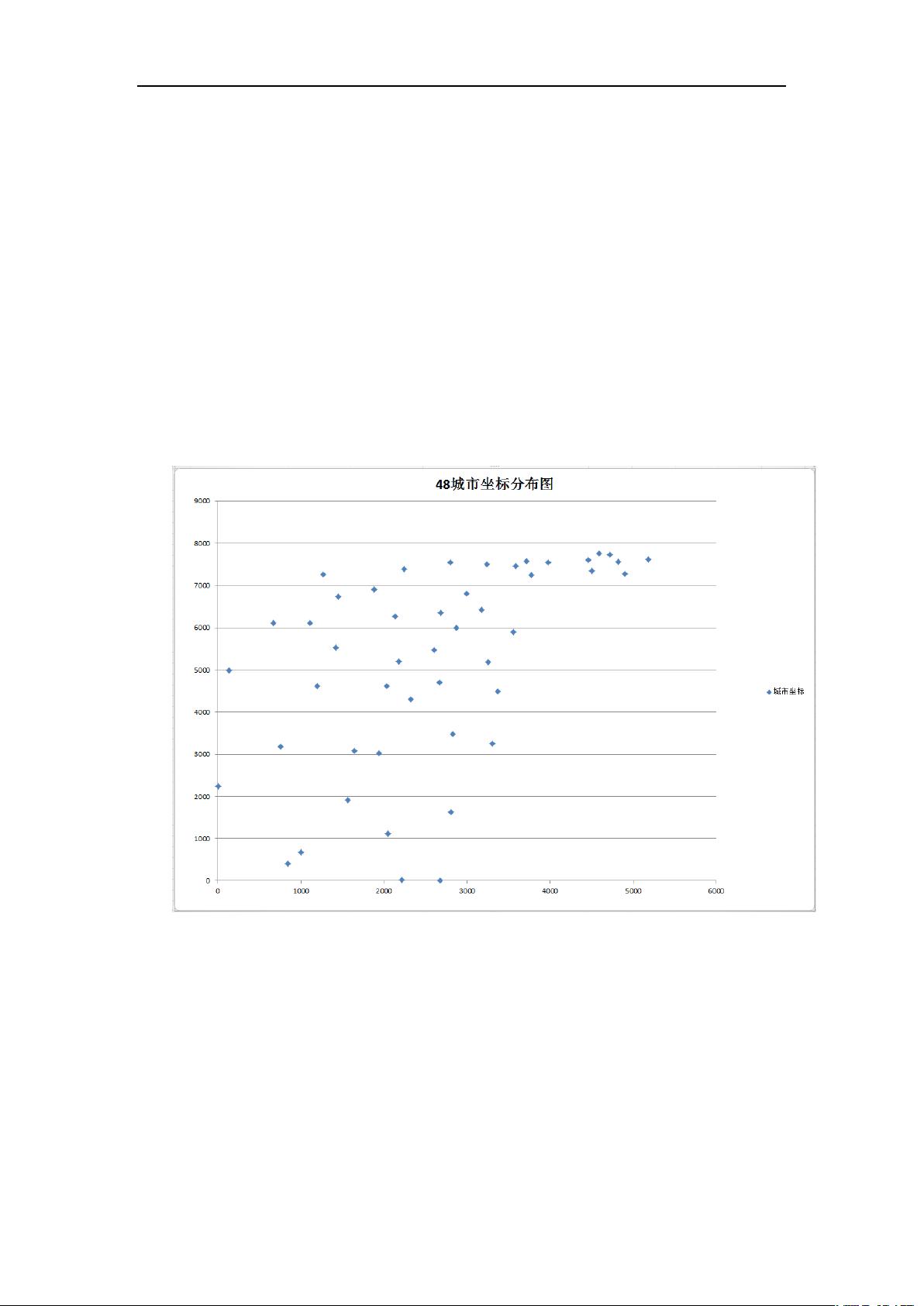
遗传算法在解决旅行商问题（Traveling Salesman Problem, TSP）中展现出强大的潜力，尤其是在处理大规模问题时。本篇文章主要围绕TSP问题的实验环境、问题背景、传统方法的局限以及遗传算法的应用展开讨论。 首先，实验环境设置了在一台Intel i5-2450M处理器上运行，内存为6GB，操作系统为Windows 7 64位，使用Java作为实现语言。具体案例采用的是TSPLIB库中的att48数据集，这是一个包含48个城市的数据集，具有最优路径长度10628，适合进行遗传算法的实践。 旅行商问题是一个经典的组合优化问题，目标是寻找一条经过所有城市的路径，使得总行程最短，但每个城市仅能访问一次且最后返回起点。传统方法如穷举法和动态规划在城市数量增加时效率极低，而贪婪算法在某些情况下可能无法找到全局最优解。因此，遗传算法因其能够处理大规模问题并寻求全局最优特性，成为解决TSP问题的一个有效工具。 遗传算法的核心步骤包括： 1. 初始化阶段：设置种群规模、城市数量、运行代数等参数，将城市坐标转化为距离矩阵，并随机生成初始种群，即多个路径序列。 2. 计算种群适应度：对于每条路径，通过求和其各段距离来评估其适应度，即路径的总长度。 3. 计算累计概率：根据适应度值，计算每个个体在整个种群中的累积概率，这用于选择算子和评价个体在进化过程中的重要性。 4. 迭代过程：采用赌轮选择策略来挑选下一代个体，通过交叉和变异操作进行基因重组，交叉通常发生在特定的概率节点，变异则随机改变部分基因。每次迭代后，更新种群适应度和个体概率，并记录最优解。 5. 输出阶段：在迭代过程中，输出最短路径长度以及对应的最短路径，这通常是整个算法执行的最终目标。 通过遗传算法的迭代优化，可以期望在有限的计算资源下找到接近或达到全局最优的TSP解决方案。这种基于生物进化原理的优化方法为解决复杂问题提供了有效的途径。