深入理解二叉树：概念、术语与遍历

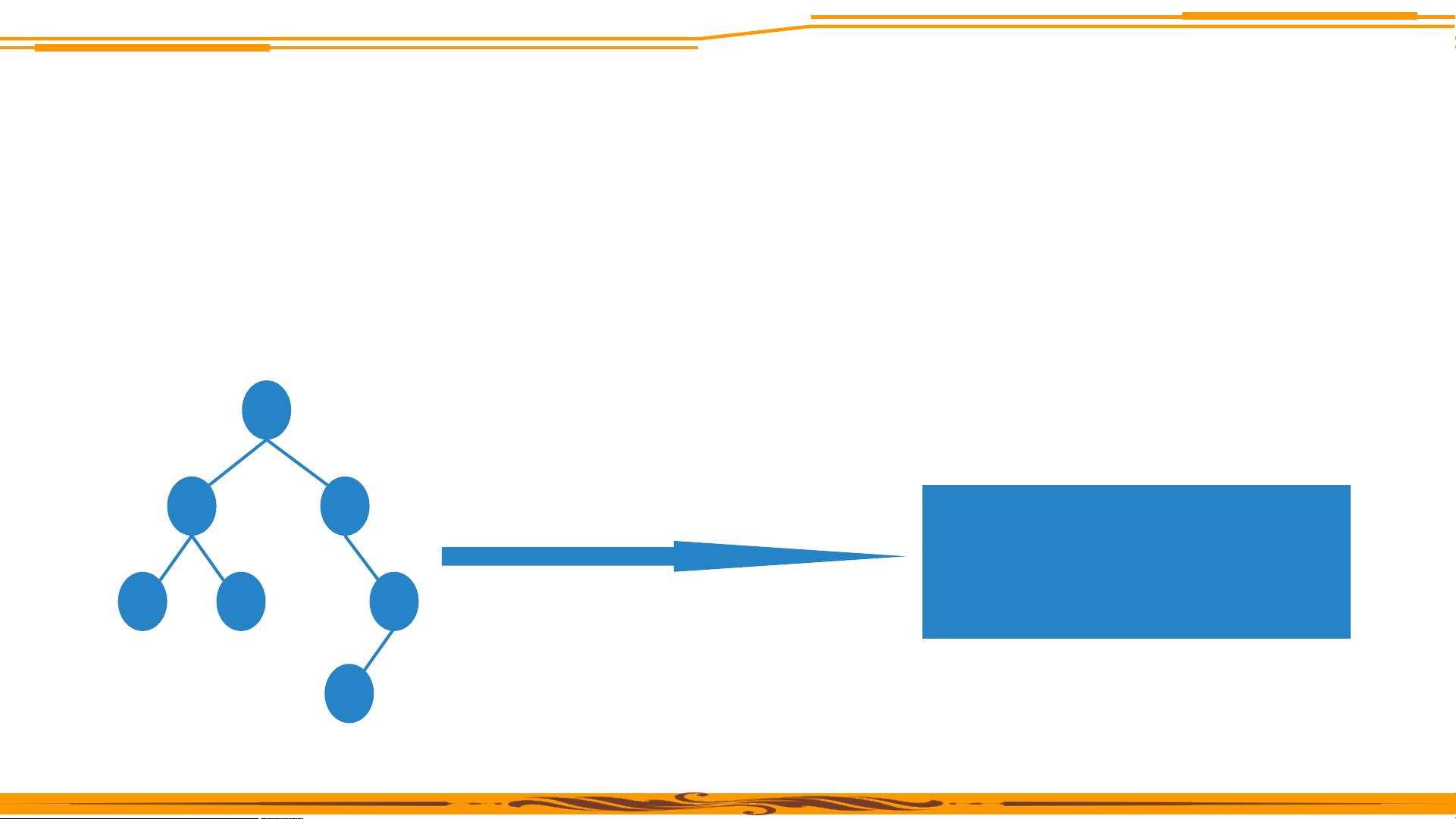
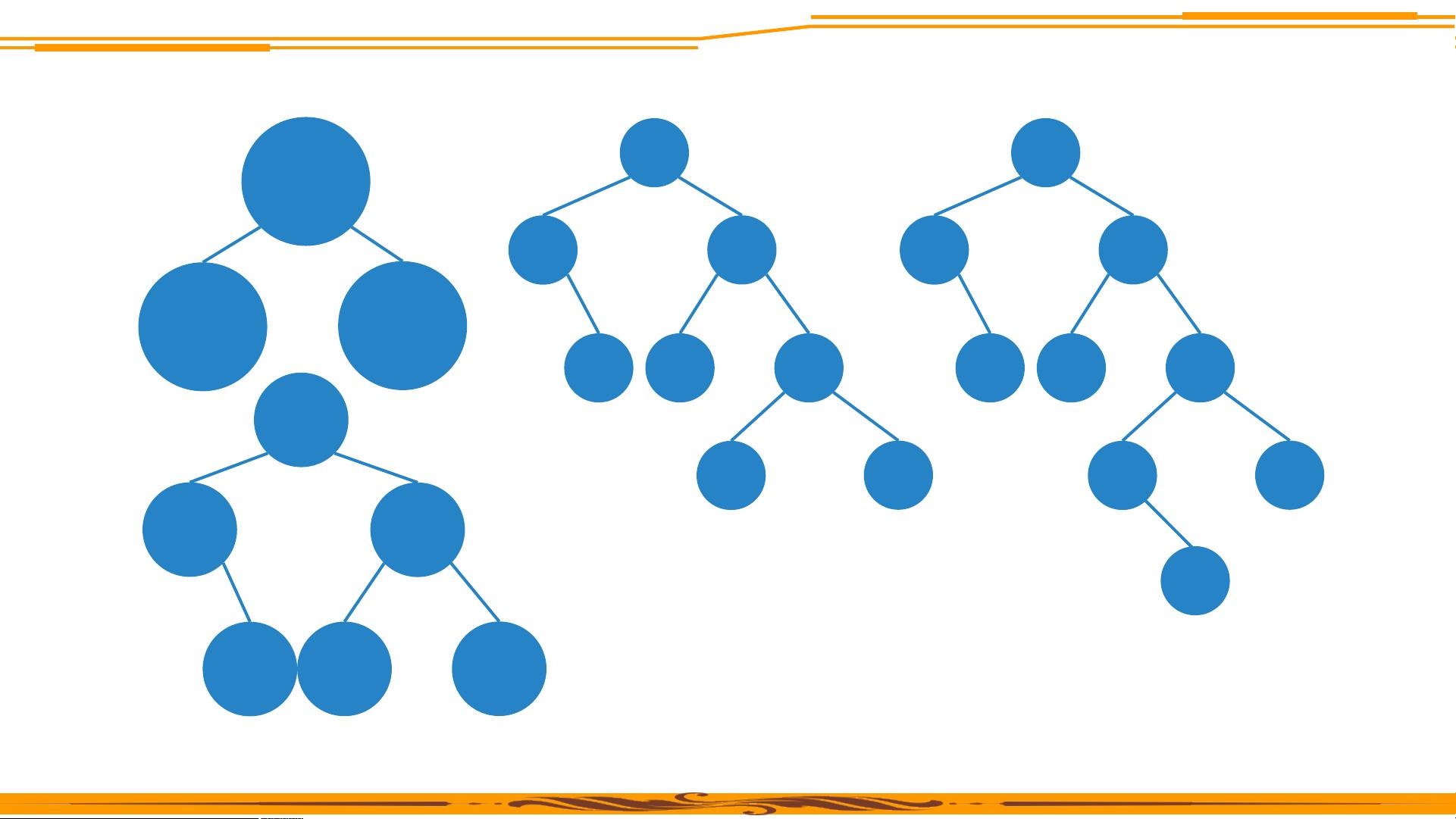
第四章的主题深入探讨了二叉树及其在算法与数据结构课程中的重要性。二叉树是一种基本的数据结构，它由一个根节点和两个互不相交的子树组成，每个节点最多有两个子节点，形成一种层次关系。本章主要关注以下几个关键知识点： 1. 二叉树的基本概念： - 定义：二叉树是结点的集合，非空时包含一个根节点和两个不相交的子树（左子树和右子树），且不存在环路。 - 基本术语：包括父节点、子节点、兄弟节点、叶子节点，树边（连接节点的边）、路径、节点度（子节点数量）、二叉树的深度（从根到最远叶子节点的边的数量）。 2. 特殊的二叉树类型： - 满二叉树：所有节点都有两个子节点，除了最底层的叶子节点。 - 完全二叉树：除最后一层外，所有层都是满的，且最后一层左侧已满，右侧尽可能多的填入节点。 - 扩充二叉树：通过添加空节点，使非满二叉树变为满二叉树，便于处理。 3. 二叉树的性质： - 非空二叉树的层数和节点数量关系：性质1提到不同层的最大节点数。 - 具体结点位置关系：如完全二叉树的节点编号规则，以及满二叉树和扩充二叉树的特殊计数规律。 - 遍历方式：介绍先序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）的顺序。 这些知识点在实际编程中至关重要，尤其是在处理树形数据结构的问题时，如文件系统、表达式解析、图的遍历等。理解二叉树的特性有助于优化搜索、排序和存储效率，是数据结构和算法设计的基础。通过掌握这些内容，学生能够更好地设计和实现高效的算法，并在解决复杂问题时做出明智的选择。在后续的学习中，可能会涉及二叉树的插入、删除和查找操作，以及它们在各种数据结构（如堆、平衡二叉搜索树）中的应用。