Dijkstra算法实现与流程解析

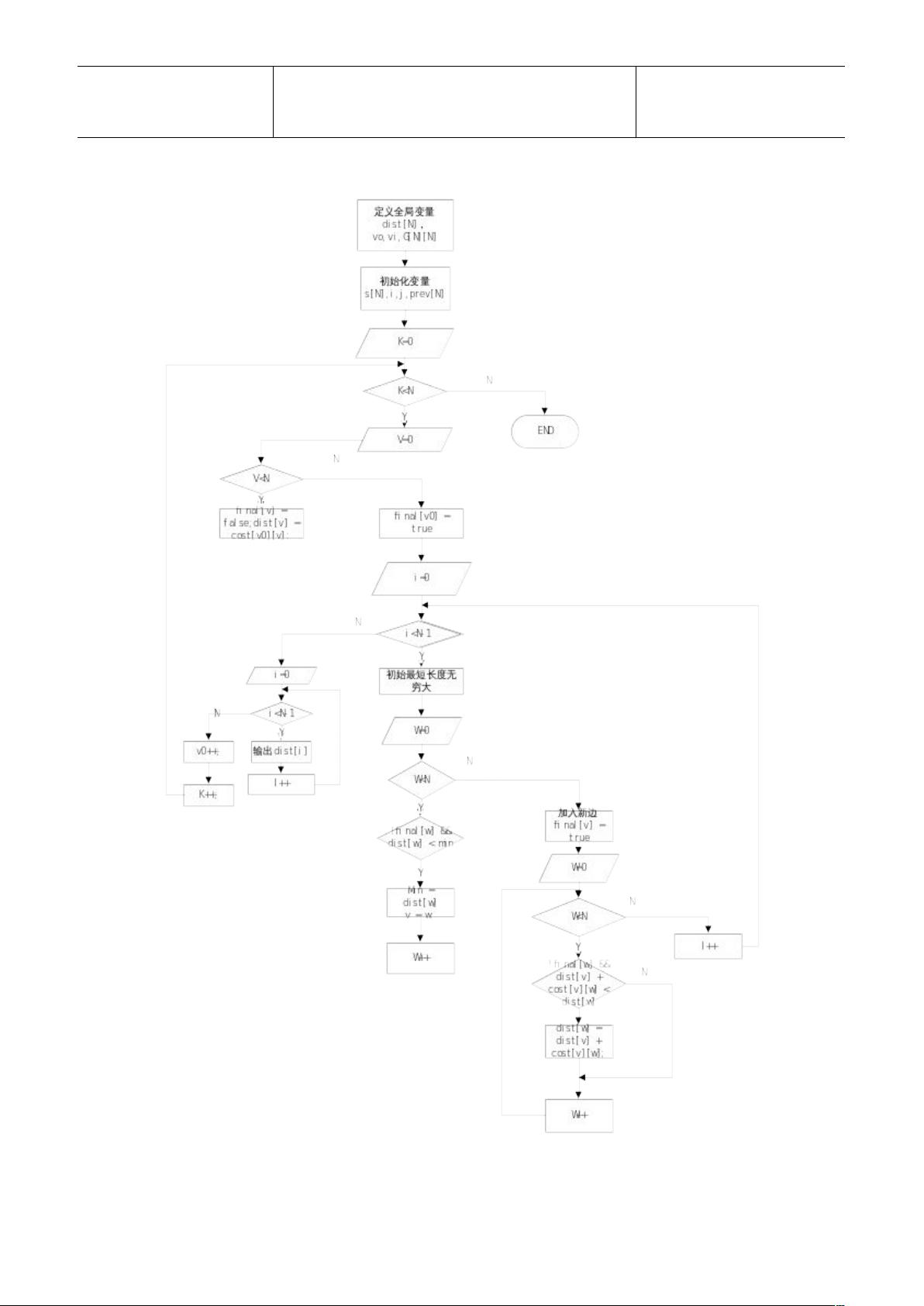
"Dijkstra算法的流程图及其应用的说明文档" Dijkstra算法是一种经典的图论算法，主要用于寻找图中单源最短路径。这个算法由荷兰计算机科学家艾兹格·迪科斯彻提出，适用于带有非负权重的图。在这个流程图中，详细展示了Dijkstra算法的执行步骤。 Dijkstra算法的主要思路是从一个指定的起点（源点）开始，逐步扩展到其他节点，每次扩展都是找到当前未访问节点中距离源点最近的一个，更新其邻居节点的距离。这个过程不断重复，直到所有节点都被访问过。算法的核心在于维护一个优先队列（通常是基于最小堆实现），用于存储未访问节点并根据距离排序，保证每次选择的是距离最小的节点。 以下是Dijkstra算法的详细步骤： 1. 初始化：设定源点的距离为0，其他所有节点的距离为无穷大。创建一个未访问节点集合，并将所有节点加入。 2. 循环直到未访问节点集合为空： - 从未访问节点集合中取出距离源点最近的节点u（使用优先队列实现）。 - 将节点u标记为已访问。 - 遍历u的所有邻居v： - 如果通过u到达v的距离小于当前记录的v到源点的距离，更新v的距离为dist[u] + w[u, v]，其中w[u, v]表示u到v的边的权重。 3. 结束：当所有节点都标记为已访问时，dist数组中的每个元素代表了对应节点到源点的最短路径长度。 在提供的程序源代码中，采用了邻接矩阵来存储图的结构。邻接矩阵是一个二维数组，其中的元素w[u, v]表示顶点u到顶点v的边的权重。程序允许用户输入图的边权重，然后计算并输出任意两个顶点之间的最短路径。 用户手册简单明了，强调用户需要初始化二维数组以存储边的权重，程序会自动处理Dijkstra算法的计算和输出。设计思想体现了Dijkstra算法的基本逻辑，即每次迭代选择最近未访问节点并更新其邻居的距离。 Dijkstra算法是一个高效解决单源最短路径问题的工具，尤其适用于非负权重的图。在实际应用中，如路由选择、网络调度等领域都有广泛的应用。这个流程图和相关的程序实现提供了直观的理解和实践基础。