C语言实现数值分析算法：gauss消去与迭代法

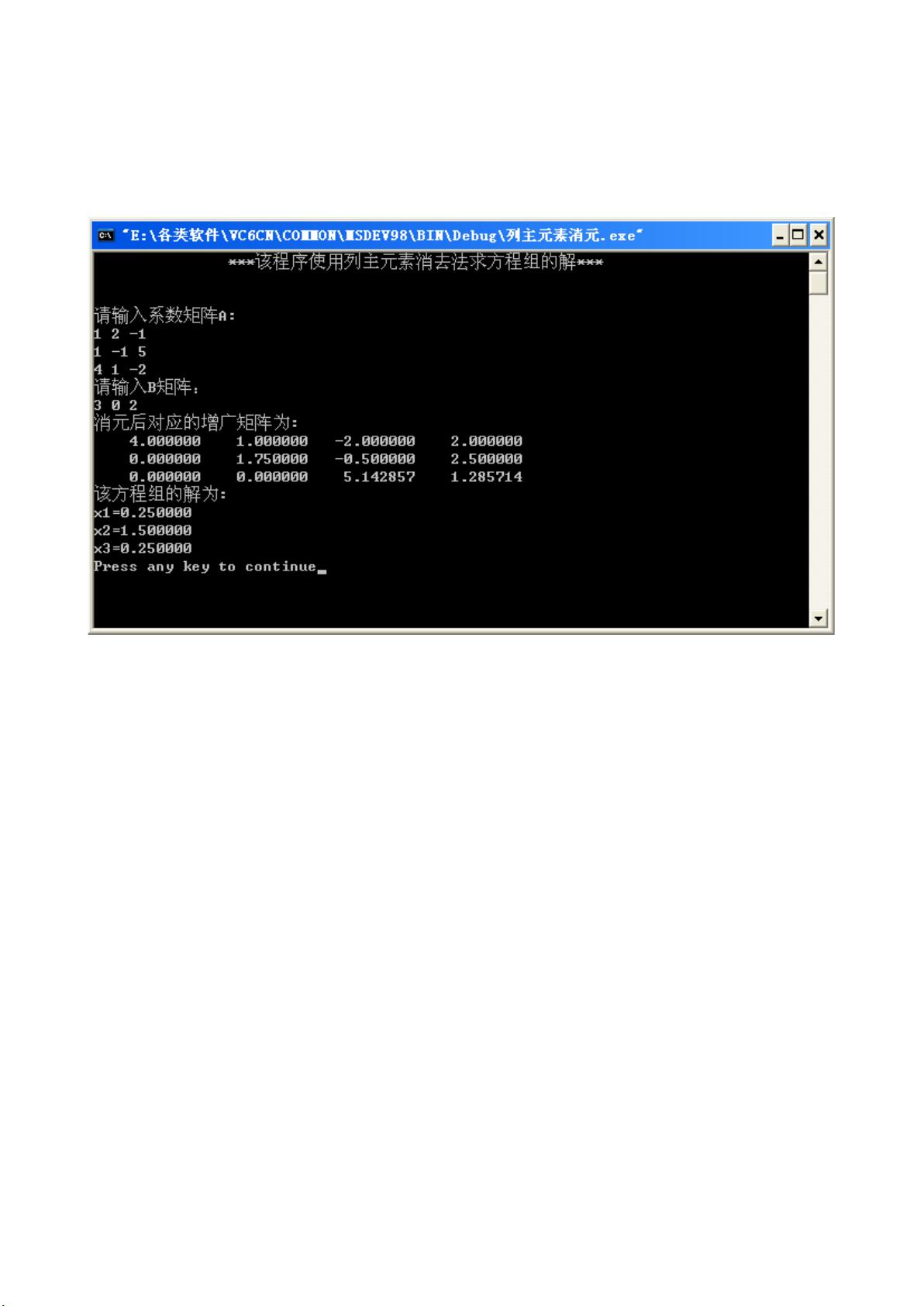
"这个资源包含一系列用C语言实现的数值分析算法，如gauss消去法，列主元素消去法，doolittle分解法，平方根分解法，追赶法，Jacobi迭代法，Gauss-Seidel迭代法，SOR迭代法，以及Romberg求积法和复合梯形、simpose、cotes求积法。这些算法主要用于解决线性方程组求解和数值积分问题。" 数值分析是数学的一个分支，主要研究如何用数值方法来解决数学问题，特别是在计算机上进行数值计算。C语言是一种强大的编程语言，适合编写高效且精确的数值计算程序。 1. **高斯消去法**（Gauss Elimination）：这是一种基本的解线性方程组的算法，通过一系列行操作将系数矩阵转化为阶梯形矩阵，然后通过回代求解未知数。在给出的代码中，`gauss`函数实现了这一过程，而`huidai`函数则负责回代求解。 2. **列主元素消去法**（Row Echelon Form with Pivot Column）：此方法在高斯消去法的基础上，选择每一步的主元（非零且绝对值最大的元素）作为除数，以减少计算中的数值误差。 3. **Doolittle分解法**：用于将矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积，常用于求解稀疏矩阵问题。 4. **平方根分解法**（Square Root Factorization）：这是一种特殊的矩阵分解方法，对于某些类型的矩阵可能更为有效。 5. **追赶法**（Gaussian Elimination with Partial Pivoting）：为了避免高斯消去法中可能出现的较大或较小的分母，采用部分主元选择策略，即每次选取当前位置列中的最大绝对值元素作为主元。 6. **雅可比迭代法**（Jacobi Iteration）：适用于对角占优的线性系统，通过迭代逐步接近解，每个迭代步长由对角元素确定。 7. **高斯-塞德尔迭代法**（Gauss-Seidel Iteration）：雅可比迭代法的改进版，每次迭代时使用当前已更新的值，收敛速度通常快于雅可比法。 8. **SOR（Successive Over-Relaxation）迭代法**：在高斯-塞德尔迭代的基础上，引入松弛因子，进一步加速收敛。 9. **Romberg求积法**：一种高精度的数值积分方法，通过组合不同步长的梯形规则积分结果，利用Richardson外推来提高精度。 10. **复合梯形规则、辛普森规则、科特斯规则**：都是数值积分的方法，用于近似计算函数的定积分。复合规则是将区间细分后分别应用基础积分规则（如梯形或辛普森规则），然后将结果相加，以提高精度。 这些算法在科学计算、工程问题和数据分析中有着广泛的应用，尤其是在无法得到解析解的情况下。学习和掌握这些方法，可以提升解决实际问题的能力。