C语言实现线性表与多项式表示及其操作详解

线性表在计算机科学中是一种基础的数据结构，它是一系列元素的有序集合，其中每个元素都有一个唯一的索引或者位置。在这份关于线性表及其实现的材料中，我们主要关注的是如何使用C语言来设计和操作线性表，特别是针对多项式的表示和操作。 1. **多项式表示**： - 多项式是数学中一种重要的数据结构，用于表示形式为 \( a_0 + a_1x + a_2x^2 + \ldots + a_nx^n \) 的函数，其中 \( n \) 是项数，\( a_i \) 是系数，\( x \) 是变量。在计算机中，我们需要有效地存储多项式项的信息，包括项数 \( n \)，系数 \( a_i \) 和对应的指数 \( i \)。 - **方法1：顺序存储（数组）**： - 通过数组直接表示多项式，每个数组元素对应多项式的一个项，如 \( a[i] \) 表示 \( x^i \) 的系数。例如，多项式 \( 1 - 3x^2 + 4x^5 \) 可以用数组表示为 [1, -3, 0, 0, 4]，非零项的下标与指数相对应。 - **方法2：顺序存储（结构数组）**： - 对于非零项，采用 (系数, 指数) 的二元组形式存储，可以节省空间并保持有序，如 \( (9, 12), (15, 8), (3, 2) \)。这种方法使得多项式按指数大小进行排序，便于后续的计算操作。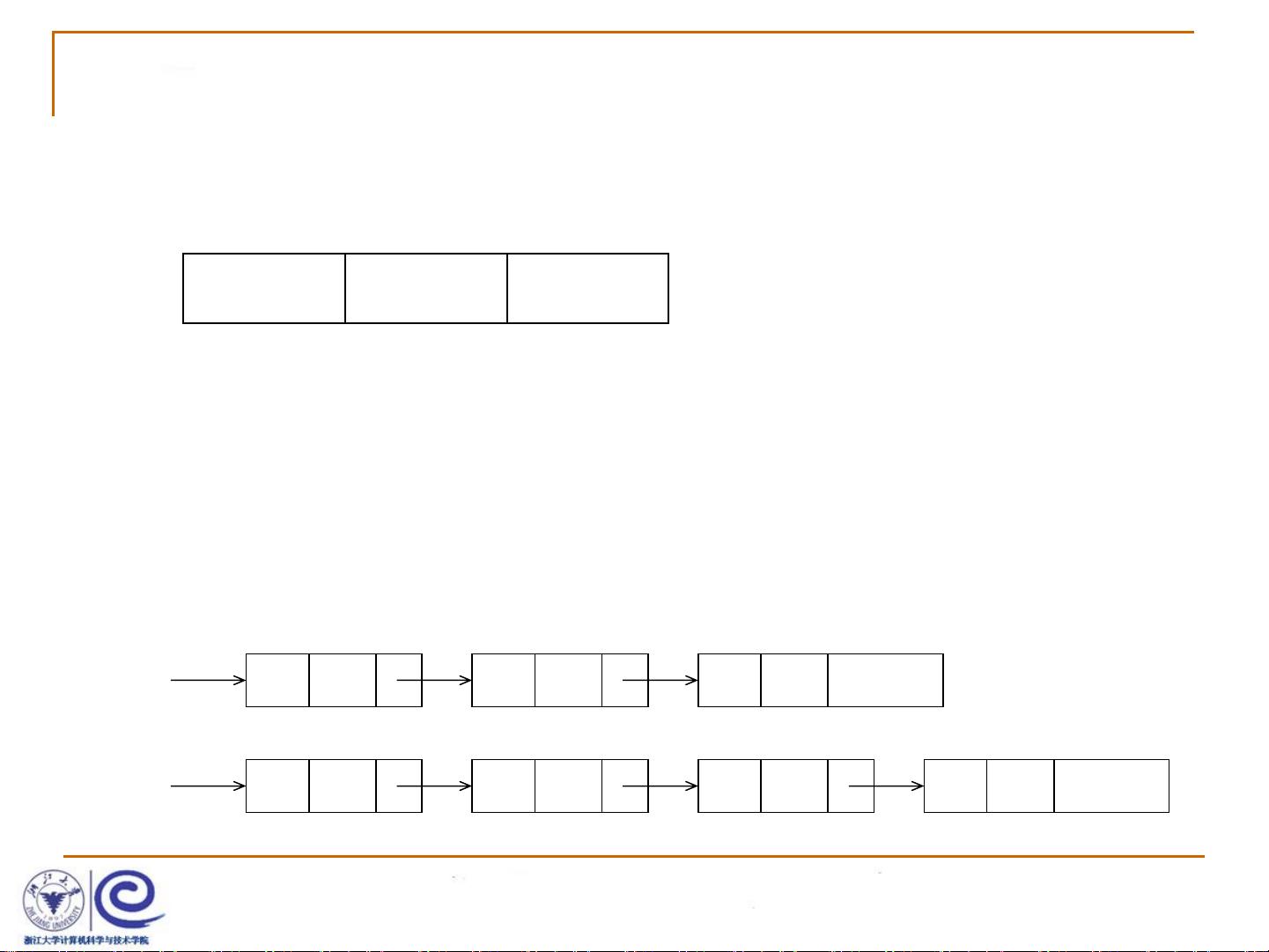 - **方法3：链表存储**： - 这种方式使用链表结构，每个节点包含一个多项式项，包括系数（coef）、指数（expon）和指向下一个项的指针（link）。这使得存储更为灵活，插入和删除操作效率较高，但查找可能较慢。 - **示例**： - 对于多项式 \( x + 3x^{2000} \)，可以用方法2表示为一个有序的二元组集合，或者用链表存储为一系列结构体节点，其中每个节点代表一个非零项。 2. **多项式运算**： - 主要的运算包括多项式相加、相减和相乘。在方法2的有序存储中，相加过程从头开始比较指数，然后依次添加对应的系数。链表存储则允许灵活地处理这些操作，比如通过遍历链表节点逐个计算。 这份资源提供了三种不同的线性表实现方式，适用于不同场景下的多项式处理。理解并熟练掌握这些方法对于编程者来说是非常有价值的，尤其是在处理需要存储和操作有序数据集的算法和数据结构问题时。通过C语言的具体实现，学习者可以加深对线性表概念的理解，并掌握其实现细节。