等腰直角三角形全等证明及其应用实例

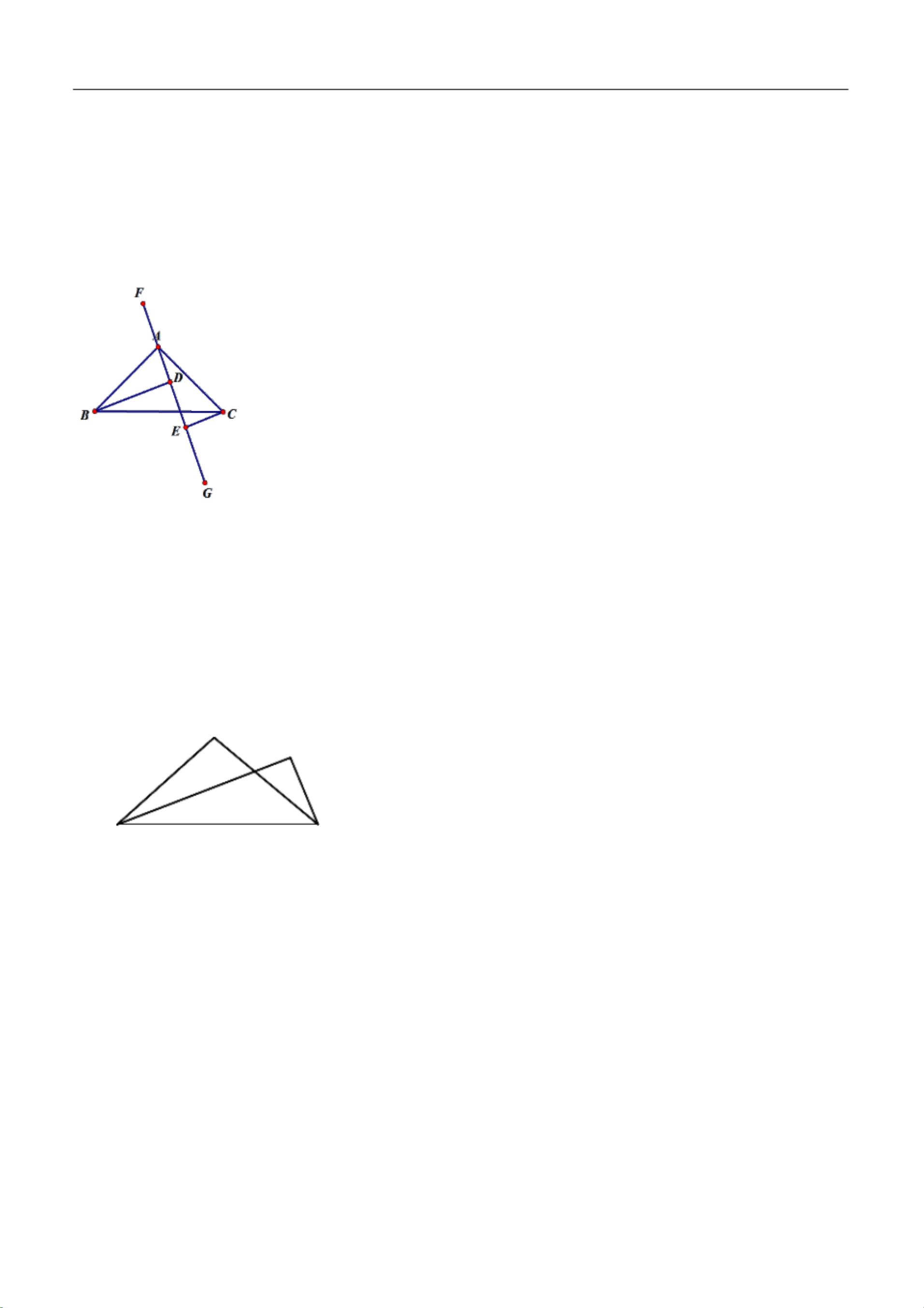
等腰直角三角形的全等问题是一系列涉及这类特殊三角形的几何证明题，这些题目主要利用了等腰直角三角形的特性，如两腰相等、一个直角以及它带来的角度关系。在证明三角形全等的过程中，关键在于识别并利用等腰直角三角形的对称性、直角边的等长以及角的关系。 例如，问题2中，通过过顶点作垂线构造辅助线，利用了等腰三角形的性质和垂直平分线的性质，证明DE等于BD减去CE，这是因为两个小三角形ABD和CAE因为AB=AC而全等，从而得出边长的关系。 问题3和4都涉及到角平分线的应用，通过构建全等三角形来简化证明。在第三个问题中，BD平分∠ABC，通过延长CE并与BA的延长线交于F，利用角平分线性质和平行线的性质，证明了CE等于BD的一半。而在第四个问题中，通过平行线和垂线的性质，证明了EF与DF所在的三角形全等，进而得出EF等于DF。 问题5和6则是综合应用等腰直角三角形和相似三角形的知识。在等腰直角三角形ACD和AEB中，因为两个三角形都有90度角且边长关系已知，可以通过旋转或相似比来解决边长求解的问题。比如，问题6中，通过逆时针旋转CA，使得CA与BA重合，然后利用AD和CD的长度，结合等腰直角三角形的性质，求出BD的长度。 这些题目展示了如何巧妙地利用等腰直角三角形的特性进行证明，并通过构造全等三角形、利用对称性和相似关系，有效地解决了三角形之间的全等关系，进而求解边长或其他几何量。理解和掌握这类问题的解法，对于深入理解几何定理和证明技巧具有重要意义。