遗传算法在函数优化中的应用示例

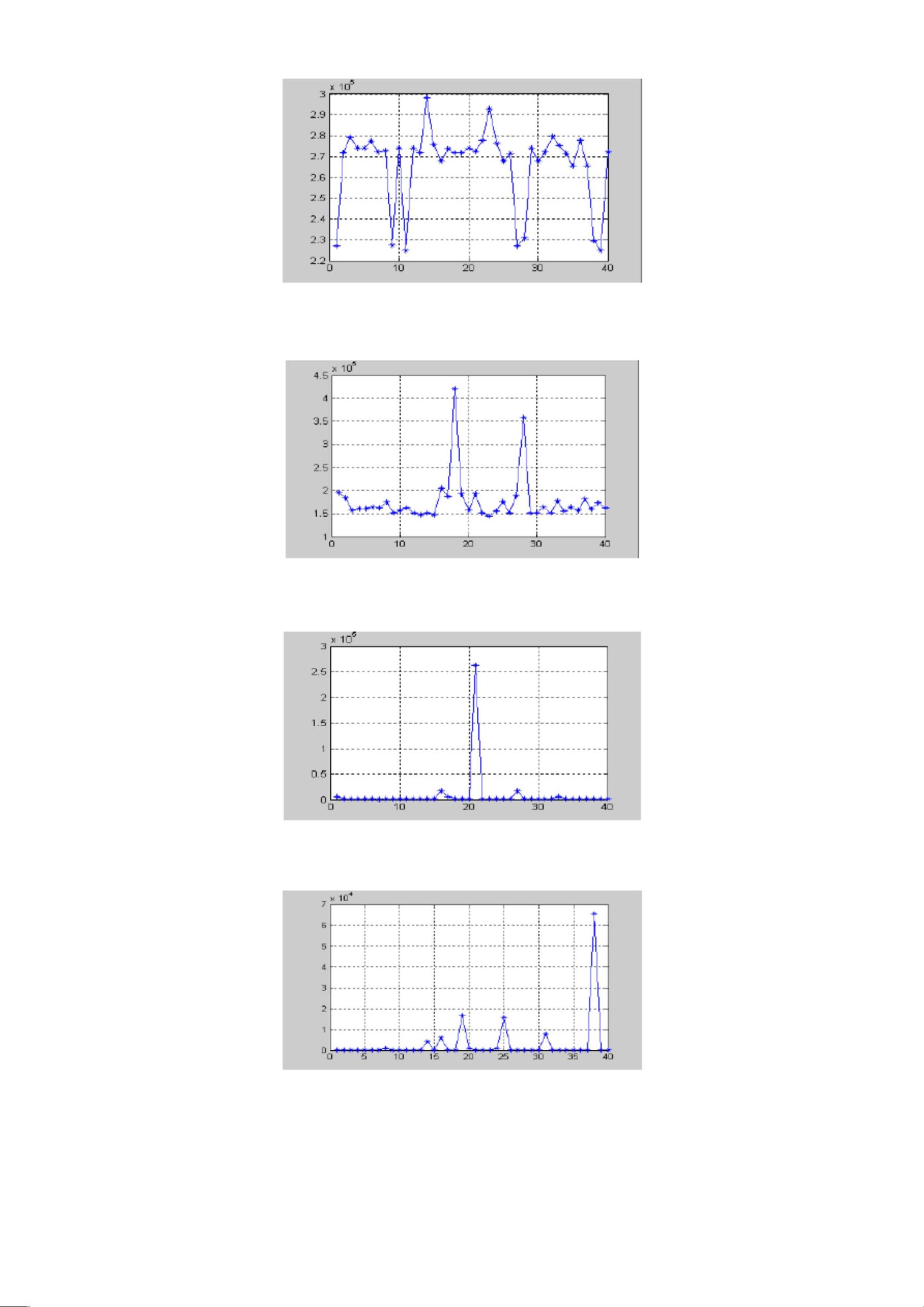
"该文档是关于遗传算法在实际问题中的应用示例，主要涉及一元函数优化的问题。通过MATLAB程序展示了如何运用遗传算法来寻找给定函数的最大值。" 在第七章“遗传算法应用举例”中，我们探讨了遗传算法在解决复杂优化问题上的广泛应用。遗传算法是一种基于生物进化原理的全局优化方法，它可以处理非线性、多模态以及多目标问题，不受特定领域限制。随着对其深入研究，遗传算法已经被广泛应用到各个领域，如函数优化、组合优化、控制系统、机器人、图像处理、人工智能和机器学习等。 本章以一个简单的例子——一元函数优化为例，来解释如何使用遗传算法来寻找函数的最大值。给定的函数是f(x) = x*sin(10π*x) + 2.0，其中x的取值范围在[-1, 2]。为了实现这个优化过程，采用了二进制编码，设定种群大小为40，每个个体的长度为20，代沟（Genetic Gap）设置为0.9，最大遗传代数设为25。 MATLAB代码首先绘制了函数曲线，然后定义了遗传算法的关键参数，包括个体数目、二进制位数、代沟等。接下来，算法执行包括选择、重组和变异等步骤，以生成新的种群。在每一代结束时，会计算并存储最优解，同时更新适应度值。通过这种方式，遗传算法逐步逼近最优解，直到达到预设的代数上限。 在代码中，`select('sus', Chrom, FitnV, GGAP)` 表示使用选择策略（在这里是基于比例的选择策略，即"survival of the fittest"），`reins` 函数负责重组和变异操作，`max(ObjV)` 找到当前种群中目标函数的最大值，`plot(variable(I), Y,'bo')` 在函数图上标记最优解的位置。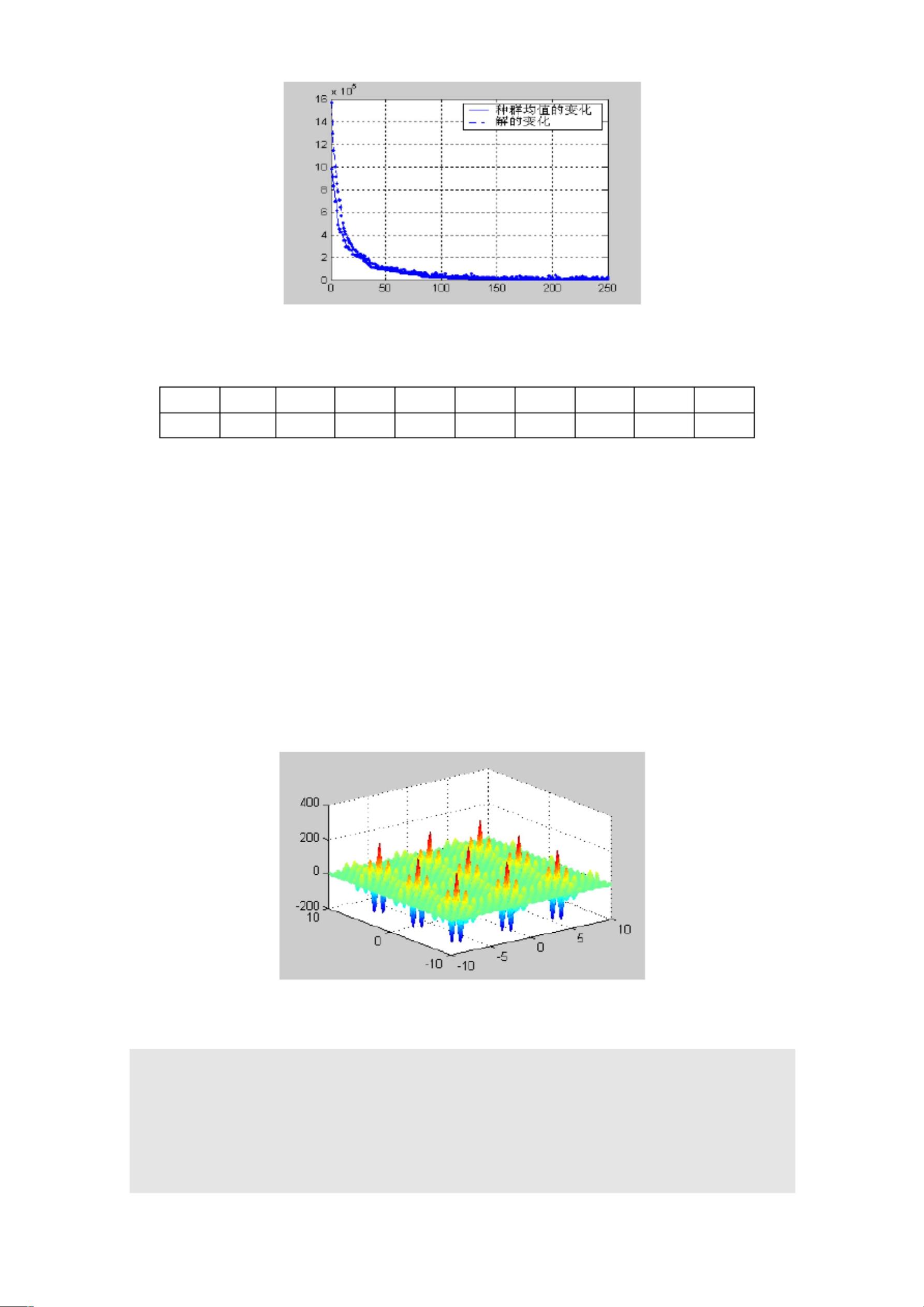 此外，代码还记录了每一代的平均目标函数值，用以评估算法的收敛性。最后，将最佳个体的解转换回十进制形式，并在图上用星号表示，同时绘制了平均目标函数值随代数变化的曲线，以显示算法的性能追踪。 这个例子充分展示了遗传算法在解决实际问题中的灵活性和有效性，通过编程实现了对复杂函数的优化，找出了全局最优解。这种方法可以扩展到更复杂的优化问题，为实际工程和科研提供了强大的工具。