Dijkstra算法在最短路问题中的应用

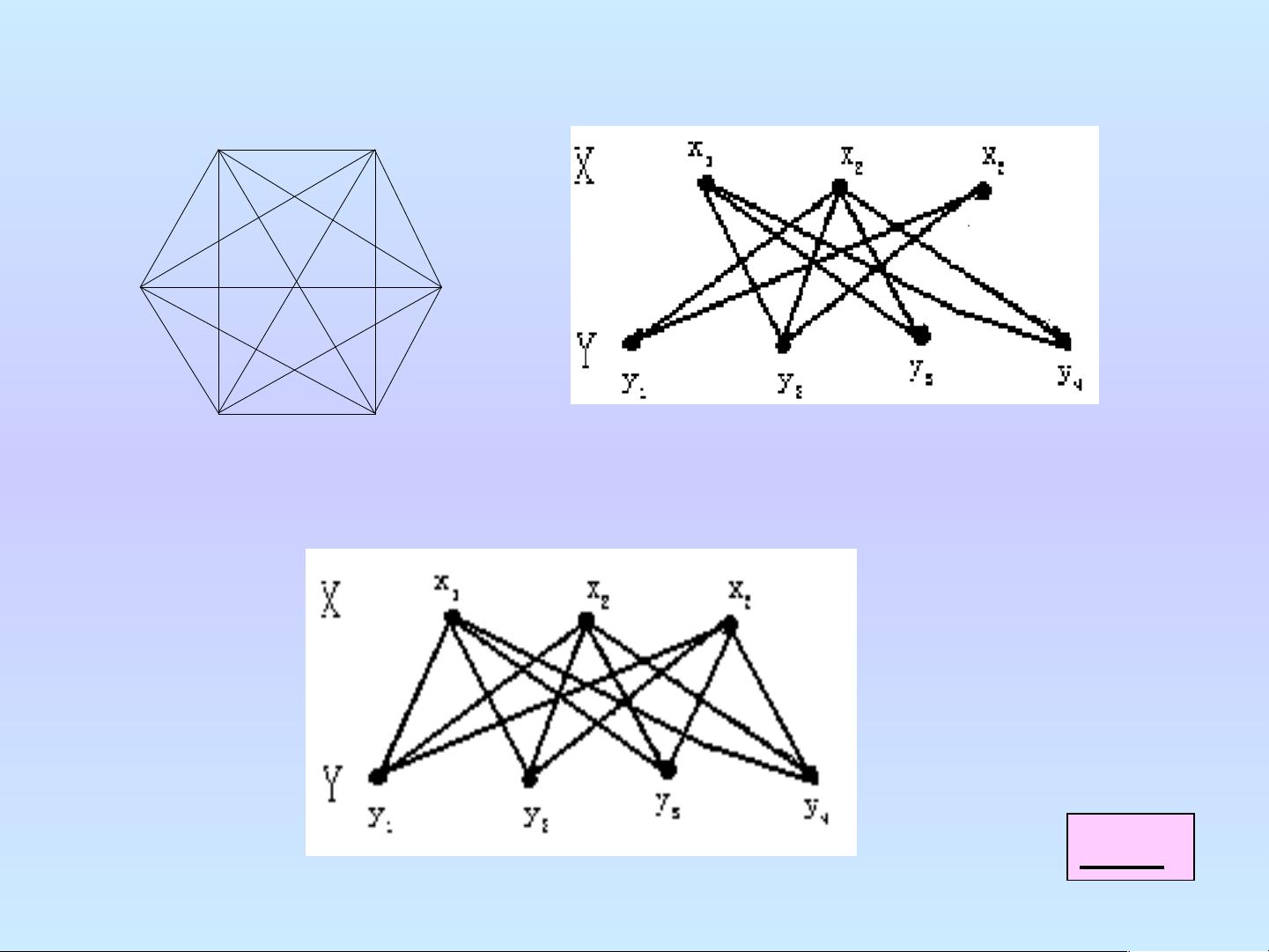
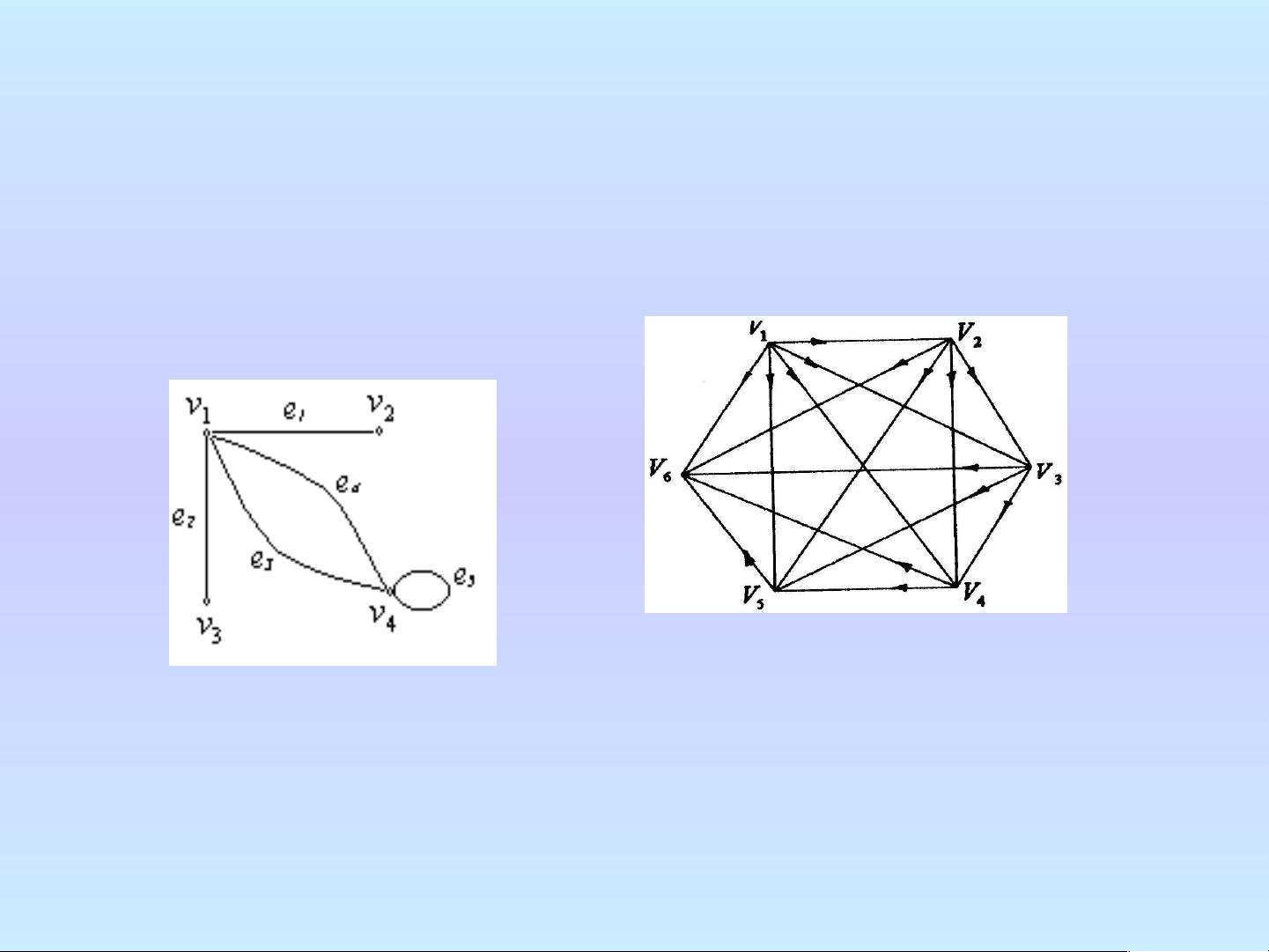
"起点与终点重合的路径称为圈．Dijkstra算法：求G中从顶点u0到其余顶点的最短路" 本文主要介绍的是图论中的基本概念和最短路问题，以及与之相关的算法。首先，我们要理解图的定义，一个图G由顶点集V、边集E和关联函数构成，可以是有向、无向或混合图。边可以带有权重，这样的图被称为赋权图。在图中，环是指起点和终点相同的边，即自环。重边则是指在同一对顶点间存在两条或多条边。 最短路问题是一个经典的图论问题，它寻找的是在图中从一个特定顶点（源点）到其他所有顶点的最短路径。Dijkstra算法是一种解决此类问题的有效方法，由荷兰计算机科学家艾兹格·迪科斯彻提出。该算法以源点u0为起点，逐步扩展最短路径，直到找到图中所有顶点的最短路径。Dijkstra算法的核心思想是使用优先队列（如二叉堆）存储待扩展的顶点，并保证每次选取当前未访问顶点中距离源点最近的一个。 实验内容包括了解最短路问题的算法及其应用，掌握使用Matlab软件求解最短路问题，以及学习图论的基本概念，如顶点的次数、子图、关联矩阵和邻接矩阵等。实验作业可能涉及实际问题的建模，例如最优截断切割问题，通过建立数学模型，利用最短路算法寻找最佳解决方案。 在图的矩阵表示中，关联矩阵和邻接矩阵是两种常用的方法。关联矩阵是将图中的边用0和1表示，无向图的邻接矩阵是对称的，而有向图的邻接矩阵则不一定。邻接矩阵则直接记录了图中每个顶点之间是否有边相连，对于赋权图，邻接矩阵的元素是边的权重。 最短路问题在很多领域都有应用，如网络路由、交通规划、物流配送等。理解并掌握这些基本概念和算法对于解决实际问题至关重要。在进行图的分析时，需要注意图的性质，如是否为简单图、完备图等，这会影响最短路算法的选择和计算过程。例如，如果图中存在环，某些算法可能无法正确找到最短路径，因此需要特别处理。同时，对于带权重的图，还需要考虑负权重边的情况，因为某些算法（如Dijkstra）并不适用于负权重边的图。