贪心算法详解：从活动安排到最优化问题

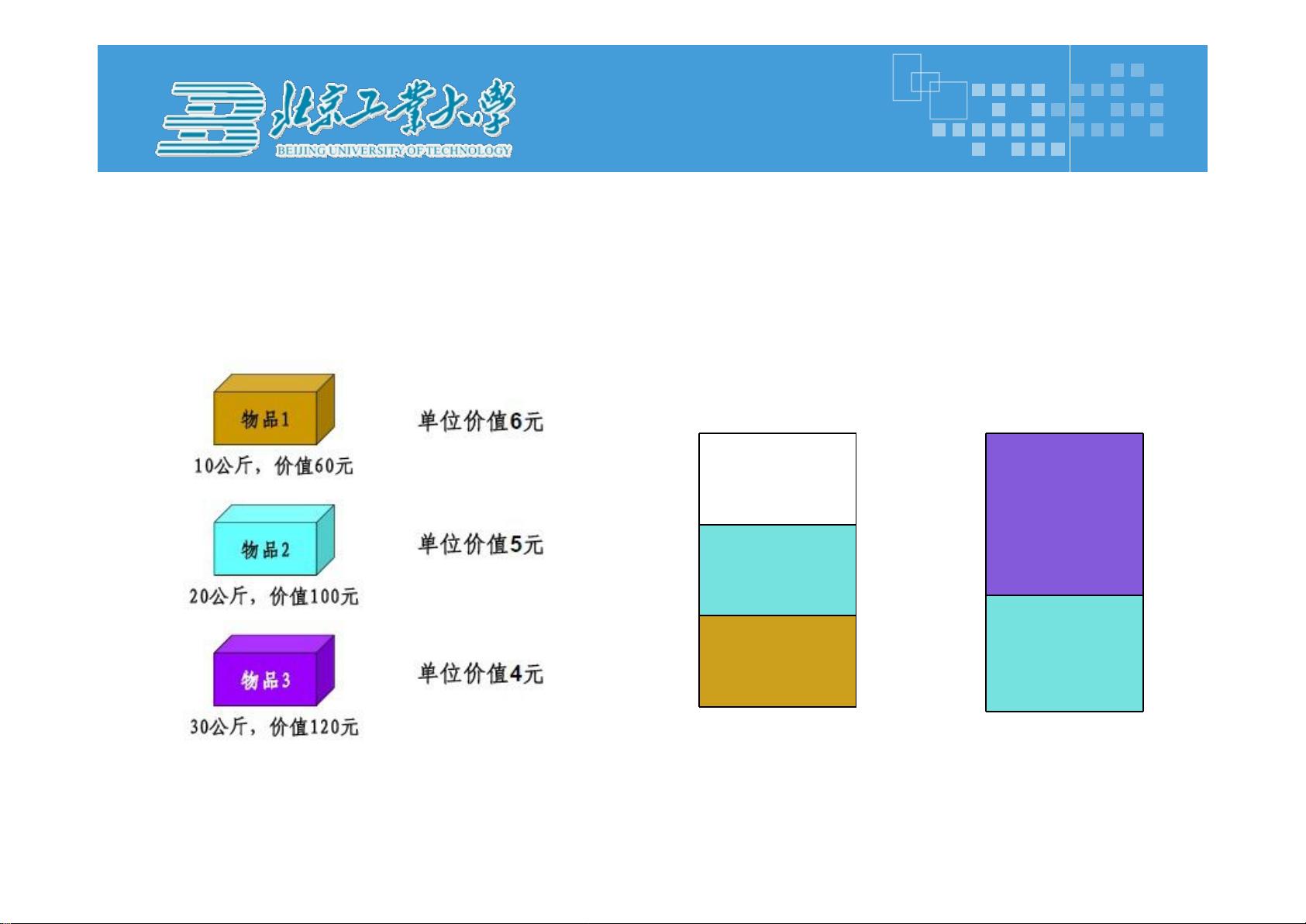
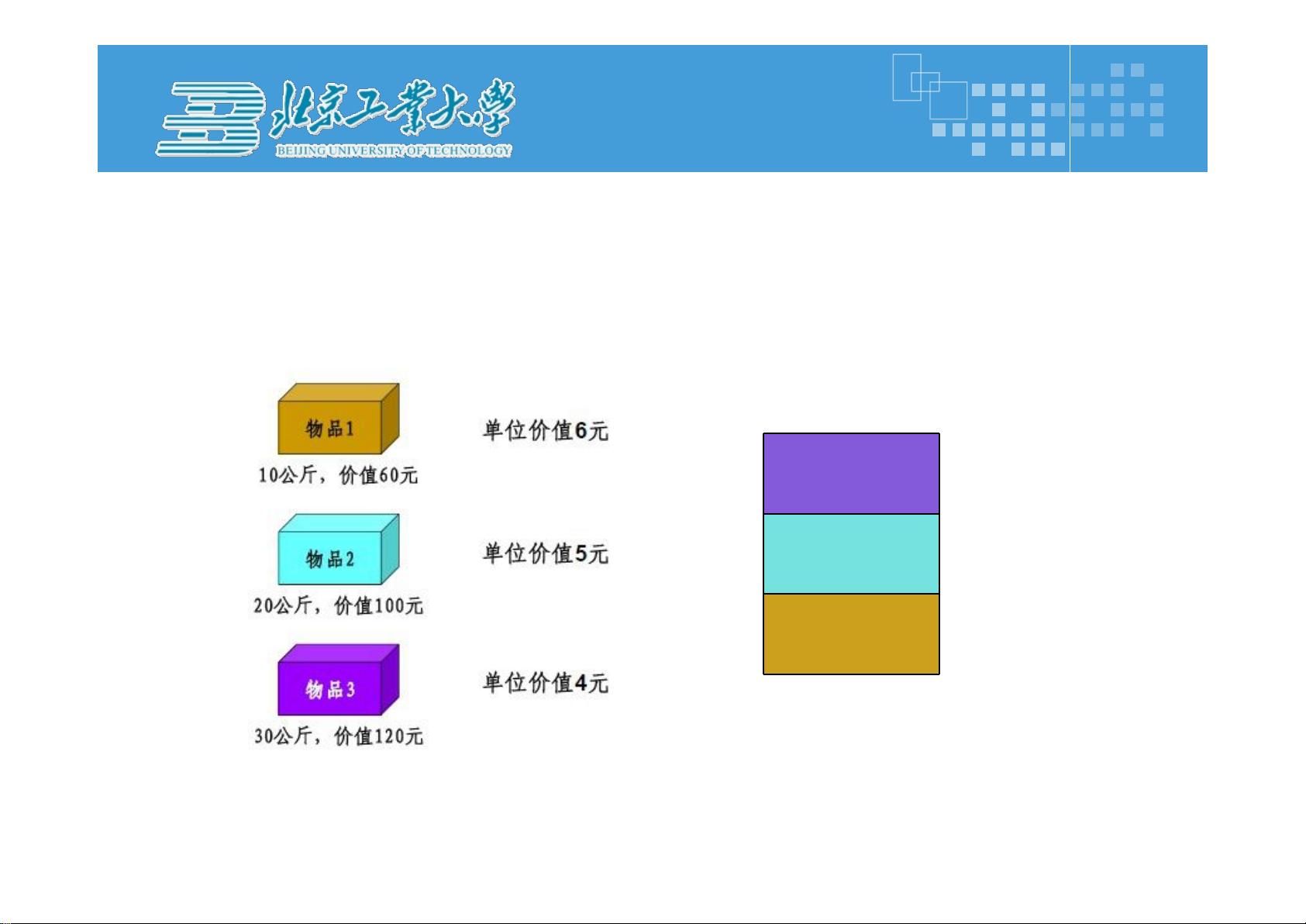
"这篇文档是关于《算法分析与设计》的第三讲，主要讨论了贪心算法的概念和应用。贪心算法是一种解决问题的方法，它在每个步骤中都选择当前看起来最优的解决方案，而不一定考虑全局最优。" 在计算机科学中，贪心算法是一种求解优化问题的有效策略，尤其在面对具有局部最优解性质的问题时。这种算法的核心思想是每次做出局部最优决策，希望通过这些局部最优的累积达到全局最优的状态。尽管贪心算法不能保证对所有问题都能找到全局最优解，但它在某些特定问题上，如霍夫曼编码、单源最短路径、最小生成树等，能够找到整体最优解。 文档提到了几个具体的贪心算法应用实例： 1. **活动安排问题**：例如，如果有多个活动需要在有限的资源或时间上安排，贪心算法会选择最早结束的活动优先，这样可以尽可能多地安排活动。 2. **最优装载问题**：在货物装载问题中，贪心算法可能会选择重量最大的货物先装，以期望在有限的空间内装载更多的货物。 3. **单源最短路径**：Dijkstra算法就是一种典型的贪心算法，它每次选择距离起点最近的未访问节点，逐步构建最短路径树。 4. **哈夫曼编码**：哈夫曼编码利用贪心策略构建最小带权路径长度的二叉树，从而实现数据的高效压缩。 5. **多机调度问题**：在多台机器上分配任务时，贪心算法可能会选择执行时间最短的任务优先，以期尽快完成所有任务。 6. **付款问题**：如文档中所述的找零问题，贪心策略是每次都选取面值最大的货币，直到凑足所需金额，以此减少找零的货币数量。 贪心算法通常包括以下步骤： 1. 初始化解（solution）为空。 2. 对于输入集合中的每一个元素，选择一个合适的元素（x）。 3. 检查当前选择的元素（x）是否与已有的解（solution）兼容，即是否满足可行条件。 4. 如果可行，将选择的元素加入到解中。 5. 重复步骤2至4，直到所有输入元素都被处理。 然而，贪心算法的关键在于正确地定义局部最优选择，并确保这些局部最优的组合能够导致全局最优解。在实际应用中，设计贪心算法需要仔细分析问题特性，确保局部最优解能导向全局最优解。如果问题的最优解可以通过局部最优解的组合获得，那么贪心算法就是一种非常有用的工具。