压缩采样基础：从少数样本恢复信号

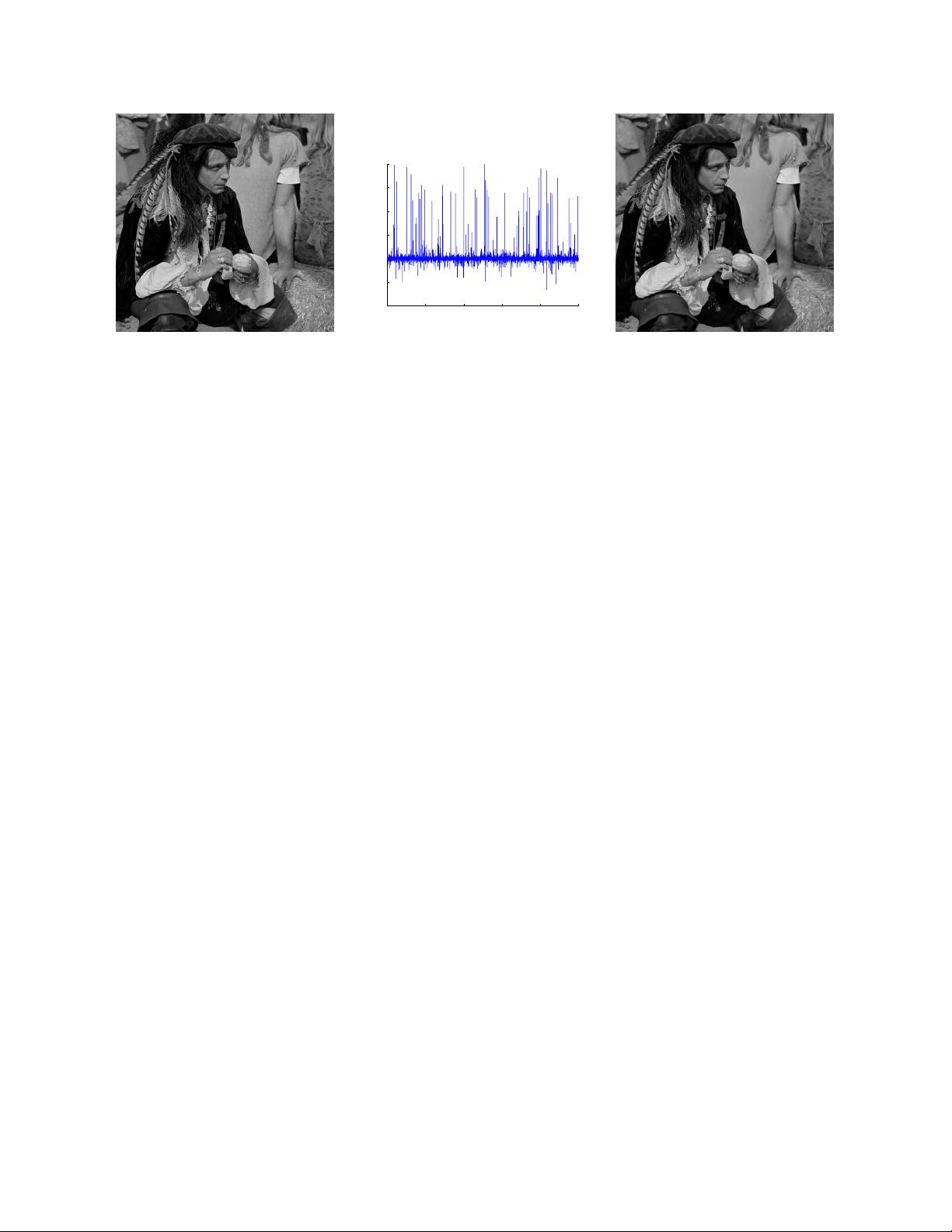
"这篇论文概述了压缩采样，也称为压缩感知或CS，这是一种与传统数据采集观念相反的新颖采样/传感范式。压缩感知理论认为，可以从比传统方法少得多的样本或测量中恢复某些信号和图像。实现这一目标的关键在于两个原则：稀疏性和不相关性。稀疏性涉及感兴趣信号的特性，而不相关性则涉及传感模式。" 在介绍部分，论文提出了对信号采样的传统理解是基于香农采样定理：采样率至少应为信号中最高频率的两倍（即奈奎斯特定理）。这在消费类音频和视频电子设备、医学成像设备、无线电接收器等领域的信号获取协议中几乎无处不在。例如，在数据转换领域，标准的模拟到数字转换器(ADC)技术就遵循均匀采样或超过奈奎斯特速率的量化香农表示。 然而，压缩采样理论挑战了这一常规观念。它指出，对于满足特定条件的信号，可以通过非均匀或随机的方式进行低速率采样，并仍然能够重构原始信号。这种条件主要涉及信号的稀疏性和测量系统的不相关性。 稀疏性是指信号可以在某个基或变换域内表示为大部分元素为零，只有少数几个元素非零。这些少数非零元素代表信号的主要特征。例如，在图像处理中，图像可能在频域或小波域中表现出稀疏性。 不相关性则是指测量系统与信号之间的关系。理想的压缩感知系统应该设计得与信号的稀疏基不相关，这样可以确保采样过程中不会丢失关键信息。不相关性使得即使采样点数量较少，也能有效地捕获信号的全部信息。 压缩感知的理论基础包括随机矩阵理论、优化算法以及信号恢复的理论。它利用线性代数中的正交性概念，如范数最小化问题，来从有限的采样点中重建信号。例如，通过最小化L1范数（也称为L1回归或稀疏最小化）可以鼓励解决方案的稀疏性。 此外，论文还可能探讨了实际应用中的压缩感知，如在MRI成像中减少扫描时间、无线通信中的频谱效率提升、以及大规模数据集的高效处理。这些应用展示了压缩采样如何在保持重构质量的同时，降低硬件成本、提高速度和降低能量消耗。 压缩采样提供了一种革命性的信号处理方法，通过改变我们对传统采样理论的认识，为解决实际工程问题提供了新的途径。它不仅在理论上具有重要意义，而且在实际应用中展现了巨大的潜力。