深度优先搜索与广度优先搜索算法详解

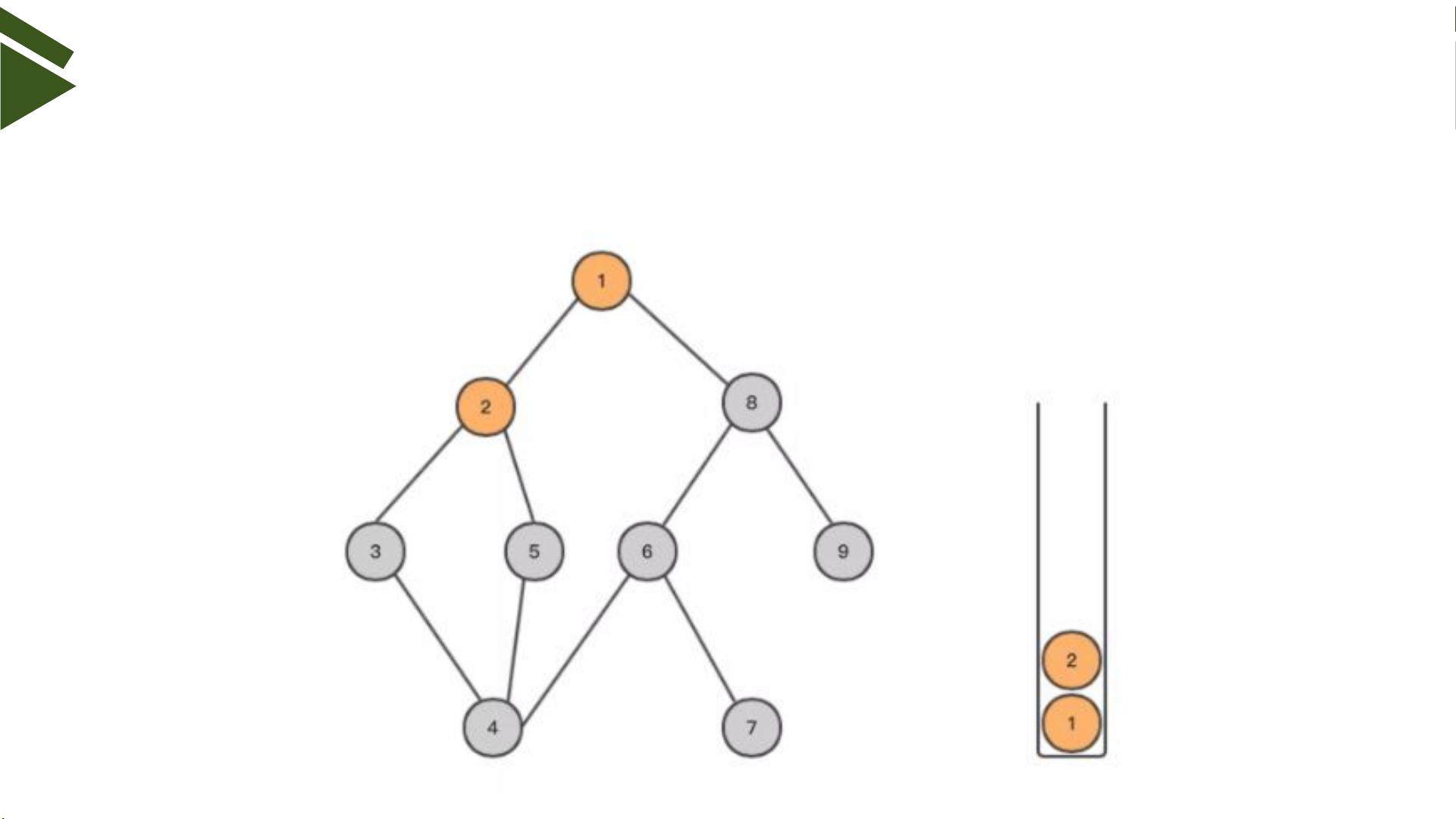
"DFS和BFS是两种常用的图遍历算法，主要应用于计算机科学和图论领域，尤其在解决路径寻找、最短路径等问题时。这两种算法分别基于深度优先和广度优先的策略进行节点的访问。" 深度优先搜索(DFS)是一种用于遍历或搜索树或图的算法。它沿着树的深度分支搜索树的节点，尽可能深地搜索树的分支。当节点v的所在边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。DFS通常使用栈或者递归来实现，可以产生目标图的拓扑排序。 在DFS过程中，基本步骤如下： 1. 从根节点开始，标记为已访问。 2. 探索与当前节点相邻且未被访问的节点，将其标记为已访问，并将该节点作为新的当前节点。 3. 如果当前节点没有未访问的邻接节点，回溯到上一个节点，继续探索其他分支。 4. 这个过程持续到所有节点都被访问。 DFS的核心代码示例： ```cpp void dfs(int st) { int i; printf("%d", st); for (i = 1; i <= n; i++) { if (vis[i] == 0 && a[st][i] == 1) { // 访问未访问的节点 vis[i] = 1; // 标记找过的节点 dfs(i); // 递归查找 } } return; } ``` 广度优先搜索(BFS)则是另一种图遍历算法，它从根节点开始，按照层次顺序访问节点，即先访问所有距离源节点近的节点，然后再访问较远的节点。BFS通常使用队列来实现。在Dijkstra单源最短路径算法和Prim最小生成树算法中，BFS思想起到了关键作用。 BFS的基本过程： 1. 将根节点放入队列。 2. 当队列不为空时，取出队首节点，访问它，然后将它的所有未访问邻居加入队列。 3. 重复上述步骤，直到队列为空，所有节点都被访问。 DFS和BFS各有优势，DFS在某些情况下可以节省空间，但可能会导致较长的运行时间；而BFS则常用于寻找最短路径，因为它总是先访问离起点近的节点。选择哪种算法取决于具体的问题和需求。