分支限界算法实现与最短路径问题

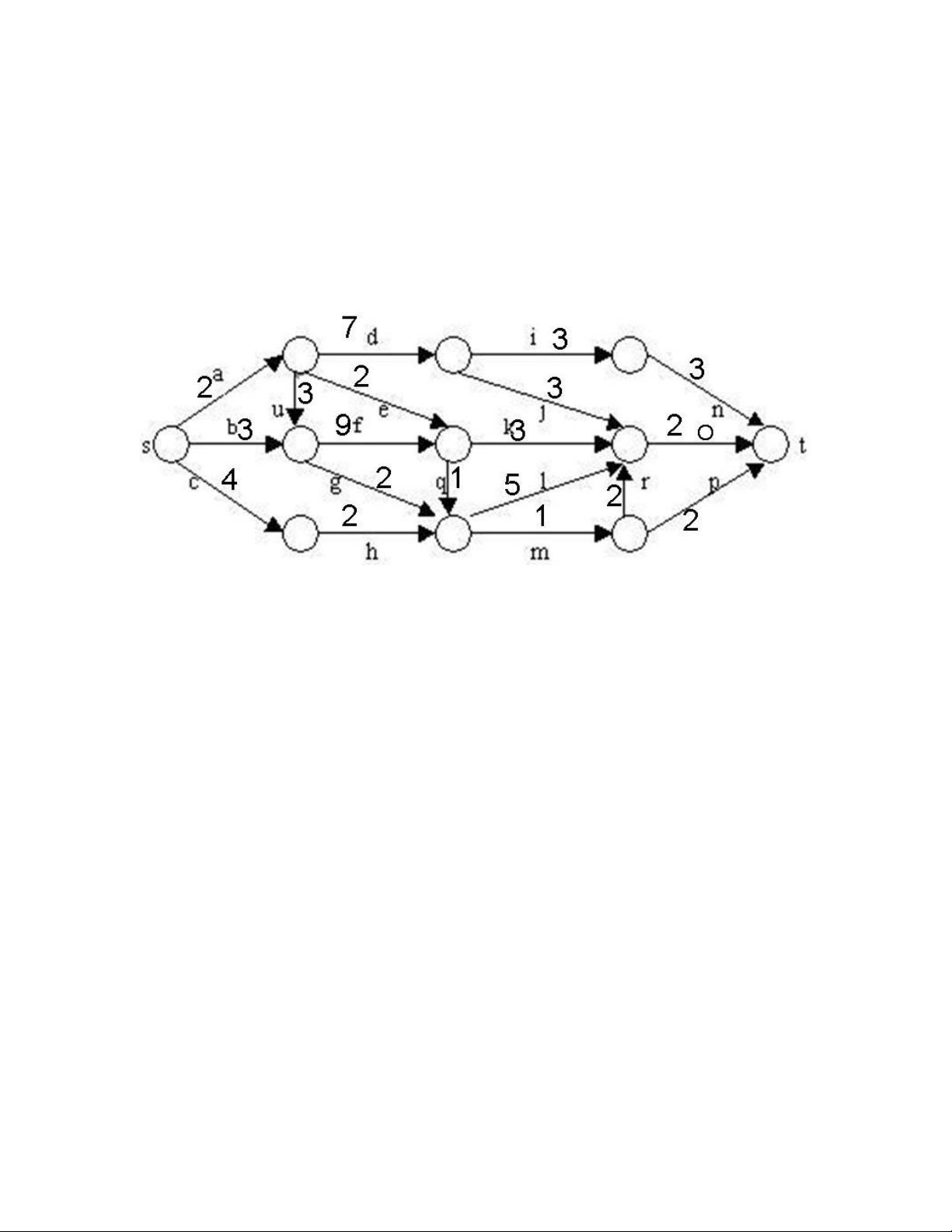
"该资源是关于分支限界算法的一个实测代码示例，具体应用是在有向图中寻找从源顶点s到目标顶点t的最短路径问题。" 分支限界算法是一种用于求解优化问题的有效方法，它通过系统地枚举问题的解空间树来寻找最优解。在这个过程中，算法会按照一定的策略（通常是广度优先或最小耗费优先）扩展节点，并在扩展过程中不断剪枝，排除那些不可能导致最优解或无解的子树，以提高搜索效率。 在这个代码实现中，问题被定义为寻找有向图中的一条从源顶点s到目标顶点t的最短路径。图的每个边都具有非负权重，代表从一个顶点到另一个顶点的代价。代码使用了`node_info`结构体来存储节点的信息，包括节点的索引和权重。同时，`path_info`结构体用来记录路径的前一个节点索引和当前路径的总权重。 `ss_shortest_paths`类是实现分支限界算法的核心部分，它接收一个表示图的邻接矩阵`graph`以及目标节点的索引`end_location`作为输入。类中包含了计算最短路径的方法，并有一个`print_spaths`成员函数用于打印找到的最短路径及其权重。 代码中，`node_info`的比较操作符重载使得`priority_queue`可以按照权重从小到大的顺序排列节点，这符合最小耗费优先的搜索策略。在搜索过程中，每次从活结点表（在这里是优先队列）中取出权重最小的节点进行扩展，并更新最短路径信息。 整个算法执行的过程是：从源节点s开始，将其添加到活结点表中，然后不断取出权重最小的节点，检查是否到达目标节点或产生更短路径的节点，若找到则更新最短路径，否则继续扩展其他节点。当活结点表为空或者找到目标节点时，算法结束。 总结起来，该代码实现了一个基于分支限界算法的求解有向图中最短路径的问题，采用最小耗费优先的策略，通过优先队列进行节点的选取和扩展，有效地找到了从源节点到目标节点的最短路径。