彩色算法指南：经典问题解决与应用详解

需积分: 9 180 浏览量更新于2024-07-20 收藏 3.21MB PDF 举报

《图着色算法指南与应用》是一本由R.M.R.刘易斯编著的专业书籍，旨在深入探讨和介绍图着色算法及其在现实生活中的应用。这本书是针对计算机科学、运筹学、数学和工程等研究生课程设计的，它支持在线的一套图着色算法实现，这些算法是用C++编写的，确保了读者能够接触到最新的算法解决方案。图着色是一个经典问题，涉及将图形中的节点分配不同的颜色，以便任何相邻节点都不共享相同颜色，这在解决诸如座位安排、体育联赛组织以及大学课程表安排等实际问题时具有重要意义。作者通过本书详细介绍了几种高效的图着色算法，包括但不限于贪心策略、分支定界法、回溯法等，这些都是理论研究和实践应用中的关键技术。书中不仅涵盖了基本原理和理论，还包含了对复杂性分析的讨论，比如NP完全性，这对于理解算法的效率边界至关重要。此外，书中还可能包含一些启发式方法，如近似算法，它们能够在实际应用中提供较快的求解速度，尽管可能无法保证全局最优解。《图着色算法指南与应用》一书不仅提供了理论深度，而且还配以实例和案例研究，使读者能够更好地理解和掌握这些算法在不同场景下的运用。例如，通过模拟真实的座位安排问题，学生可以学习如何优化空间利用，减少冲突；而在体育比赛组织中，如何通过最小化颜色冲突来创建公平的比赛日程。本书的出版信息包括Springer Cham、Heidelberg、New York、Dordrecht和London等地的印刷版本，以及电子版，方便全球范围内的读者获取。版权方面，作者保留所有权利，强调了在没有特定许可的情况下，对作品的翻译、复制、传播、电子适应和软件使用等方面的要求。《图着色算法指南与应用》是一本实用而深入的资源，不仅适用于学术研究，也适合对图论和优化感兴趣的从业者，它提供了丰富的知识和实践经验，是提升计算机科学和相关领域技能的重要参考书籍。

4 1 Introduction to Graph Colouring

is friends with D, but can be assigned to the second. Continuing this process for all

eight students gives us the solution shown in Figure 1.3(b). This solution uses four

groups, and also involves student F being assigned to a group by himself.

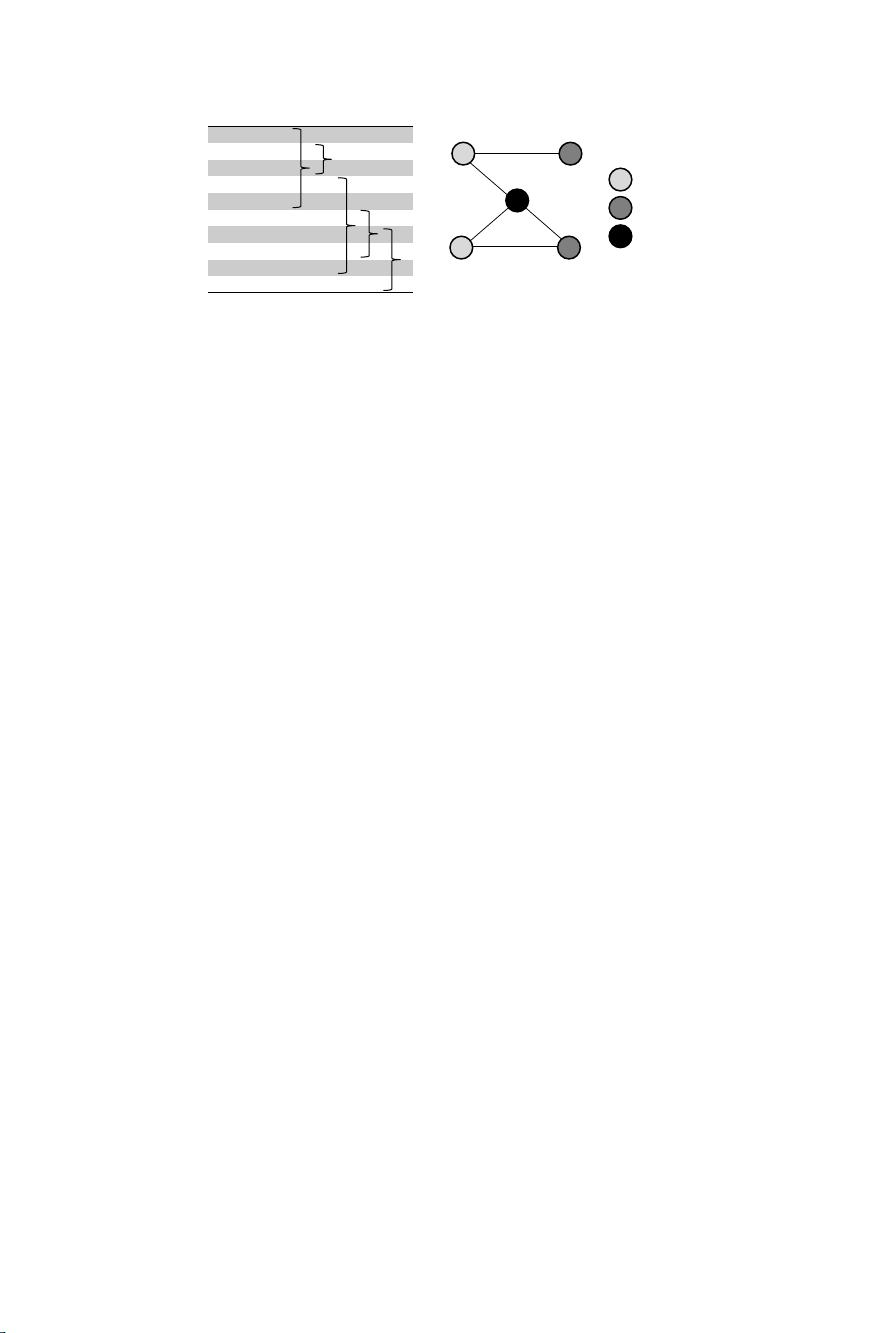
Can we do any better than this? By inspecting the graph in Figure 1.3(a), we

can see that there are three separate cases where three students are all friends with

one another. Speciﬁcally, these are students A, B, and C; students B, E, and F; and

students D, E, and F. The edges between these triplets of students form triangles

in the graph. Because of these mutual friendships, in each case these collections of

three students will need to be assigned to different groups, implying that at least

three groups will be needed in any valid solution. However, by visually inspecting

the graph we can see that there is no occurrence of four students all being friends

with one another. This hints that we may not necessarily need to use four groups in

a solution.

In fact, a solution using three groups is actually possible in this case as Fig-

ure 1.3(c) demonstrates. This solution has been achieved using the same assignment

process as before but using a different ordering of the students, as indicated. Since

we have already deduced that at least three groups are required for this particular

problem, we can conclude that this solution is optimal.

The process we have used to form the solutions shown Figures 1.3(b) and (c) is

generally known as the G

REEDY algorithm for graph colouring, and we have seen

that the ordering of the vertices (students in this case) can inﬂuence the number of

colours (groups) that are ultimately used in the solution it produces. The G

REEDY

algorithm and its extensions are a fundamental part of the ﬁeld of graph colouring

and will be considered further in later chapters. Among other things, we will demon-

strate that there will always be at least one ordering of the vertices that, when used

with the G

REEDY algorithm, will result in an optimal solution.

1.1.2 Constructing Timetables

A second important application of graph colouring arises in the production of

timetables at colleges and universities. In these problems we are given a set of

“events”, such as lectures, exams, classroom sessions, together with a set of “times-

lots” (e.g., Monday 09:00–10:00, Monday 10:00–11:00 and so on). Our task is to

then assign the events to the timeslots in accordance with a set of constraints. One of

the most important of these constraints is what is often known as the “event-clash”

constraint. This speciﬁes that if a person (or some other resource of which there

is only one) is required to be present in a pair of events, then these events must

not be assigned to the same timeslot since such an assignment will result in this

person/resource having to be in two places at once.

Timetabling problems can be easily converted into an equivalent graph colouring

problem by considering each event as a vertex, and then adding edges between any

vertex pairs that are subject to an event clash constraint. Each timeslot available in

1.1 Some Simple Practical Applications 5

the timetable then corresponds to a colour, and the task is to ﬁnd a colouring such

that the number of colours is no larger than the number of available timeslots.

Timeslot 1

Event 1

Event 2

Event 7

Event 4

Event 5

Event 3

Event 9

Event 8

Event 6

(a) (b)

(c)

Fig. 1.4 A small timetabling problem (a), a feasible 4-colouring (b), and its corresponding

timetable solution using four timeslots (c)

Figure 1.4 shows an example timetabling problem expressed as a graph colouring

problem. Here we have nine events which we have managed to timetable into four

timeslots. In this case, three events have been scheduled into timeslot 1, and two

events have been scheduled into each of the remaining three. In practice, assuming

that only one event can take place in a room at any one time, we would also need

to ensure that three rooms are available during timeslot 1. If only two rooms are

available in each timeslot, then an extra timeslot might need to be added to the

timetable.

It should be noted that timetabling problems can often vary a great deal between

educational institutions, and can also be subject to a wide range of additional con-

straints beyond the event-clash constraint mentioned above. Many of these will be

examined further in Chapter 8.

1.1.3 Scheduling Taxis

A third example of how graph colouring can be used to solve real-world problems

arises in the scheduling of tasks that each have a start and ﬁnish time. Imagine that a

taxi ﬁrm has received n journey bookings, each of which has a start time, signifying

when the taxi will leave the depot, and a ﬁnish time telling us when the taxi is

expected to return. How might we assign all of these bookings to vehicles so that

the minimum number of vehicles is needed?

Figure 1.5(a) shows an example problem where we have ten taxi bookings. For

illustrative purposes these have been ordered from top to bottom according to their

start times. It can be seen, for example, that booking 1 overlaps with bookings 2, 3

and 4; hence any taxi carrying out booking 1 will not be able to serve bookings 2, 3

and 4. We can construct a graph from this information by using one vertex for each

booking and then adding edges between any vertex pair corresponding to overlap-

ping bookings. A 3-colouring of this example graph is shown in Figure 1.5(b), and

the corresponding assignment of the bookings to three taxis (the minimum number

possible) is shown in Figure 1.5(c).

6 1 Introduction to Graph Colouring

(a)

Tax i 1

Tax i 2

Tax i 3

(b)

(c)

Time Æ

Fig. 1.5 A set of taxi journey requests over time (a), its corresponding interval graph and 3-

colouring (b), and (c) the corresponding assignment of journeys to taxis

In this particular case we see that our example problem has resulted in a graph

made of three smaller graphs (components), comprising vertices v

to v

, v

to v

and v

to v

respectively. However, this will not always be the case and will depend

on the nature of the bookings received.

A graph constructed from time-dependent tasks such as this is usually referred to

as an interval graph. In Chapter 2, we will show that a simple inexpensive algorithm

exists for interval graphs that will always produce an optimal solution (that is, a

solution using the fewest number of colours possible).

1.1.4 Compiler Register Allocation

Our fourth and ﬁnal example in this section concerns the allocation of computer

code variables to registers on a computer processor. When writing code in a partic-

ular programming language, whether it be C++, Pascal, FORTRAN or some other

option, the programmer is free to make use of as many variables as he or she sees ﬁt.

When it comes to compiling this code, however, it is advantageous for the compiler

to assign these variables to registers

on the processor since accessing and updating

values in these locations is far faster than carrying out the same operations using the

computer’s RAM or cache.

Computer processors only have a limited number of registers. For example, most

RISC processors feature 64 registers: 32 for integer values and 32 for ﬂoating point

values. However, not all variables in a computer program will be in use (or “live”)

at a particular time. We might therefore choose to assign multiple variables to the

same register if they are seen not to interfere with one another.

Figure 1.6(a) shows an example piece of computer code making use of ﬁve vari-

ables, v

,...,v

. It also shows the live ranges for each variable. So, for example,

variable v

is live only in lines (2) and (3), whereas v

is live from lines (4) to (9).

It can also be seen, for example, that the live ranges of v

and v

do not overlap.

Hence we might use the same register for storing both of these variables at different

periods during execution.

Registers can be considered physical parts of a processor that are used for holding small pieces

of data.

1.2 Why “Colouring”? 7

(1)

← …

(2)

← …

(3)

… v

…

(4)

← …

(5)

… v

…

(6)

← …

(7)

← …

(8)

… v

…

(9)

… v

…

(10)

… v

…

Colour /

(a) (b)

Fig. 1.6 (a) An example computer program together with the live ranges of each variable. Here, the

statement “v

← ...” denotes the assignment of some value to variable v

, whereas “...v

...” is just

some arbitrary operation using v

. (b) shows an optimal colouring of the corresponding interference

graph

The problem of deciding how to assign the variables to registers can be modelled

as a graph colouring problem by using one vertex for each live range and then adding

edges between any pairs of vertices corresponding to overlapping live ranges. Such

a graph is known as an interference graph, and the task is to now colour the graph

using equal or fewer colours than the number of available registers. Figure 1.6(b)

shows that in this particular case only three registers are needed: variables v

and v

can be assigned to register 1, v

and v

to register 2, and v

to register 3.

Note that in the example of Figure 1.6, the resultant interference graph actually

corresponds to an interval graph, rather like the taxi example from the previous

subsection. Such graphs will arise in this setting when using straight-line code se-

quences or when using software pipelining. In most situations however, the ﬂow

of a program is likely to be far more complex, involving if-else statements, loops,

goto commands, and so on. In these cases the more complicated process of liveness

analysis will be needed for determining the live ranges of each variable, which could

result in an interference graphs of any arbitrary topology (see also Chaitin (2004)).

1.2 Why “Colouring”?

We have now seen four practical applications of the graph colouring problem. But

why exactly is it concerned with “colouring” vertices? In fact, the graph colouring

problem was ﬁrst noted in 1852 by a student of University College London, Fran-

cis Guthrie (1831–1899), who, while colouring a map of the counties of England,

noticed that only four colours were needed to ensure that all neighbouring counties

were allocated different colours.

To show how the colouring of maps relates to the colouring of vertices in a graph,

consider the example map of the historical counties of Wales given in Figure 1.7(a).

This particular map involves 16 “regions”, including 14 counties, the sea on the left

and England bordering on the right. Figure 1.7(d) shows that this map can indeed be

剩余255页未读，继续阅读

浮舟

粉丝: 627
资源: 381

彩色算法指南：经典问题解决与应用详解

A Guide to Graph Colouring

Graph Theory with Algorithms and its Applications

A Java Library of Graph Algorithms and Optimization - CRC Press

书：Comprehensive-Guide-to-Graph-Algorithms-in-Neo4j-ebook-EN-US.pdf

A Common-Sense Guide to Data Structures and Algorithms

Graph_algorithms

Graph-Algorithms

graph-algorithms

graph_algorithms

The Query-flow Graph - Model and Applications (2008)-计算机科学

最新资源