何晓飞教授讲解流形学习基础与理论

"何晓飞教授的流形学习讲解PPT" 流形学习是一种现代机器学习的方法，它基于数学中的流形理论，旨在从高维数据中发现低维的内在结构。流形学习的核心思想是，尽管实际数据可能存在于高维空间中，但这些数据往往具有较低维度的结构，即数据点可以近似地通过一个低维流形来描述。这个流形就像是高维空间中的一个曲面，尽管它可以复杂地弯曲，但局部上看起来像欧氏空间。 何晓飞教授，来自浙江大学，指出在信息时代，机器学习处理的问题通常涉及到数据集（Xi）和目标变量（Yi），它们都处于欧氏空间中。流形（Manifold）这个术语来源于拉丁语，意为“许多折叠”，形象地描述了多个曲面片的叠加但不相互拼接的几何形态。根据Whitney嵌入定理，任何流形都可以被嵌入到足够高的欧氏空间中。 流形假设是流形学习的基础，它认为真实世界的数据尽管在高维空间中分布，但具有低维的内在联系。比如，地球表面可以被视为一个二维流形，尽管在局部区域（例如一小片平地）可以近似看作二维的欧氏空间，但整体上它是一个弯曲的表面，具有非欧几里得几何特性。 流形的一个关键特征是它不满足欧几里得几何的平行公设。在球面上，不存在过任意两点的平行线，即测地线（大圆弧），它们会相交。此外，测地线用于计算流形上两点之间的最短路径，而测地三角形的内角和不一定等于180度，这与欧几里得平面中的情况不同。高斯在19世纪的测量实验就是对这种非欧几里得性质的早期实证研究。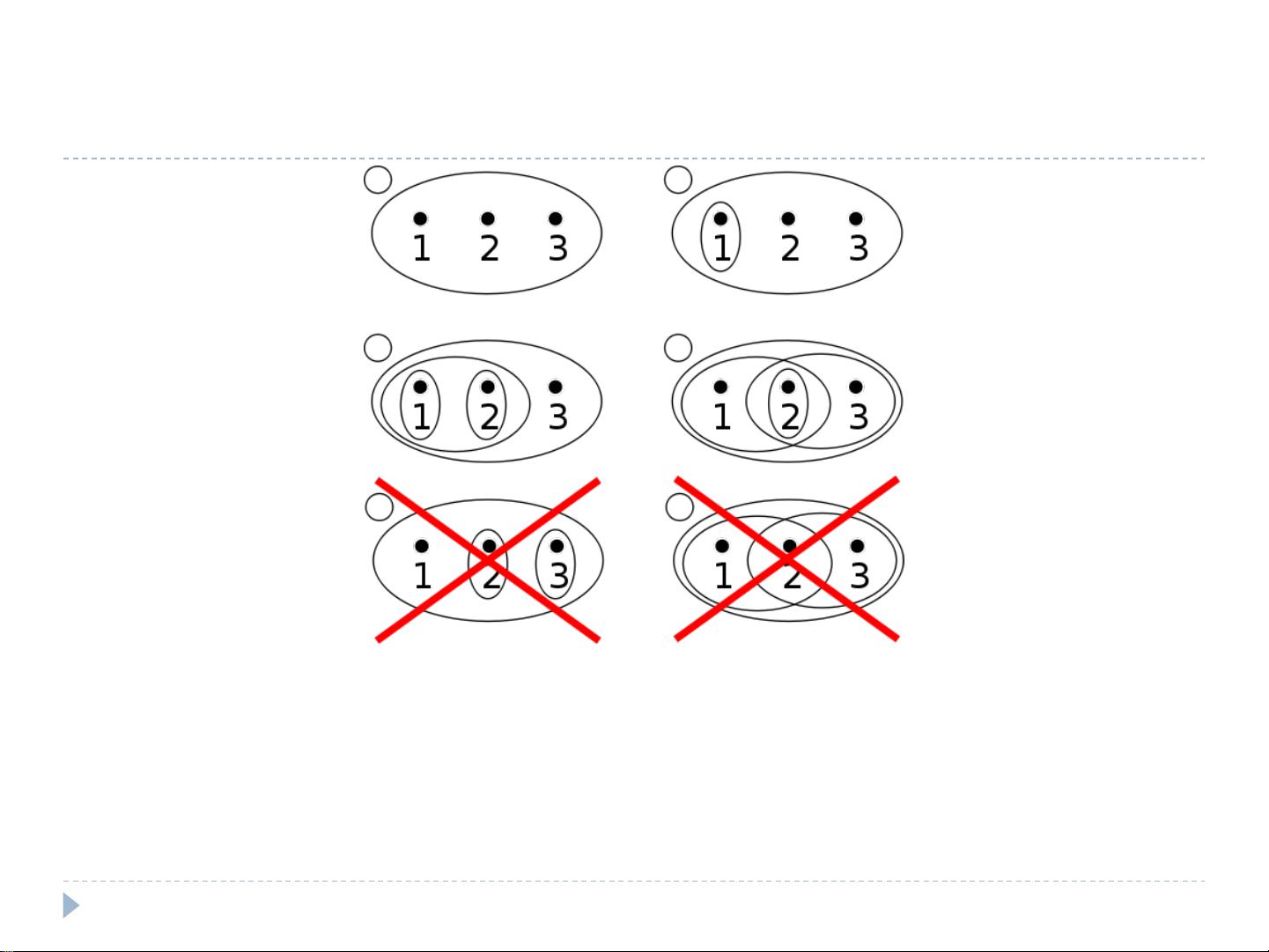 拓扑空间是理解流形的数学工具，它定义了一组集合的性质，如开集和闭集的行为，允许我们讨论连续性、连通性等概念。在拓扑空间中，集合X及其上的拓扑结构τ需满足特定的公理，包括空集和整个集合X都是开集，开集集合在任意并集下封闭，以及有限交集下也是封闭的。 流形学习的算法，如Isomap、LLE（局部线性嵌入）、MDS（多维尺度分析）和t-SNE（t分布随机邻域嵌入），都是试图在保持数据局部结构不变的情况下，将高维数据投影到低维空间，揭示隐藏的流形结构。这些方法在模式识别、图像处理、自然语言处理和复杂网络分析等领域有着广泛应用。