正交编码加BPSK与MFSK误码率性能仿真分析

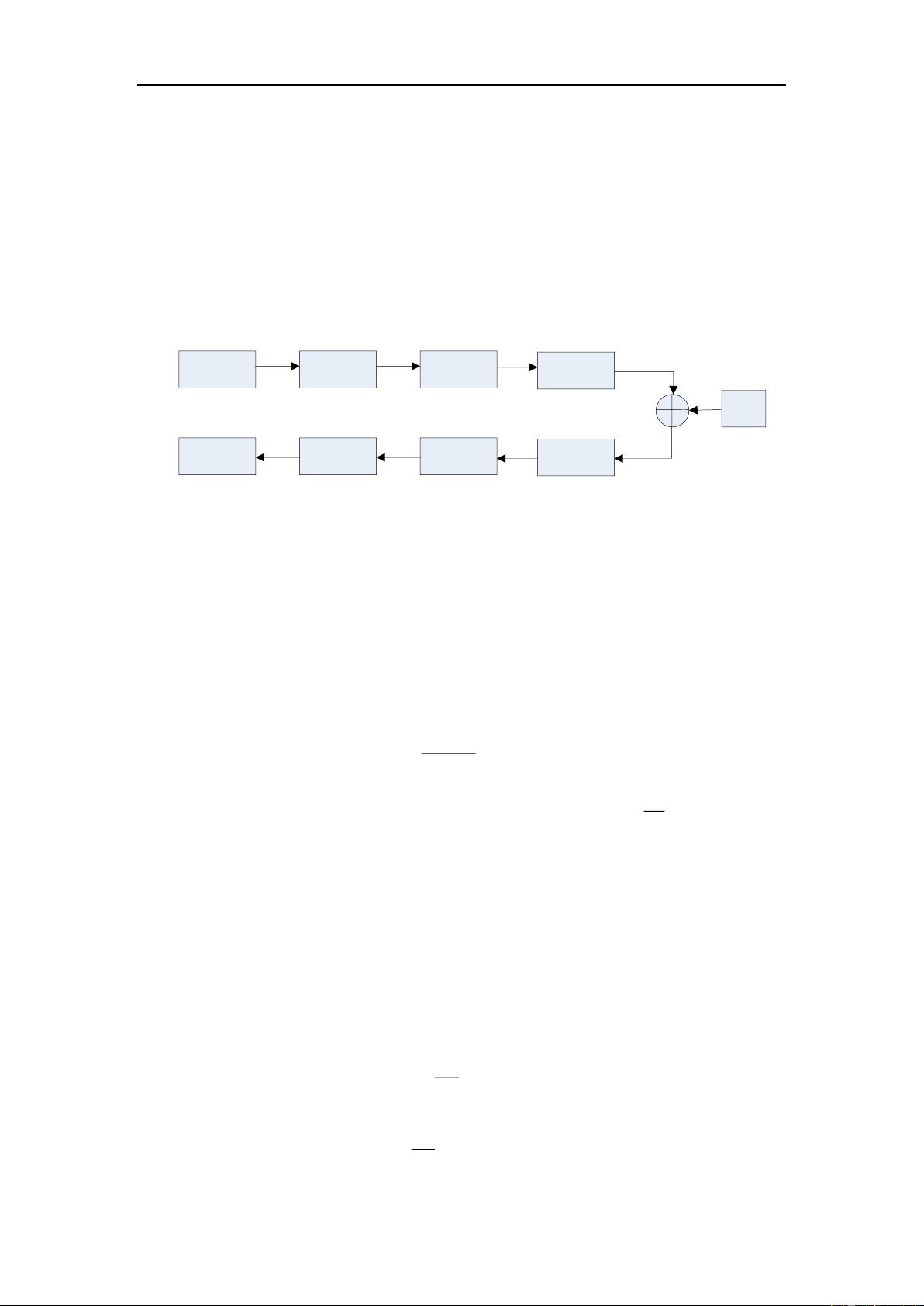
"正交编码加BPSK与MFSK性能仿真——通过理论分析和仿真实验，探讨了正交编码与BPSK及MFSK调制在误码率性能上的表现，证明M进制正交编码加BPSK与无编码的M进制正交FSK性能相同，可归结为M元正交波形传输系统。" 本文主要讨论了两种通信调制技术，即正交编码配合BPSK（Binary Phase Shift Keying）调制和MFSK（M-ary Frequency Shift Keying）调制的性能比较，并通过MATLAB仿真验证了它们的误码率（Bit Error Rate, BER）特性。首先，文章介绍了正交编码加BPSK的系统模型，该模型包括数字信源、正交编码、上采样、下采样、相关检测、BER统计以及在AWGN（Additive White Gaussian Noise，加性高斯白噪声）信道中的传输。 正交编码采用Hadamard矩阵，这是一种特殊构造的矩阵，其特点是行和列都是正交的，可以有效地将二进制序列转换为M阶正交序列，提高抗干扰能力。编码效率由公式(1.1)给出，即R_c = log_2(M) / M。接着，经过上采样，确保无码间干扰传输，这一过程通常会伴随根升余弦滤波器的应用，滤波器的参数如滚降系数和延迟会影响系统的性能。 在AWGN信道中，信号会受到随机噪声的影响，信噪比（SNR）与噪声功率N0和比特能量E_b的关系如公式(1.2)所示。相关检测用于从接收的信号中恢复发送序列，通过与M个正交序列进行相关运算找到最大相关值对应的序列，最后统计误码率以评估系统性能。 理论分析部分，文章给出了M元正交信号的误码率计算，使用了Q函数来描述在高斯噪声环境下的错误概率。Q函数是标准正态分布的累积分布函数的右尾部，它与误码率的计算密切相关。通过这种分析，可以验证仿真结果的正确性。 本文深入探讨了正交编码与BPSK调制结合在MFSK调制中的应用，通过理论与仿真相结合的方式，揭示了这两种调制方式在误码率性能上的相似性，为实际通信系统设计提供了重要的参考依据。