C语言实现的动力学中心差分法程序设计及其理论解析

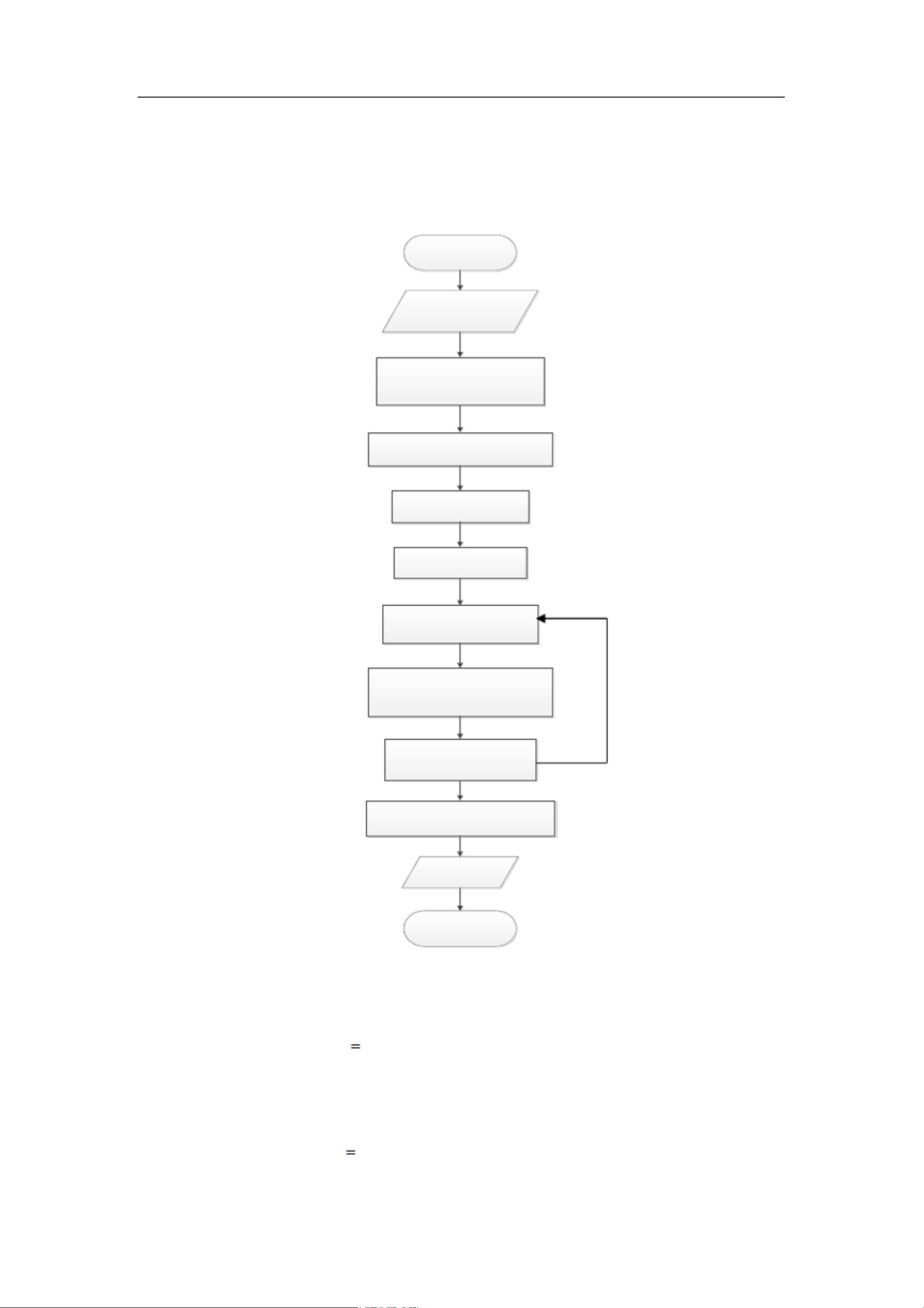
中心差分法是一种在动力学问题求解中常用的数值积分方法，它的基本理论与程序设计对于理解和应用有限元方法具有重要意义。本文档以C语言（部分C++语言）为基础，详细介绍了中心差分法在动力学问题中的应用以及其实现过程。 首先，程序设计的目的在于通过实践操作，巩固中心差分法的概念，提升实际编程能力。通过编写程序，参与者能够解决动力学问题，如位移、速度和加速度的求解，这在工程实践中具有很高的实用性。程序的特点在于计算简便，精度较高，尤其在处理连续时间动力学问题时，它避免了方程形式的变换，直接进行数值积分。 在动力学问题的数学表述中，系统由质量矩阵M、阻尼矩阵C、刚度矩阵K和节点载荷向量Q构成的方程组表示。动力分析相较于静力学，需要考虑惯性力和阻尼力，导致解不再是代数方程组，而是常微分方程组。中心差分法作为直接积分法的一种，核心思想是通过有限差分技术，用当前时刻的位移来近似计算速度和加速度，将微分方程转化为代数方程组的形式。这种方法的关键在于建立递推公式，通过在小的时间间隔内近似满足运动方程，逐次求解各时间步的位移变化。 具体来说，中心差分法的递推公式可以通过以下步骤得到：首先，将加速度和速度用时间步长内的位移表达，例如： \[ a(t) = \frac{u(t + h) - u(t)}{h}, \] \[ v(t) = \frac{u(t + h) - u(t - h)}{2h} \] 其中，u(t)是时间t的位移，h是时间步长。然后，将这些表达式代入运动方程的初始形式，得到： \[ M \frac{v(t + h) - v(t)}{h} + C \frac{u(t + h) - u(t)}{h} + K \frac{u(t + h) - 2u(t) + u(t - h)}{h^2} = Q \] 通过对以上方程的化简，可以得到求解下一个时间步位移的递推关系，从而求解整个动力学过程的位移、速度和加速度序列。这种方法不仅适用于单自由度系统，也扩展到了多体系统和复杂结构的分析，是数值仿真和结构动力学计算的重要工具。 这篇文档提供了中心差分法的核心理论及其在动力学问题中的程序实现，对于学习者深入理解有限元方法和数值求解技术具有重要的参考价值。通过阅读和实践，读者不仅能掌握这一方法，还能将其应用于实际工程项目，提升解决实际问题的能力。