数学分析（复旦大学数学系编）的答案

需积分: 5 66 浏览量更新于2023-03-03 评论 10 收藏 998KB PDF 举报

身份认证购VIP最低享 7 折!

领优惠券(最高得80元）

资源详情

资源评论

资源推荐

1˜Ÿ 4•Ø

1˜Ü© 4•ÐØ

1˜Ù Cþ†¼ê

§1. ¼êVg

1. )eØª§¿xÑx‰Œµ

(1) −2 <

x + 2

(2) (x − 1)(x + 2)(x − 3) < 0

(3)

x − 1

< a

(4) 0 6 cos x 6

(5)



− 16 < 0

− 2x > 0

)µ

(1) x < −

½x > −



-1-2-3

(2) 1 < x < 3½x < −2

 

-1-2 31 2

c cc

(3) a > 0ž§x < 1½x > 1 +



1 +

c c

a < 0ž§1 +

< x < 1

 

1 +

a = 0ž§x < 1



)µ

(1) ¼ê½Â••X = (−∞, 0)

(0, ∞)§f(−1) = 0, f (1) = 0, f(2) = −

(2) ¼ê½Â••X = [−|a|, |a|]§f(0) = |a|, f(a) = 0, f



−



√

|a|

(3) ¼ê½Â••(−∞, 0)

(0, ∞)§s(1) =

, s(2) =

(4) ¼ê½Â••



x ∈ R, x 6= kπ +

, k ∈ Z

§g(0) = 0, g





, g



−



= −

(5) ¼ê½Â••X = (−∞, ∞)§x



−



= −1, x(−π) = −1

(6) ¼ê½Â••X = (−∞, −2)

(−2, 1)

(1, +∞)§f(0) = −

, f(−1) = −

5. ¦e¼ê½Â•9Š•µ

(1) y =

√

2 + x − x

(2) y =

√

cos x

(3) y = ln



sin



(4) y =

sin πx

)µ

(1) ¼ê½Â••X = [−1, 2]§Š••





(2) ¼ê½Â••

2kπ −

, 2kπ +

(k ∈ Z)§Š••[0, 1]

(3) ¼ê½Â••



2k + 1



(k ∈ Z)§Š••(−∞, 0]

(4) ¼ê½Â••(n − 1, n)(n = 0, ±1, ±2, ···)§Š••(−∞, −1]

[1, +∞)

6. f(x) = x + 1, ϕ(x) = x − 2§Á)•§|f (x) + ϕ(x)| = |f(x) + |ϕ(x)|

)µd®•§f(x)ϕ(x) > 0=(x + 1)(x − 2) > 0§Kx > 2½x 6 −1.

7. f(x) = (|x| + x)(1 − x)§¦÷veˆªxŠµ

(1) f(0) = 0

(2) f(x) < 0

)µ

(1) ‡f(x) = 0§K|x| + x = 0½1 − x = 0§=x 6 0½x = 1

(2) Ï|x| + x > 0§K‡f(x) < 0§•‡1 − x < 0=Œ§=x > 1

8. ã1-5L«>³|V ! ½>{R

ÚŒC>{R|¤>´.3˜ãØ•žmS§A, Bü:m>ØV Œ±w

¤˜‡~þ.¦Ñ>6IÚŒC>{R¼êª.

)µd®•9ÔnÆ•£§V = I(R

+ R).

9. 3˜‡Î/NìS?,«M—§TÎ/Nì .Œ»´a§p•h§?M—pÝ´x£ã1-6¤. T

M—NÈV Úxƒm¼ê'XV = V (x)§¿Ñ§½Â•ÚŠ•.

)µd®•§V = πa

x§§½Â••[0, h]§Š••[1, πa

10. ,/Y± ¡È´˜‡F/§Xã1-7§.°2’§>–•45

§CDL«Y¡§¦¡ABCD¡

ÈS†Yh¼ê'X.

)µd®•9ã§S = h(h + 2).

11. k˜•H¶³§X^Œ»•RòÅ±z¦¨ωlÝ„Ýl¶³SåL-Ô§¦-Ô.¡†/¡

ålsÚžmt¼ê'X£ã1-8¤.

)µd®•9ã§s = H − ωRt



t ∈



ωt



12. y = f(x) =



1 + x

, x < 0

x − 1, x > 0

§¦f(−2), f(−1), f (0), f(1)Úf





)µd®•§f(−2) = 5, f (−1) = 2, f(0) = −1, f(1) = 0, f





= −

13. x(t) =







0, 0 6 t < 10

1 + t

, 10 6 t 6 20

t − 10, 20 < t 6 30

§¦x(0), x(5), x(10), x(15), x(20), x(25), x(30)§¿xÑù‡¼êã/.

)µd®•§x(0) = 0, x(5) = 0, x(10) = 101, x(15) = 226, x(20) = 401, x(25) = 15, x(30) = 20

14. e]y´&‡-þx¼ê.UìeÛ5½§éuIS×²&§U&‡-þ§z-20ŽAGe]8©§Ø

v20Žö±20ŽOŽ.&‡-þ360Ž±Sž§ÁÑù‡¼êLˆª§¿xÑ§ã/.

)µd®•§y = f(x) =







8, 0 < x 6 20

16, 20 < x 6 40

24, 40 < x 6 60

15. óÀu)ì)˜‡nÅ§ÙÅ/Xã1-9§Ñ¼ê'Xu = u(t)(0 6 t 6 20).

)µd®•9ã§u = u(t) =



1.5t, 0 6 t 6 10

30 − 1.5t, 10 < t 6 20

16. e¼êfÚϕ´Äƒ§•Ÿoº

(1) f(x) =

, ϕ(x) = 1

(2) f(x) = x, ϕ(x) =

√

(3) f(x) = 1, ϕ(x) = sin

x + cos

)µ

(1) Ïf½Â••(−∞, 0)

(0, +∞)§ϕ½Â••(−∞, +∞)§ùü‡¼êØƒ.

(2) Ïf(x) = x, ϕ(x) = |x|§ùü‡¼ê¼êLˆªØ˜§Kùü‡¼êØƒ.

(3) Ïϕ(x) = sin

x + cos

x = 1ð¤á§ùü‡¼êƒ.

17. y² éu †‚ ¼êf(x) = ax + b§ egCê Šx = x

(n = 1, 2, ···)|¤˜ê § Ké A¼ê

Šy

= f(x

)(n = 1, 2, ···)•|¤˜ê.

y²µx

m−1

, x

m+1

´x

¥?¿3‡ƒê(2 6 m 6 n)

âK¿§2x

= x

m−1

+ x

m+1

= f(x

) = ax

+ b§ Ky

m−1

= ax

m−1

+ b, y

= ax

+ b, y

m+1

= ax

m+1

+ b§ u ´2y

2ax

+ 2b, y

m+1

+ y

m−1

= ax

m+1

+ b + ax

m−1

+ b = 2ax

+ 2b§l2y

= y

m−1

+ y

m+1

m−1

, x

m+1

´x

¥?¿3‡ƒê§Ky

m−1

, y

m+1

´y

¥?¿3‡ƒê§u´y

= f(x

)(n =

1, 2, ···)•|¤˜ê.

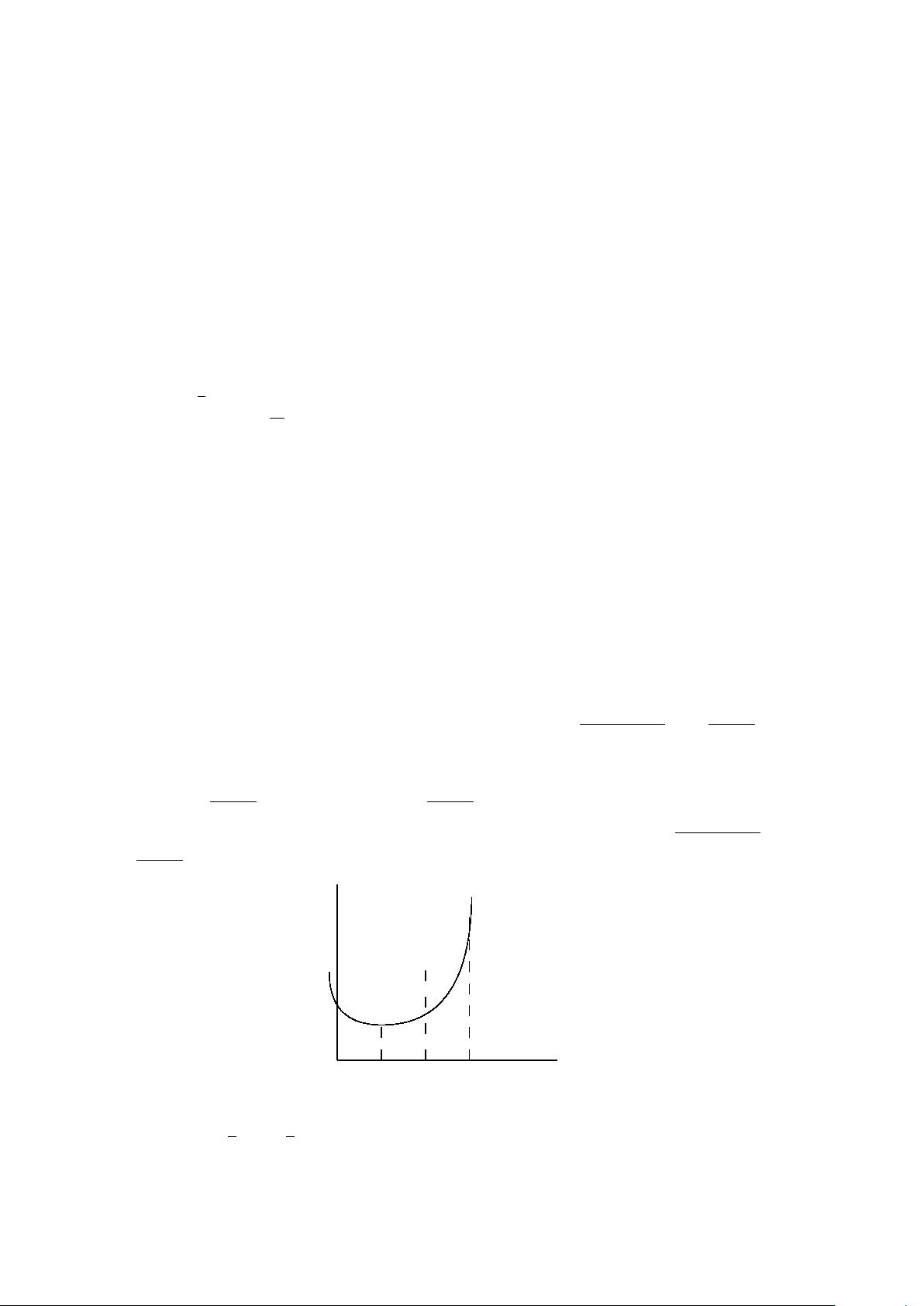
18. XJ-‚y = f(x)þ?˜^uÑpu§¤•l£ã1-10¤§y²Øª

f(x

) + f(x

)

> f



+ x



u¤kx

, x

6= x

)¤á£…äkþãA5¼ê‰à¼ê¤.

y ² µ 3-‚þ?ü:A(x

, f(x

)), B(x

, f(x

))§ëAB§Ù¥:C(x

, y

)§Kf(x

) + f (x

) =

, x

+ x

= 2x

q-‚þx

+ x

¤é:p‹I•y

= f



+ x



§Kx

= x

q-‚y = f(x)þ?˜^uÑpu§¤•l…x

, x

•u†l:§Ky

> y

f(x

) + f(x

)



+ x



éu¤kx

, x

6= x

)¤á.



f(x)

19. y²eˆ¼ê3¤««mS´üNO\¼êµ

(1) y = x

(0 6 x < +∞)

(2) y = sin x



−

6 x 6



y²µ

剩余102页未读，继续阅读

sdtsz

粉丝: 2
资源: 3

会员权益专享

数学分析（复旦大学数学系编）的答案

评论0

会员权益专享

最新资源

数学分析（复旦大学数学系编）的答案

评论0

复旦大学数学分析陈传璋课后答案

数学分析复旦 三版 答案

数学分析教材，复旦，陈传璋、金福临、朱学炎、欧阳光中编，带答案

2018复旦大学数学分析a期末

复旦大学数学分析b(i)考试卷

复旦大学泛函分析讲义pdf

复旦大学高数b期末试卷

如何联系复旦大学的招生办公室

复旦大学高数a期末试卷

复旦大学nlp数据集

复旦大学高等代数i期末考

复旦大学mse认可度

复旦大学统计与数据科学系

复旦大学模拟电路二级运放

复旦大学的mem专业怎么样

riscv三级流水线复旦大学

高等代数复旦第三版pdf

["清华大学经济学院", "北京大学法学院", "复旦大学管理学院",”百色学院经济学院”]修改为大学名称

hspice 语法 pdf 复旦

复旦大学的moss技术参数

会员权益专享

最新资源

数学分析复旦三版答案