没有合适的资源?快使用搜索试试~ 我知道了~
首页卷积神经网络研究综述_周飞燕.pdf
该文首先概述了卷积神经网络的发展历史,然后分别描述了神经元模型、多层感知器的结构.接着,详细分析了卷积神经网络的结构,包括卷积层、池化层、全连接层,它们发挥着不同的作用.然后,讨论了网中网模型、空间变换网络等改进的卷积神经网络.同时,还分别介绍了卷积神经网络的监督学习、无监督学习训练方法以及一些常用的开源工具.此外,该文以图像分类、人脸识别、音频检索、心电图分类及目标检测等为例,对卷积神经网络的应用作了归纳.卷积神经网络与递归神经网络的集成是一个途径.为了给读者以尽可能多的借鉴,该文还设计并试验了不同参数及不同深度的卷积神经网络来分析各参数间的相互关系及不同参数设置对结果的影响.最后,给出了卷积神经网络及其应用中待解决的若干问题. 知网论文,学习使用
资源详情
资源评论
资源推荐

书书书
第
40
卷
第
6
期
2017
年
6
月
计
算
机
学
报
CHINESE
JOURNAL
OF
COMPUTERS
Vol.40 No.6
June
2017
收稿日期
:
2016
-
07
-
27
;
在线出版日期
:
2017
-
01
-
18.
周飞 燕
,
女
,
1986
年 生
,
博 士 研 究 生
,
主要研究方向为计算机辅助心血管疾病诊断
.
E
-
mail
:
zhf
yy
f15
@
126.com.
金林鹏
,
男
,
1984
年生
,
博士
,
主要研究方向为机器学习
.
董
军
(
通信作者
),
男
,
1964
年生
,
博士
,
研究员
,
博
士生导师
,
主要研究领域为人工智能及其在健康监护
、
传统文化中的应用
.E
-
mail
:
j
don
g
2010
@
sinano.ac.cn.
卷积神经网络研究综述
周飞燕
1
),
2
)
金林鹏
1
),
2
)
董
军
1
)
1
)
(
中国科学院苏州纳米技术与纳米仿生研究所
江苏 苏州
215123
)
2
)
(
中国科学院大学
北京
100049
)
摘
要
作为一个十余年来快速发展的崭新领域
,
深度学习受到了越来越多研究者的关注
,
它在特征提取和建模
上都有着相较于浅层模型显然的优势
.
深度学习善于从原始输入数据中挖掘越来越抽象的特征表示
,
而这些表示
具有良好的泛化能力
.
它克服了过去人工智能中被认为难以解决的一些问题
.
且随着训练数据集数量的显著增长
以及芯片处理能力的剧增
,
它在目标检测和计算机视觉
、
自然语言处理
、
语音识别和语义分析等领域成效卓然
,
因
此也促进了人工智能的发展
.
深度学习是包含多级非线性变换的层级机器学习方法
,
深层神经网络是目前的主要
形式
,
其神经元间的连接模式受启发于动物视觉皮层组织
,
而卷积神经网络则是其中一种经典而广泛应用的结构
.
卷积神经网络的局部连接
、
权值共享及池化操作等特性使之可以有效地降低网络的复杂度
,
减少训练参数的数目
,
使模型对平移
、
扭曲
、
缩放具有一定程度的不变性
,
并具有强鲁棒性和容错能力
,
且也易于训练和优化
.
基于这些优
越的特性
,
它在各种信号和信息处理任务中的性能优于标准的全连接神经网络
.
该文首先概述了卷积神经网络的
发展历史
,
然后分别描述了神经元模型
、
多层感知器的结构
.
接着
,
详细分析了卷积神经网络的结构
,
包括卷积层
、
池化层
、
全连接层
,
它们发挥着不同的作用
.
然后
,
讨论了网中网模型
、
空间变换网络等改进的卷积神经网络
.
同时
,
还分别介绍了卷积神经网络的监督学习
、
无监督学习训练方法以及一些常用的开源工具
.
此外
,
该文以图像分类
、
人脸识别
、
音频检索
、
心电图分类及目标检测等为例
,
对卷积神经网络的应用作了归纳
.
卷积神经网络与递归神经
网络的集成是一个途径
.
为了给读者以尽可能多的借鉴
,
该文还设计并试验了不同参数及不同深度的卷积神经网
络来分析各参数间的相互关系及不同参数设置对结果的影响
.
最后
,
给出了卷积神经网络及其应用中待解决的若
干问题
.
关键词
卷积神经网络
;
深度学习
;
网络结构
;
训练方法
;
领域数据
中图法分类号
TP18
DOI
号
10.11897
/
SP.J.1016.2017.01229
Review
of
Convolutional
Neural
Network
ZHOU
Fei
-
Yan
1
),
2
)
JIN
Lin
-
Pen
g
1
),
2
)
DONG
Jun
1
)
1
)
(
Suzhou
Institute
o
f
Nano
-
Tech
and
Nano
-
Bionics
,
Chinese
Academ
y
o
f
Sciences
,
Suzhou
,
Jian
g
su
215123
)
2
)
(
Universit
y
o
f
Chinese
Academ
y
o
f
Sciences
,
Bei
j
in
g
100049
)
Abstract
As
a
new
and
ra
p
idl
y
g
rowin
g
field
for
more
than
ten
y
ears
,
dee
p
learnin
g
has
g
ained
more
and
more
attention
from
different
researchers.Com
p
ared
with
shallow
architectures
,
it
has
g
reat
advanta
g
es
in
both
feature
extractin
g
and
model
fittin
g
.And
it
is
ver
y
g
ood
at
discoverin
g
increasin
g
l
y
abstract
feature
re
p
resentations
whose
g
eneralization
abilit
y
is
stron
g
from
the
raw
in
p
ut
data.It
also
has
successfull
y
solved
some
p
roblems
which
were
considered
difficult
to
solve
in
artificial
intelli
g
ence
in
the
p
ast.Furthermore
,
with
the
outstandin
g
l
y
increased
size
of
data
used
for
trainin
g
and
the
drastic
increases
in
chi
p
p
rocessin
g
ca
p
abilities
,
it
has
resulted
in
si
g
nifi
-
cant
p
ro
g
ress
and
been
used
in
a
broad
area
of
a
pp
lications
such
as
ob
j
ect
detection
,
com
p
uter
vision
,
natural
lan
g
ua
g
e
p
rocessin
g
,
s
p
eech
reco
g
nition
and
semantic
p
arsin
g
and
so
on
,
thus
also

p
romotin
g
the
advancement
of
artificial
intelli
g
ence.Dee
p
learnin
g
which
consists
of
multi
p
le
levels
of
non
-
linear
transformations
is
a
hierarchical
machine
learnin
g
method.And
dee
p
neural
network
is
the
main
form
of
the
p
resent
dee
p
learnin
g
method
in
which
the
connectivit
y
p
attern
between
its
neurons
is
ins
p
ired
b
y
the
or
g
anization
of
the
animal
visual
cortex.Convolutional
neural
network
that
has
been
widel
y
used
is
a
classic
kind
of
dee
p
neural
network.There
are
several
characteristics
such
as
local
connections
,
shared
wei
g
hts
,
p
oolin
g
etc.These
features
can
reduce
the
com
p
lexit
y
of
the
network
and
the
number
of
trainin
g
p
arameters
,
and
the
y
also
can
make
the
model
creatin
g
some
de
g
ree
of
invariance
to
shift
,
distortion
and
scale
and
havin
g
stron
g
robustness
and
fault
tolerance.So
it
is
eas
y
to
train
and
o
p
timize
its
network
structure.Based
on
these
p
redominant
characteristics
,
it
has
been
shown
to
out
p
erform
the
standard
full
y
connected
neural
networks
in
a
variet
y
of
si
g
nal
and
information
p
rocessin
g
tasks.In
this
p
a
p
er
,
first
of
all
,
the
historical
develo
p
ment
of
convolutional
neural
network
is
summarized.After
that
,
the
structures
of
a
neuron
model
and
multila
y
er
p
erce
p
tion
are
shown.Later
on
,
a
detailed
anal
y
sis
of
the
convolutional
neural
network
architecture
which
is
com
p
rised
of
a
number
of
convolutional
la
y
ers
and
p
oolin
g
la
y
ers
followed
b
y
full
y
connected
la
y
ers
is
g
iven.Different
kinds
of
la
y
ers
in
convo
-
lutional
neural
network
architecture
p
la
y
different
roles.Then
,
a
few
im
p
roved
al
g
orithms
such
as
Network
in
Network
and
s
p
atial
transformer
networks
of
convolutional
neural
network
are
described.Meanwhile
,
the
su
p
ervised
learnin
g
and
unsu
p
ervised
learnin
g
method
of
convolutional
neural
network
and
some
widel
y
used
o
p
en
source
tools
are
introduced
,
res
p
ectivel
y
.In
addition
,
the
a
pp
lication
of
convolutional
neural
network
on
ima
g
e
classification
,
face
reco
g
nition
,
audio
retrieve
,
electrocardio
g
ram
classification
,
ob
j
ect
detection
,
and
so
on
is
anal
y
zed.Inte
g
ratin
g
of
convolutional
neural
network
and
recurrent
neural
network
to
train
in
p
utted
data
could
be
an
alternative
machine
learnin
g
a
pp
roach.Finall
y
,
different
convolution
neural
network
structures
with
different
p
arameters
and
different
de
p
ths
are
tested.Throu
g
h
a
series
of
ex
p
eriments
,
the
relations
between
these
p
arameters
in
these
models
and
the
influence
of
different
p
arameter
settin
g
s
are
p
reliminar
y
g
ras
p
ed.Some
advanta
g
es
and
remained
issues
of
convolutional
neural
network
and
its
a
pp
lications
are
concluded.
Ke
y
words
convolutional
neural
network
;
dee
p
learnin
g
;
network
structure
;
trainin
g
method
;
domain
data
1
引
言
人工神 经 元 网 络
(
Artificial
Neural
Network
,
ANN
)
是对生物神经网络的一种模拟和近似
,
是由
大量神经元通过相互连接而构成的自适应非线性动
态网络系统
.1943
年
,
心理学家
McCulloch
和数理逻
辑学家
Pitts
提出了神经元的第
1
个数学模型
———
MP
模型
[
1
]
.MP
模型具有开创意义
,
为后来的研究
工作提供了依据
.
到了
20
世纪
50
年代末至
60
年代
初
,
Rosenblatt
在
MP
模型的基础之上增加了学习
功能
,
提出了单层感知器模型
,
第一次把神经网络的
研究付诸实践
[
2
,
3
]
.
但是单层感知器网络模型不能
够处理线 性 不可 分 问 题
.
直 至
1986
年
,
Rumelhart
等人
[
4
]
提出了一种按误差逆传播算法训练的多层前
馈网络
—
反向传播网络
(
Back
Pro
p
a
g
ation
Network
,
BP
网络
),
解决了原来一些单层感知器所不能解决
的问题
.
由于在
20
世纪
90
年代
,
各种浅层机器学习
模型相继被提出
,
较经典的如支持向量机
[
5
]
,
而且当
增加神经网络的层数时传统的
BP
网络会遇到局部
最优
、
过拟合及梯度扩散等问题
,
这些使得深度模型
的研究被搁置
.
2006
年
,
Hinton
等人
[
6
]
在
《
Science
》
上发文
,
其
主要观点有
:(
1
)
多隐层的人工神经网络具有优异
的特征学习能力
;(
2
)
可通 过
“
逐层 预 训练
”(
la
y
er
-
wise
p
re
-
trainin
g
)
来有效克服深层神经网络在训练
上的困难
,
从此引出了深度学习
(
Dee
p
Learnin
g
)
的
研究
,
同时也掀起了人工神经网络的又一热潮
[
7
]
.
在
0321
计
算
机
学
报
2017
年
深度学习的逐层预训练算法中首先将无监督学习应
用于网络每一层的预训练
,
每次只无监督训练一层
,
并将该层的训练结果作为其下一层的输入
,
然后再
用有监督学习
(
BP
算法
)
微调预训练好的网络
[
8
-
10
]
.
这种深度学习预训练方法在手写体数字识别或者行
人检测中
,
特别是当标注样本数量有限时能使识别
效果或者检测效果得到显著提升
[
11
]
.Ben
g
io
[
12
]
系统
地介绍了深度学习所包含的网络结构和学习方法
.
目前
,
常用的深度学习模型有深度置信网络
(
Dee
p
Belief
Network
,
DBN
)
[
13
-
16
]
、
层 叠 自 动 去 噪 编 码 机
(
Stacked
Deoisin
g
Autoencoders
,
SDA
)
[
17
,
18
]
、
卷积神
经网络
(
Convolutional
Neural
Network
,
CNN
)
[
19
,
20
]
等
.2016
年
1
月
28
日
,
英国
《
Nature
》
杂志以封面文章
形式报道
:
谷歌旗下人工智能公司深灵
(
Dee
p
Mind
)
开发的
Al
p
haGo
以
5∶0
战胜了卫冕欧洲冠军
———
本以为大概
10
年后人工智能才能做到
[
21
]
.Al
p
haGo
主要采用价值网络
(
value
networks
)
来评估棋盘的
位置
,
用策略网络
(
p
olic
y
networks
)
来选择下棋步
法
,
这两种网络都是深层神经网络模型
,
Al
p
haGo
所取得的成果是深度学习带来的人工智能的又一次
突破
,
这也说明了深度学习具有强大的潜力
.
事实上
,
早在
2006
年以前就已有人提出一种学
习效率很高 的深度 学习模 型
———
CNN.
在
20
世纪
80
年代和
90
年代
,
一些研究者发表了
CNN
的相关
研究工作
,
且在几个模式识别领域尤其是手写数字识
别中取得了良好的识别效果
[
22
,
23
]
.
然而此时的
CNN
只适合做小图片 的 识别
,
对于 大 规模 数 据
,
识别 效
果不佳
[
7
]
.
直至
2012
年
,
Krizhevsk
y
等人
[
24
]
使用扩
展了深度的
CNN
在
Ima
g
eNet
大规模视觉识别挑
战竞赛
(
Ima
g
eNet
Lar
g
e
Scale
Visual
Reco
g
nition
Challen
g
e
,
LSVRC
)
中取得了当时最佳的分类效果
,
使得
CNN
越来越受研究者们的重视
.
2
CNN
概述
2.1
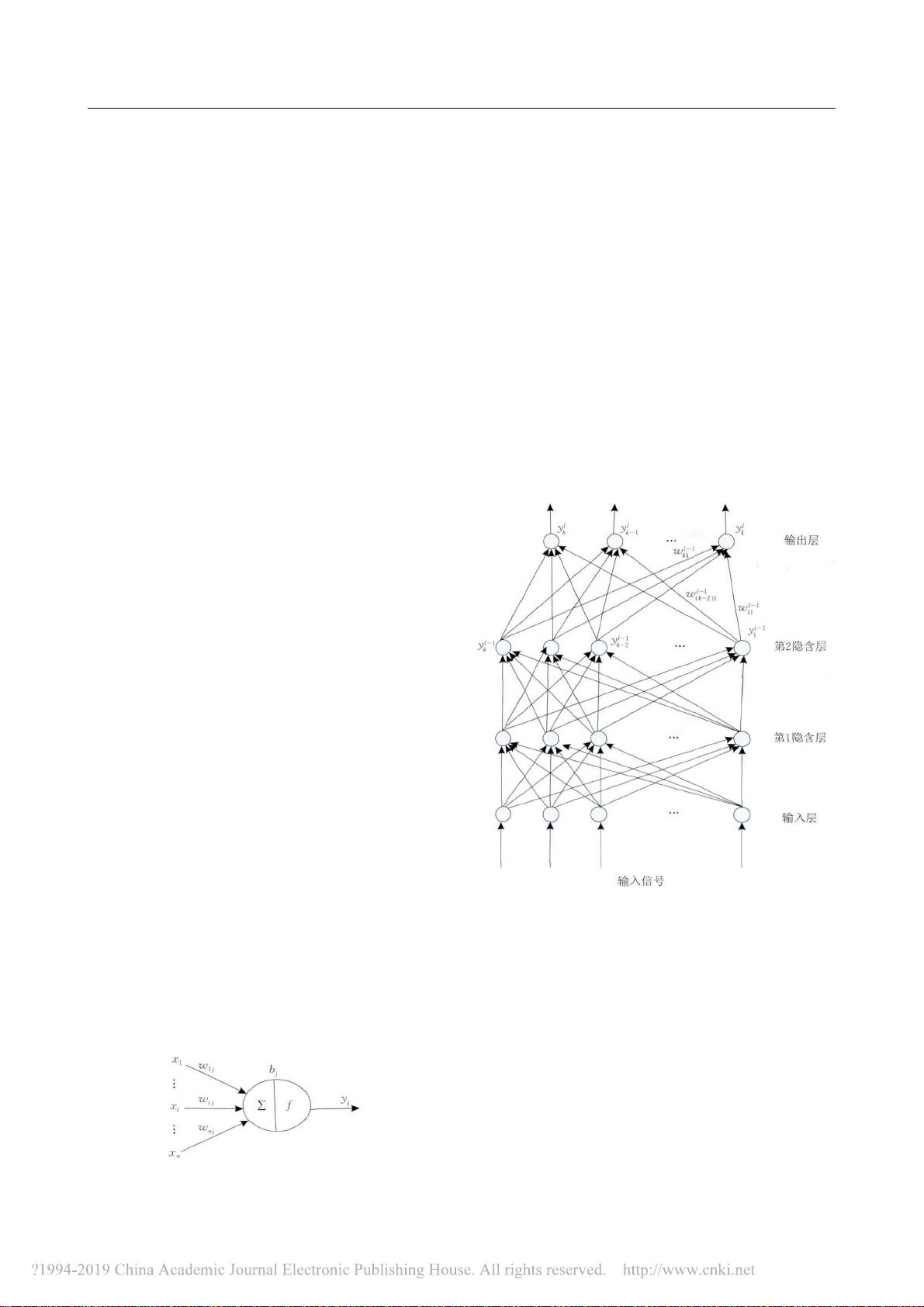
神经元
神经元是人工神经网络的基本处理单元
,
一般
是多输入单输出的单元
,
其结构模型如图
1
所示
.
图
1
神经元模型
其中
:
x
i
表示输入信号
;
n
个输入信号同时输入神经
元
j
.
w
i
j
表示输入信号
x
i
与神经元
j
连接的权重值
,
b
j
表示神经元的内部状态即偏置值
,
y
j
为神经元的
输出
.
输入与输出之间的对应关系可用下式表示
:
y
j
=
f
b
j
+
∑
n
i
=
1
(
x
i
×
w
i
j
( )
) (
1
)
f
(·)
为激励函数
,
其可以有很多种选 择
,
可以是线
性 纠 正 函 数
(
Rectified
Linear
Unit
,
ReLU
)
[
25
]
,
si
g
moid
函数
、
tanh
(
x
)
函数
、
径向基函数等
[
26
]
.
2.2
多层感知器
多层 感 知 器
(
Multila
y
er
Perce
p
tron
,
MLP
)
是
由输入层
、
隐含层
(
一层或者多层
)
及输出层构成的
神经网络模型
,
它可以解决单层感知器不能解决的
线性不可分问题
.
图
2
是含有
2
个隐含层的多层感
知器网络拓扑结构图
.
图
2
多层感知器结构图
输入层神经元接收输入信号
,
隐含层和输出层
的每一个神经元与之相邻层的所有神经元连接
,
即
全连接
,
同一层的神经元间不相连
.
图
2
中
,
有箭头
的线段表示神经元间的连接和信号传输的方向
,
且
每个连接都有一个连接权值
.
隐含层和输出层中每
一个神经元的输入为前一层所有神经元输出值的加
权和
.
假设
x
l
m
是
MLP
中第
l
层第
m
个神经元的输
入值
,
y
l
m
和
b
l
m
分别为该神经元输出值和偏置值
,
w
l
-1
im
为该神经元与第
l
-1
层第
i
个神经元的连接
权值
,
则有
:
1321
6
期 周飞燕等
:
卷积神经网络研究综述

x
l
m
=
b
l
m
+
∑
k
i
=
1
w
l
-
1
im
×
y
l
-
1
i
(
2
)
y
l
m
=
f
(
x
l
m
) (
3
)
当多层感知器用于分类时
,
其输入神经元个数
为输入信号的维数
,
输出神经元个数为类别数
,
隐含
层个数及隐层神经元个数视具体情况而定
.
但在实
际应用中
,
由于受到参数学习效率影响
,
一般使用不
超过
3
层的浅层模型
.BP
算法可分为两个阶段
:
前
向传播和后 向 传 播
,
其后向传播始于
MLP
的输出
层
.
以图
2
为例
,
则损失函数为
[
27
]
E
=
E
(
y
l
1
,…,
y
l
h
)
=
∑
h
j
(
y
l
j
-
t
j
)
2
(
4
)
其中第
l
层为输出层
,
t
j
为输出层第
j
个神经元的期
望输出
,
对损失函数求一阶偏导
,
则网络权值更新公
式为
w
l
-
1
im
=
w
l
-
1
im
-
η
×
E
w
l
-
1
im
(
5
)
其中
,
η
为学习率
.
2.3
CNN
1962
年
,
生物 学 家
Hubel
和
Wiesel
[
28
]
通过 对
猫脑视觉皮层的研究
,
发现在视觉皮层中存在一系
列复杂构造的细胞
,
这些细胞对视觉输入空间的局
部区域很敏感
,
它们被称为
“
感受野
”
.
感受野以某种
方式覆盖整个视觉域
,
它在输入空间中起局部作用
,
因而能够更好地挖掘出存在于自然图像中强烈的局
部空间相关性
.
文献
[
28
]
将这些被称为感受野的细
胞分为简单细胞和复杂细胞两种类型
.
根据
Hubel
-
Wiesel
的层级模型
,
在视觉皮层中的神经网络有一
个层级结构
:
外侧膝状体
→
简单细胞
→
复杂细胞
→
低阶超复杂细胞
→
高阶超复杂细胞
[
29
]
.
低阶超复杂
细胞与高阶超复杂细胞之间的神经网络结构类似于
简单细胞和复杂细胞间的神经网络结构
.
在该层级
结构中
,
处于较高阶段的细胞通常会有这样一个倾
向
:
选择性地响应刺激模式更复杂的特征
;
同时还具
有一个更大的感受野
,
对刺激模式位置的变化更加
不敏感
[
29
]
.1980
年
,
Fukushima
根据
Huble
和
Wiesel
的层级模型提出了结构与之类似的神经认知机
(
Neoco
g
nitron
)
[
29
]
.
神经认知机采用简单细胞层
(
S
-
la
y
er
,
S
层
)
和复杂细胞层
(
C
-
la
y
er
,
C
层
)
交替组
成
,
其中
S
层与
Huble
-
Wiesel
层级模型中的简单细
胞层或者低阶超复杂细胞层相对应
,
C
层对应于复
杂细胞层或者高阶超复杂细胞层
.S
层能够最大程度
地响应感受野内的特定边缘刺激
,
提取其输入层的
局部特征
,
C
层对来自确切位置的刺激具有局部不
敏感性
.
尽管在神经认知机中没有像
BP
算法那样
的全局监督学习过程可利用
,
但它仍可认为是
CNN
的第一个工程实现网络
,
卷积和池 化
(
也称 作 下采
样
)
分别受启发于
Hubel
-
Wiesel
概念的简单细胞和
复杂细胞
,
它能够准确识别具有位移和轻微形变的
输入 模 式
[
29
,
30
]
.
随 后
,
LeCun
等 人 基 于
Fukushima
的研究工作使用
BP
算法设计并训练了
CNN
(
该模
型称为
LeNet
-
5
),
LeNet
-
5
是经典的
CNN
结构
,
后
续有许多工作基于此进行改进
,
它在一些模式识别
领域中取得了良好的分类效果
[
19
]
.
CNN
的基本结构由输入层
、
卷 积 层
(
convolu
-
tional
la
y
er
)、
池 化 层
(
p
oolin
g
la
y
er
,
也 称 为 取 样
层
)、
全连接层及输出层构成
.
卷积层和池化层一般会
取若干个
,
采用卷积层和池化层交替设置
,
即一个卷
积层连接一个池化层
,
池化层后再连接一个卷积层
,
依此类推
.
由于卷积层中输出特征面的每个神经元与
其输入进行局部连接
,
并通过对应的连接权值与局部
输入进行加权求和再加上偏置值
,
得到该神经元输入
值
,
该过程等同于卷积过程
,
CNN
也由此而得名
[
19
]
.
2.3.1
卷积层
卷积层由多个特征面
(
Feature
Ma
p
)
组成
,
每个
特征面由多个神经元组成
,
它的每一个神经元通过
卷积核与上一层特征面的局部区域相连
.
卷积核是
一个权值矩阵
(
如对于二维图像而言可为
3×3
或
5×5
矩阵
)
[
19
,
31
]
.CNN
的卷积层通过卷积操作提取
输入的不同特征
,
第
1
层卷积层提取低级特征如边
缘
、
线条
、
角落
,
更高层的卷积层提取更高级的特征
①
.
为了能够更 好 地理解
CNN
,
下面 以 一维
CNN
(
1D
CNN
)
为 例
,
二 维 和 三 维
CNN
可 依 此 进 行 拓 展
.
图
3
所示为一维
CNN
的卷积层和池化层结构示意
图
,
最顶层为池化层
,
中间层为卷积层
,
最底层为卷
积层的输入层
.
由图
3
可看出卷积层的神经元被组织到各个特
征面中
,
每个神经元通过一组权值被连接到上一层
特征面的局部区域
,
即卷积层中的神经元与其输入
层中的特征面进行局部连接
[
11
]
.
然后将该局部加权
和传递给一个非线性函数如
ReLU
函数 即 可获 得
卷积层中每个神经元的输出值
.
在同一个输入特征
面和同一个输出特征面中
,
CNN
的 权 值 共 享
,
如
图
3
所示
,
权值共享发生在同一种颜色当中
,
不同颜色
权值不共享
.
通过权值共享可以减小模型复杂度
,
使
2321
计
算
机
学
报
2017
年
①
Hi
j
azi
S
,
Kumar
R
,
Rowen
C
,
et
al.Usin
g
convolutional
neural
networks
for
ima
g
e
reco
g
nition.htt
p
://
i
p
.cadence.
com
/
u
p
loads
/
901
/
cnn
_
w
p
-
p
df
,
2016
,
9
,
22
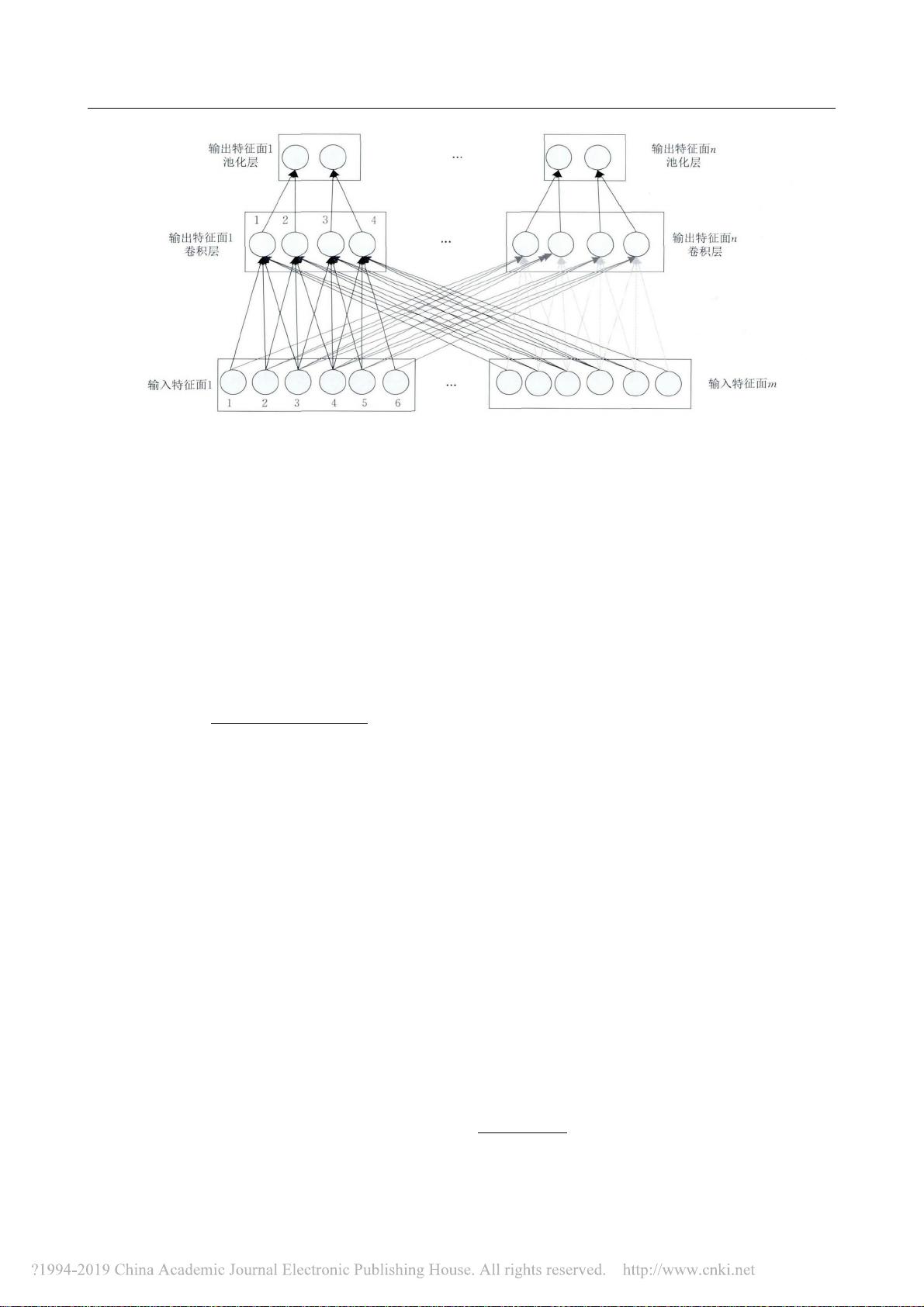
图
3
卷积层与池化层结构示意图
得网络更 易 于 训 练
.
以 图
3
中 卷 积 层 的 输 出 特 征
面
1
和其输 入 层 的 输 入 特 征 面
1
为 例
,
w
1
(
1
)
1
(
1
)
=
w
1
(
2
)
1
(
2
)
=
w
1
(
3
)
1
(
3
)
=
w
1
(
4
)
1
(
4
)
,
而
w
1
(
1
)
1
(
1
)
≠
w
1
(
2
)
1
(
1
)
≠
w
1
(
3
)
1
(
1
)
,
其中
w
m
(
i
)
n
(
j
)
表示输入特征面
m
第
i
个神经
元与输出特征面
n
第
j
个神经元的连接权值
.
此外
卷积核的滑动步长即卷积核每一次平移的距离也是
卷积层中一个重要的参数
.
在图
3
中
,
设置卷积核在
上一层的滑动步长为
1
,
卷积核大小为
1×3.CNN
中每一个卷积层的每个输出特征面的大小
(
即神经
元的个数
)
oMa
p
N
满足如下关系
[
32
]
oMa
p
N
=
(
iMa
p
N
-
CWindow
)
CInterval
( )
+1
(
6
)
其 中
:
iMa
p
N
表 示 每 一 个 输 入 特 征 面 的 大 小
;
CWindow
为卷积核的大小
;
CInterval
表示卷积核
在其上一层的滑动步长
.
通常情况下
,
要保证式
(
6
)
能够整除
,
否则需对
CNN
网络结构作额外处理
.
每
个卷积层可训练参数数目
CParams
满足式
(
7
)
[
32
]
CParams
=
(
iMa
p
×
CWindow
+1
)
×
oMa
p
(
7
)
其中
:
oMa
p
为 每 个 卷 积 层 输 出 特 征 面 的 个 数
;
iMa
p
为输入特征面个数
.1
表示偏置
,
在同一个输
出特征面中偏置也共享
.
假设卷积层中输出特征面
n
第
k
个神经元的输出值为
x
out
nk
,
而
x
in
mh
表示其输入
特征面
m
第
h
个 神 经 元 的 输 出 值
,
以 图
3
为 例
,
则
[
32
]
x
out
nk
=
f
cov
(
x
in
1
h
×
w
1
(
h
)
n
(
k
)
+
x
in
1
(
h
+
1
)
×
w
1
(
h
+
1
)
n
(
k
)
+
x
in
1
(
h
+
2
)
×
w
1
(
h
+
2
)
n
(
k
)
+
…
+
b
n
) (
8
)
式
(
8
)
中
,
b
n
为输出特征面
n
的偏置值
.
f
cov
(·)
为非
线性激 励函 数
.
在 传 统 的
CNN
中
,
激 励 函 数 一 般
使用饱 和 非 线 性 函 数
(
saturatin
g
nonlinearit
y
)
如
si
g
moid
函数
、
tanh
函数等
.
相比较于饱和非线性函
数
,
不饱和非线性函数
(
non
-
saturatin
g
nonlinearit
y
)
能够解决梯度爆炸
/
梯度消失问题
,
同时也能够加快
收敛速度
[
33
]
.Jarrett
等人
[
34
]
探讨了卷积网络中不
同的纠正非线性函数
(
rectified
nonlinearit
y
,
包 括
max
(
0
,
x
)
非线性函数
),
通过实验发现它们能够显
著提升卷积网络的性能
,
Nair
等人
[
25
]
也验证了这一
结论
.
因此在目前的
CNN
结构中常用不饱和非线性
函数作为卷积层的激励函数如
ReLU
函数
.ReLU
函
数的计算公式如下所示
[
24
,
25
]
f
cov
(
x
)
=
max
(
0
,
x
) (
9
)
图
4
中实线为
ReLU
曲线
,
虚线为
tanh
曲线
.
对于
ReLU
而言
,
如果输入大于
0
,
则输出与输入相
等
,
否则输出为
0.
从图
4
可以看出
,
使用
ReLU
函
数
,
输出不会随着输入的逐渐增加而趋于饱和
.
Chen
在其报告中分析 了 影响
CNN
性能 的
3
个因
素
:
层数
、
特征面的数目及网络组织
①
.
该报告使用
9
种结构的
CNN
进行中文手写体识别实验
,
通过统
计测试结果得到具有较小卷积核的
CNN
结构的一
些结 论
:(
1
)
增加网络的深度能够提升准确率
;
(
2
)
增加特征面的数目也可以提升准确率
;(
3
)
增加
一个卷积层比增加一个全连接层更能获得一个更高
的准确率
.Ben
g
io
等人
[
35
]
指出深度网络结构具有两
个优点
:(
1
)
可以促进特征的重复利用
;(
2
)
能够获取
高层表达中更抽象的特征
,
由于更抽象的概念可根
据抽象性更弱的概念来构造
,
因此深度结构能够获
取更抽象的表达
,
例如在
CNN
中通过池化操作来
3321
6
期 周飞燕等
:
卷积神经网络研究综述
①
Xu
Chen.Convolution
neural
networks
for
Chinese
hand
-
writin
g
reco
g
nition.htt
p
://
cs231n.stanford.edu
/
re
p
orts2016
/
428
_
Re
p
ort.
p
df
,
2016
,
9
,
22
剩余22页未读,继续阅读
olivia_ye
- 粉丝: 10
- 资源: 85
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
- SPC统计方法基础知识.pptx
- MW全能培训汽轮机调节保安系统PPT教学课件.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0