没有合适的资源?快使用搜索试试~ 我知道了~
首页Probabilistic Inference Using Markov Chain Monte Carlo Methods
Probabilistic Inference Using Markov Chain Monte Carlo Methods
Probabilistic Inference Using Markov Chain Monte Carlo Methods
资源详情
资源评论
资源推荐

Probabilistic Inference Using
Markov Chain Monte Carlo Metho ds
Radford M. Neal
Technical Report CRG-TR-93-1
Department of Computer Science
UniversityofToronto
E-mail: radford@cs.toronto.edu
25 September 1993
c
Copyright 1993 by Radford M. Neal

Abstract
Probabilistic inference is an attractive approach to uncertain reasoning and em-
pirical learning in articial intelligence. Computational diculties arise, however,
because probabilistic models with the necessary realism and exibility lead to com-
plex distributions over high-dimensional spaces.
Related problems in other elds have been tackled using Monte Carlo metho ds based
on sampling using Markovchains, providing a rich arrayoftechniques that can b e
applied to problems in articial intelligence. The \Metropolis algorithm" has been
used to solve dicult problems in statistical physics for over fortyyears, and, in the
last few years, the related metho d of \Gibbs sampling" has b een applied to problems
of statistical inference. Concurrently, an alternative method for solving problems
in statistical physics by means of dynamical simulation has been developed as well,
and has recently been unied with the Metrop olis algorithm to produce the \hybrid
Monte Carlo" method. In computer science, Markovchain sampling is the basis
of the heuristic optimization technique of \simulated annealing", and has recently
been used in randomized algorithms for approximate counting of large sets.
In this review, I outline the role of probabilistic inference in articial intelligence,
present the theory of Markovchains, and describ e various Markovchain Monte
Carlo algorithms, along with a number of supporting techniques. I try to presenta
comprehensive picture of the range of methods that have been developed, including
techniques from the varied literature that have not yet seen wide application in
articial intelligence, but which app ear relevant. As illustrative examples, I use the
problems of probabilistic inference in exp ert systems, discovery of latent classes from
data, and Bayesian learning for neural networks.
Acknowledgements
I thank David MacKay, Richard Mann, Chris Williams, and the members of my
Ph.D committee, Georey Hinton, Rudi Mathon, Demetri Terzop oulos, and Rob
Tibshirani, for their helpful comments on this review. This work was supp orted
by the Natural Sciences and Engineering Research Council of Canada and by the
Ontario Information Technology Research Centre.

Contents
1.Intro duction 1
2. Probabilistic Inference for Articial Intelligence 4
2.1 Probabilistic inference with a fully-sp ecied model
::::: ::::::::::
5
2.2 Statistical inference for mo del parameters
::::::: :::::::::: :::
13
2.3 Bayesian mo del comparison
:::: ::::::::::: :::::::::: :::
23
2.4 Statistical physics
::::::: :::::::::: ::::::::::: ::::::
25
3. Background on the Problem and its Solution 30
3.1 Denition of the problem
::::: ::::::::::: :::::::::: :::
30
3.2 Approaches to solving the problem
::::::: ::::::::::: ::::::
32
3.3 Theory of Markovchains
:::::: ::::::::::: :::::::::: :::
36
4. The Metropolis and Gibbs Sampling Algorithms 47
4.1 Gibbs sampling
:::: ::::::::::: :::::::::: ::::::::::
47
4.2 The Metrop olis algorithm
::::: ::::::::::: :::::::::: :::
54
4.3 Variations on the Metrop olis algorithm
::::: ::::::::::: ::::::
59
4.4 Analysis of the Metropolis and Gibbs sampling algorithms
::::: ::::::
64
5. The Dynamical and Hybrid Monte Carlo Metho ds 70
5.1 The sto chastic dynamics metho d
::::: :::::::::: ::::::::::
70
5.2 The hybrid Monte Carlo algorithm
::::::: ::::::::::: ::::::
77
5.3 Other dynamical metho ds
::::: ::::::::::: :::::::::: :::
81
5.4 Analysis of the hybrid Monte Carlo algorithm
::::: :::::::::: :::
83
6. Extensions and Renements 87
6.1 Simulated annealing
::::: :::::::::: ::::::::::: ::::::
87
6.2 Free energy estimation
::::::: ::::::::::: :::::::::: :::
94
6.3 Error assessment and reduction
:::::: :::::::::: ::::::::::
102
6.4 Parallel implementation
:::::: ::::::::::: :::::::::: :::
114
7. Directions for Research 116
7.1 Improvements in the algorithms
:::::: :::::::::: ::::::::::
116
7.2 Scope for applications
::::::: ::::::::::: :::::::::: :::
118
8. Annotated Bibliography 121
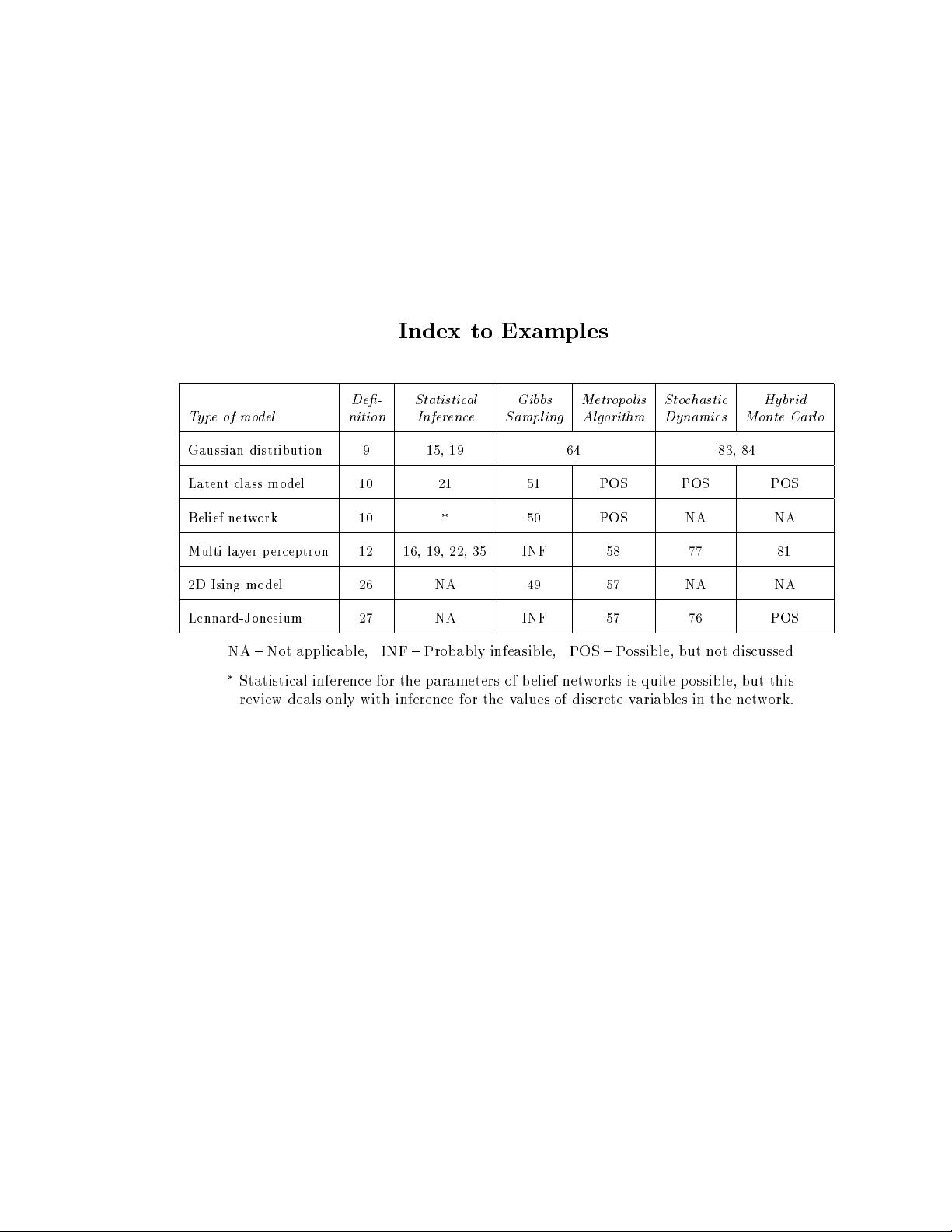
Index to Examples
De- Statistical Gibbs Metropolis Stochastic Hybrid
Typeofmodel nition Inference Sampling Algorithm Dynamics Monte Carlo
Gaussian distribution 9 15, 19 64 83, 84
Latent class mo del 10 21 51 POS POS POS
Belief network 10 * 50 POS NA NA
Multi-layer p erceptron 12 16, 19, 22, 35 INF 58 77 81
2D Ising model 26 NA 49 57 NA NA
Lennard-Jonesium 27 NA INF 57 76 POS
NA { Not applicable, INF { Probably infeasible, POS { Possible, but not discussed
Statistical inference for the parameters of b elief networks is quite p ossible, but this
review deals only with inference for the values of discrete variables in the network.

1. Intro duction
Probabilityisawell-understo od method of representing uncertain knowledge and reasoning
to uncertain conclusions. It is applicable to low-level tasks such as p erception, and to high-
level tasks such as planning. In the Bayesian framework, learning the probabilistic models
needed for such tasks from empirical data is also considered a problem of probabilistic in-
ference, in a larger space that encompasses various possible models and their parameter
values. To tackle the complex problems that arise in articial intelligence, exible meth-
ods for formulating mo dels are needed. Techniques that have been found useful include
the sp ecication of dep endencies using \b elief networks", approximation of functions using
\neural networks", the introduction of unobservable \latentvariables", and the hierarchical
formulation of models using \hyperparameters".
Such exible mo dels come with a price however. The probability distributions they give rise
to can b e very complex, with probabilities varying greatly over a high-dimensional space.
There maybenoway to usefully characterize such distributions analytically. Often, however,
a sample of p oints drawn from such a distribution can provide a satisfactory picture of it.
In particular, from such a sample we can obtain
Monte Carlo
estimates for the expectations
of various functions of the variables. Suppose
X
=
f
X
1
;
...
;X
n
g
is the set of random
variables that characterize the situation b eing mo deled, taking on values usually written as
x
1
;
...
;x
n
, or some typographical variation thereon. These variables might, for example,
represent parameters of the model, hidden features of the ob jects mo deled, or features of
ob jects that may b e observed in the future. The expectation of a function
a
(
X
1
;
...
;X
n
)
| it's average value with respect to the distribution over
X
| can b e approximated by
h
a
i
=
X
~
x
1
X
~
x
n
a
(~
x
1
;
...
;
~
x
n
)
P
(
X
1
=~
x
1
;
...
;X
n
=~
x
n
) (1.1)
1
N
N
1
X
t
=0
a
(
x
(
t
)
1
;
...
;x
(
t
)
n
) (1.2)
where
x
(
t
)
1
;
...
;x
(
t
)
n
are the values for the
t
-th point in a sample of size
N
. (As ab ove, I will
often distinguish variables in summations using tildes.) Problems of prediction and decision
can generally be formulated in terms of nding such expectations.
Generating samples from the complex distributions encountered in articial intelligence
applications is often not easy,however. Typically, most of the probability is concentrated
in regions whose volume is a tiny fraction of the total. To generate points drawn from
the distribution with reasonable eciency, the sampling procedure must search for these
relevant regions. It must do so, moreover, in a fashion that does not bias the results.
Sampling metho ds based on
Markov chains
incorporate the required search aspect in a
framework where it can be proved that the correct distribution is generated, at least in
the limit as the length of the chain grows. Writing
X
(
t
)
=
f
X
(
t
)
1
;
...
;X
(
t
)
n
g
for the set of
variables at step
t
, the chain is dened by giving an initial distribution for
X
(0)
and the
transition probabilities for
X
(
t
)
given the value for
X
(
t
1)
. These probabilities are chosen
so that the distribution of
X
(
t
)
converges to that for
X
as
t
increases, and so that the
Markovchain can feasibly b e simulated by sampling from the initial distribution and then,
in succession, from the conditional transition distributions. For a suciently long chain,
equation (1.2) can then b e used to estimate exp ectations.
1
剩余143页未读,继续阅读
sjxhill
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- 2023年中国辣条食品行业创新及消费需求洞察报告.pptx
- 2023年半导体行业20强品牌.pptx
- 2023年全球电力行业评论.pptx
- 2023年全球网络安全现状-劳动力资源和网络运营的全球发展新态势.pptx
- 毕业设计-基于单片机的液体密度检测系统设计.doc
- 家用清扫机器人设计.doc
- 基于VB+数据库SQL的教师信息管理系统设计与实现 计算机专业设计范文模板参考资料.pdf
- 官塘驿林场林防火(资源监管)“空天地人”四位一体监测系统方案.doc
- 基于专利语义表征的技术预见方法及其应用.docx
- 浅谈电子商务的现状及发展趋势学习总结.doc
- 基于单片机的智能仓库温湿度控制系统 (2).pdf
- 基于SSM框架知识产权管理系统 (2).pdf
- 9年终工作总结新年计划PPT模板.pptx
- Hytera海能达CH04L01 说明书.pdf
- 数据中心运维操作标准及流程.pdf
- 报告模板 -成本分析与报告培训之三.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论2