没有合适的资源?快使用搜索试试~ 我知道了~
首页粒子群算法详解 附详细实现代码
粒子群算法入门必备,超详细。 在全局版的标准粒子群算法中,每个粒子的速度的更新是根据两个因素来变化的,这两个因素是:1. 粒子自己历史最优值pi。2. 粒子群体的全局最优值pg。如果改变粒子速度更新公式,让每个粒子的速度的更新根据以下两个因素更新,A. 粒子自己历史最优值pi。B. 粒子邻域内粒子的最优值pnk。其余保持跟全局版的标准粒子群算法一样,这个算法就变为局部版的粒子群算法。
资源详情
资源评论
资源推荐
粒子群算法(1)----粒子群算法简介
一、粒子群算法的历史
粒子群算法源于复杂适应系统(Complex Adaptive System,CAS)。CAS 理论于 1994 年正式提出,CAS 中的
成员称为主体。比如研究鸟群系统,每个鸟在这个系统中就称为主体。主体有适应性,它能够与环境及其他的主体进
行交流,并且根据交流的过程“学习”或“积累经验”改变自身结构与行为。整个系统的演变或进化包括:新层次的产生
(小鸟的出生);分化和多样性的出现(鸟群中的鸟分成许多小的群);新的主题的出现(鸟寻找食物过程中,不断
发现新的食物)。
所以 CAS 系统中的主体具有 4 个基本特点(这些特点是粒子群算法发展变化的依据):
首先,主体是主动的、活动的。
主体与环境及其他主体是相互影响、相互作用的,这种影响是系统发展变化的主要动力。
环境的影响是宏观的,主体之间的影响是微观的,宏观与微观要有机结合。
最后,整个系统可能还要受一些随机因素的影响。
粒子群算法就是对一个 CAS 系统---鸟群社会系统的研究得出的。
粒子群算法( Particle Swarm Optimization, PSO)最早是由 Eberhart 和 Kennedy 于 1995 年提出,它的基本概
念源于对鸟群觅食行为的研究。设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都
不知道食物在哪里,但是它们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢?最简单有效的就
是搜寻目前离食物最近的鸟的周围区域。
PSO 算法就从这种生物种群行为特性中得到启发并用于求解优化问题。在 PSO 中,每个优化问题的潜在解都可
以想象成 d 维搜索空间上的一个点,我们称之为“粒子”(Particle),所有的粒子都有一个被目标函数决定的适应值
(Fitness Value ),每个粒子还有一个速度决定他们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中
搜索。Reynolds 对鸟群飞行的研究发现。鸟仅仅是追踪它有限数量的邻居但最终的整体结果是整个鸟群好像在一个
中心的控制之下.即复杂的全局行为是由简单规则的相互作用引起的。
二、粒子群算法的具体表述
上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO 的历史就像上面说的那样。下面通俗的解释
PSO 算法。
PSO 算法就是模拟一群鸟寻找食物的过程,每个鸟就是 PSO 中的粒子,也就是我们需要求解问题的可能解,这
些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。大家也可以观察一下,鸟群在寻找食物的过程中,
开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。这个过程我们转化
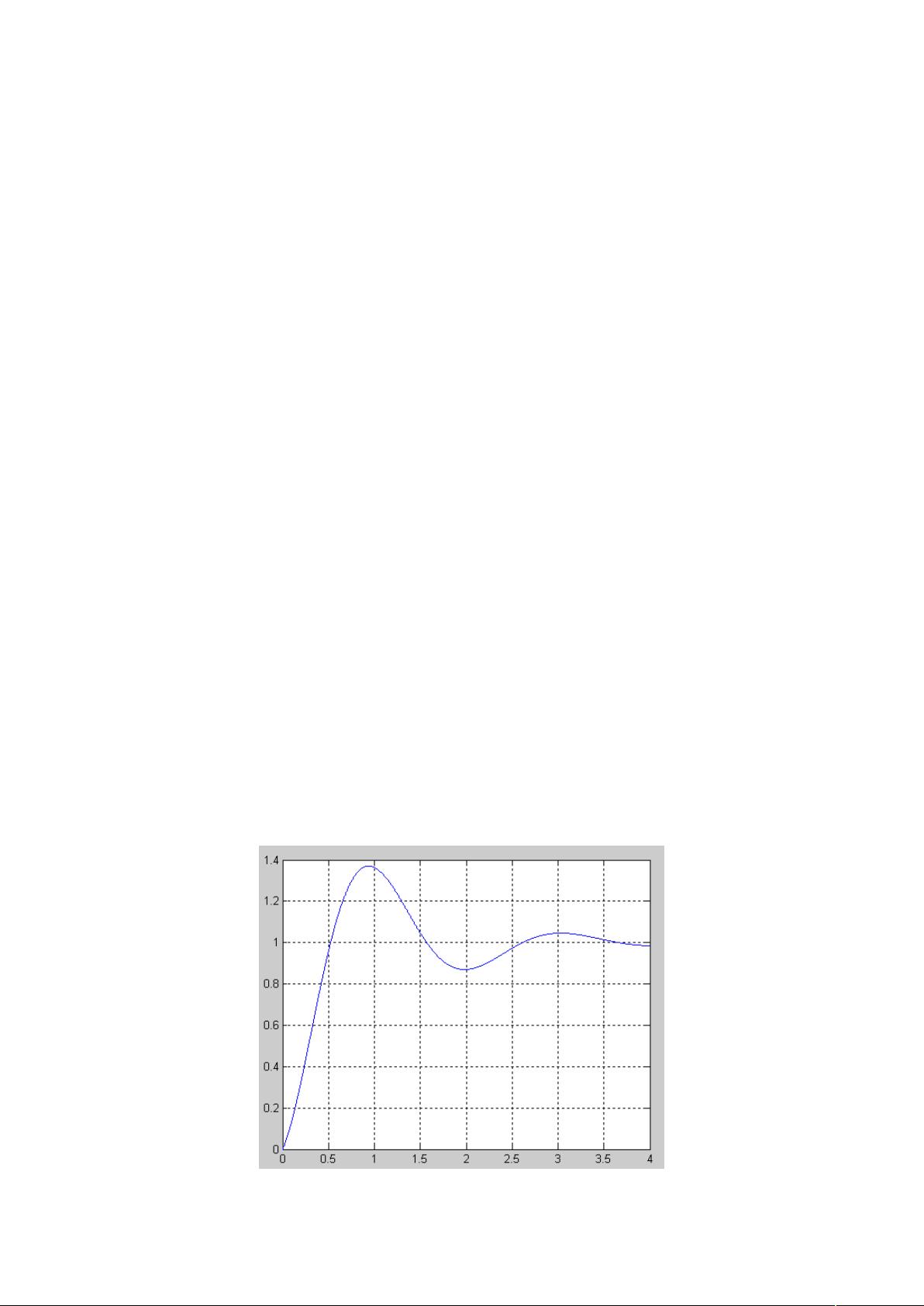
为一个数学问题。寻找函数 y=1-cos(3*x)*exp(-x)的在[0,4]最大值。该函数的图形如下:
当 x=0.9350-0.9450,达到最大值 y=1.3706。为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为
了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。下面这些点
就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在 y=1.3706 这个点停止自己的更新。这个过程与粒子群算法作为对照如下:
这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物
计算两个点函数值就是粒子群算法中的适应值,计算用的函数 y=1-cos(3*x)*exp(-x)就是粒子群算法中的适应度
函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式(下一节讲)。
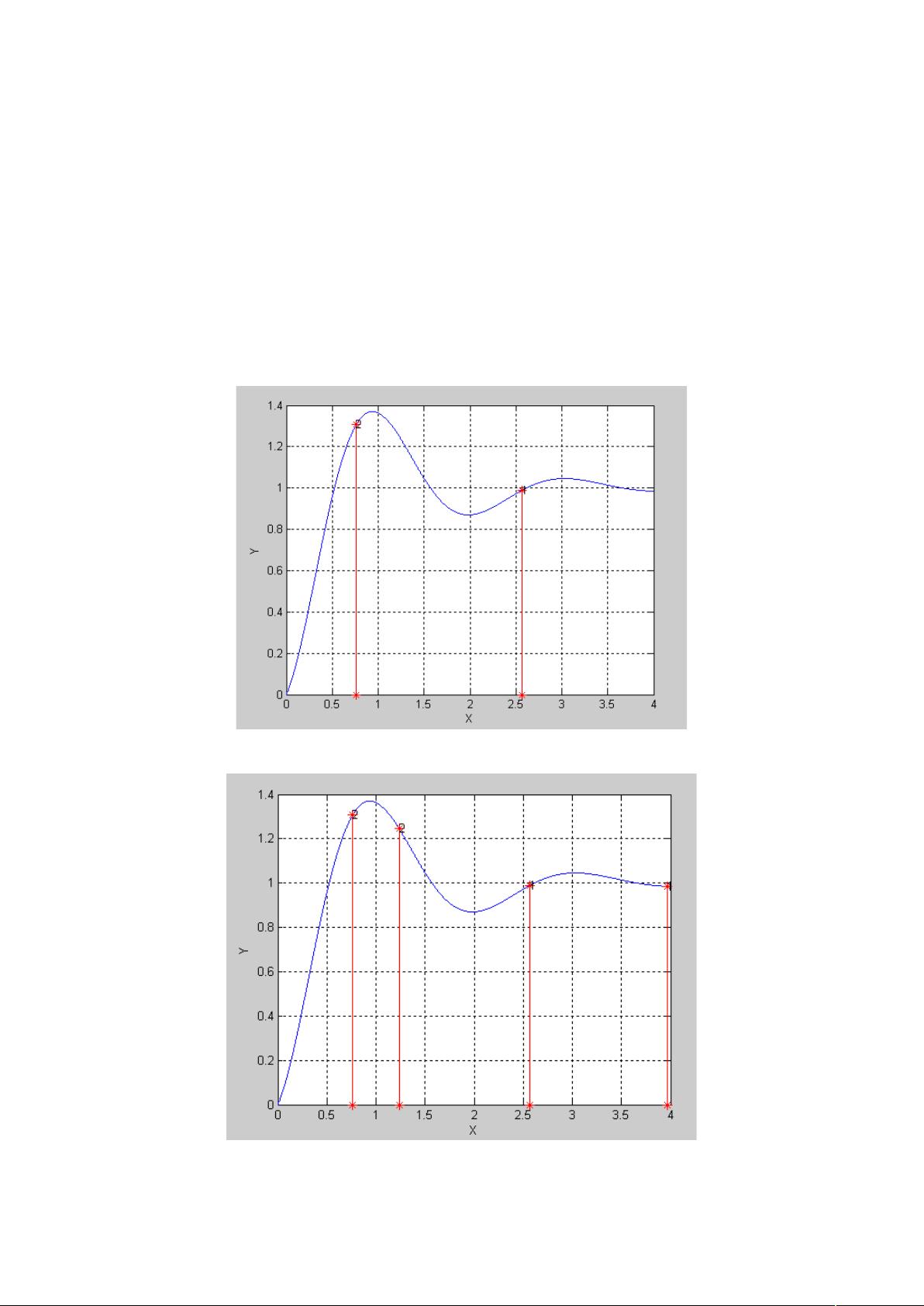
下面演示一下这个算法运行一次的大概过程:
第一次初始化
第一次更新位置
第二次更新位置

第 21 次更新
最后的结果(30 次迭代)
最后所有的点都集中在最大值的地方。

粒子群算法(2)----标准的粒子群算法
在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式
更新。这个公式就是粒子群算法中的位置速度更新公式。下面就介绍这个公式是什么。在上一节中我们求取函数 y=1-
cos(3*x)*exp(-x)的在[0,4]最大值。并在[0,4]之间放置了两个随机的点,这些点的坐标假设为 x1=1.5; x2=2.5;这里
的点是一个标量,但是我们经常遇到的问题可能是更一般的情况--x 为一个矢量的情况,比如二维的情况
z=2*x1+3*x2
2
的情况。这个时候我们的每个粒子为二维,记粒子 P1=
(x11,x12),P2=(x21,x22),P3=(x31,x32),......Pn=(xn1,xn2)。这里 n 为粒子群群体的规模,也就是这个群中粒子的个数,
每个粒子的维数为 2。更一般的是粒子的维数为 q,这样在这个种群中有 n 个粒子,每个粒子为 q 维。
由 n 个粒子组成的群体对 Q 维(就是每个粒子的维数)空间进行搜索。每个粒子表示为:x
i
=
(x
i1
,x
i2
,x
i3
,...,x
iQ
),每个粒子对应的速度可以表示为 v
i
=(v
i1
,v
i2
,v
i3
,....,v
iQ
),每个粒子在搜索时要考虑两个因素:
1。自己搜索到的历史最优值 p
i
,
p
i
=(p
i1
,p
i2
,....,p
iQ
),i=1,2,3,....,n。
2。全部粒子搜索到的最优值 p
g
,
p
g
=(p
g1
,p
g2
,....,p
gQ
),注意这里的 p
g
只有一个。
下面给出粒子群算法的位置速度更新公式:
这里有几个重要的参数需要大家记忆,因为在以后的讲解中将会经常用到:
它们是:
是保持原来速度的系数,所以叫做惯性权重。
是粒子跟踪自己历史最优值的权重系数,它表示粒子自身的认识,所以叫“认知”。通常设置为 2。
是粒子跟踪群体最优值的权重系数,它表示粒子对整个群体知识的认识,所以叫做“社会知识”,经常叫做“社会”。
通常设置为 2。
是[0,1]区间内均匀分布的随机数。
是对位置更新的时候,在速度前面加的一个系数,这个系数我们叫做约束因子。通常设置为 1。
这样一个标准的粒子群算法就结束了。
下面对整个基本的粒子群的过程给一个简单的图形表示:

判断终止条件可是设置适应值到达一定的数值或者循环一定的次数。
注意:这里的粒子是同时跟踪自己的历史最优值与全局(群体)最优值来改变自己的位置预速度的,所以又叫做
全局版本的标准粒子群优化算法。
剩余21页未读,继续阅读
jason19821201
- 粉丝: 1
- 资源: 3
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- zigbee-cluster-library-specification
- JSBSim Reference Manual
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论6