PPP-RTK定位详解_ppp-rtk技术原理,ppp-rtk

5星 · 超过95%的资源需积分: 50 4.5k 浏览量更新于2023-03-16 评论 11 收藏 228KB PDF 举报

身份认证购VIP最低享 7 折!

领优惠券(最高得80元）

资源详情

资源评论

资源推荐

PPP-RTK: Precise Point Positioning Using

State-Space Representation in RTK Networks

Gerhard Wübbena, Martin Schmitz, Andreas Bagge,

Geo++



, Gesellschaft für satellitengestützte geodätische und navigatorische Technologien mbH

D-30827 Garbsen, Germany

BIOGRAPHY

Dr. Gerhard Wübbena received his degrees in geodesy

from the Universität Hannover. He has worked in the field

of GNSS since 1983. In 1990 he founded the company

Geo++

, which develops satellite navigation and

positioning software and systems. Among these are the

post-processing system GEONAP and the realtime system

GNSMART.

Dr. Martin Schmitz received his degrees in geodesy from

the Universität Hannover. He has been working in the

field of GNSS for the industry and as a research fellow at

the Universität Hannover since 1991.

Andreas Bagge graduated in geodesy at the Universität

Hannover. Since 1986 he is working in the field of GNSS,

at first for several years at the Universität Hannover, and

now at Geo++

All authors are currently employed at Geo++

. They are

concerned with research and development in satellite

positioning. Current projects focus on highly precise RTK

phase positioning (GNSMART), absolute GNSS antenna

field calibration, GNSS station calibration projects and

realtime attitude systems.

ABSTRACT

The concept of precise point positioning (PPP) is currently

associated with global networks. Precise orbit and clock

solutions are used to enable absolute positioning of a

single receiver. However, it is restricted in ambiguity

resolution, in convergence time and in accuracy. Precise

point positioning based on RTK networks (PPP-RTK) as

presented overcomes these limitations and gives

centimeter-accuracy in a few seconds.

The primary task in RTK networks using the Geo++

GNSMART software is the precise monitoring and

representation of all individual GNSS error components

using state-space modeling. The advantages of state-space

modeling are well known for PPP applications. It is much

closer to the physical error sources and can thus better

represent the error characteristics. It allows to better

separate the various error sources to improve performance

and can lead to much less bandwidth for transmission.

With RTK networks based on GNSMART it is possible to

apply the PPP concept with high accuracy. Ambiguity

resolution within the RTK network is mandatory and

allows the precise modeling of the system state. Since the

integer nature of the carrier phase ambiguities is

maintained, all error components can be consistently

modeled and give full accuracy in an ambiguity fixing

GNSS application.

For today's realtime applications, observations of a

reference station together with network derived parameters

to describe distance dependent errors or a virtual reference

station are transmitted to GNSS users in the field using the

RTCM standards. This can be termed as representation in

observation space (Observation Space Representation:

OSR). In contrast to this, also the actual state-space data

Presented at the 18

International Technical Meeting, ION GNSS-05, September 13-16, 2005, Long Beach, California.

can be used for the representation of the complete GNSS

state (State Space Representation: SSR). Hence, precise

absolute positioning based on a RTK network (PPP-RTK)

using state-space data is a practicable concept.

In principle, the concept can be applied to small, regional

and global networks. A reference station separation of

several 100 km to achieve ambiguity resolution and

therefore the key-issue to PPP-RTK is already possible

with GNSMART.

The complete transition from observation-space to state-

space requires the definition of adequate formats and

standardized models to provide the state-space data for

GNSS application. A single receiver then can position

itself with centimeter-accuracy within a few seconds in

post-processing and realtime applications. In between,

state-space data can still be used to generate data in

observation-space, e.g. RTCM or RINEX format, through

a conversion algorithm.

The state-space concept and pre-requisites are discussed.

The benefits of state space representation of GNSS errors

and their applications are pointed out.

INTRODUCTION

Global Navigation Satellite System (GNSS) applications

serve different kinds of applications and accuracies in

navigation and positioning. The number of applications is

steadily increasing as well as the demand for precise

navigation and positioning. GNSS applications generally

provide

• absolute positioning

• differential positioning

• precise absolute (point) positioning

Absolute GNSS positioning is the basic mode of an GNSS

and uses one single receiver for navigation and

positioning. At least two simultaneously operating stations

are required for differential GNSS positioning. It makes

use of the spatial correlation of systematic errors between

stations to estimate or reduce their effects in order to

achieve much higher accuracy.

Precise absolute positioning is a quite new category, which

is associated with the term precise point positioning (PPP)

(Zumberge et al 1997). It is a combination of the original

absolute positioning concept and differential positioning

techniques. PPP also uses observation data of a single

receiver and additionally state information on individual

GNSS errors derived from a GNSS network.

In current applications, precise absolute positioning is

applied in post-processing e.g. using IGS products, or

using a global network in realtime (Mullerschoen et al

2001). IGS products like precise satellite orbits and clocks

are actually state information on particular GNSS errors.

The mathematical model of PPP uses undifferenced, dual-

frequency observations and applies among other

corrections the precise orbit and clock data. The receiver

clock and tropospheric error are estimated, while the

ionosphere is eliminated using the ionospheric free linear

combination (L0).

PPP is limited in accuracy, because the ionospheric free

linear combination is currently mandatory. Accurate

ionospheric models are generally not available. Since the

ionospheric free linear combination is not based on integer

coefficients and the state information currently does not

preserve the integer nature of ambiguities, it is not

possible to resolve ambiguities adequately to access the

full GNSS carrier phase accuracy levels. Therefore long

integration or observation times are required for PPP.

The limitations of PPP can be overcome with RTK (Real

Time Kinematic) networks using state space modeling.

Such RTK networks can consistently derive all individual

GNSS errors in realtime. The atmospheric GNSS effects

are modeled and state information is also present for

ionosphere and troposphere. The complete state

information is ready for distribution to users in realtime.

As a consequence, users are capable to resolve ambiguities

and to achieve the known RTK accuracy level.

This concept of precise absolute positioning enabling

ambiguity resolution is the synthesis of the known precise

point positioning and network RTK. In the following it is

termed as PPP-RTK: Precise Point Positioning-RTK. The

main characteristics and differences of PPP and PPP-RTK

are listed in Tab. 1.

RTK NETWORKING

Precise positioning with GNSS requires the knowledge of

(the sum of) all error components with a corresponding

accuracy for the desired accuracy. The highest accuracy is

demanded by RTK applications, which require the

resolution of GNSS carrier phase ambiguities to gain

accuracy at the centimeter-level. Hence, RTK positioning

PPP PPP-RTK

network size global local/regional/

global

primary state information

satellite orbits provided provided

satellite clocks provided provided

ionosphere corrected provided

troposphere estimated provided

receiver clock estimated estimated

phase ambiguities & signal

L1 / L2 / L0 - / - / + + / + / +

integration time 30 ... 1800 s 10 ... 50 s

accuracy

static 3D ~ 5 cm 1 ... 3 cm

RTK 3D 15 ... 20 cm 1 ... 3 cm

Tab. 1 Characteristics of PPP and PPP-RTK

requires the knowledge of all error components with

accuracy definitely better than 1 cm to enable a RTK

service. The main error sources of GNSS are

• satellite and receiver clock

• satellite orbit

• ionosphere

• troposphere

• receiver antenna phase variations (PCV)

• multipath

The different GNSS error components do have different

characteristics. Satellite orbit, ionosphere and troposphere

are spatially correlated and it is therefore possible to

determine the effects in differential GNSS processing.

However, the effects decorrelate with distance and

introduce a distance dependent error into processing

results. The clock errors are estimated or eliminated in the

modeling approach of the GNSS data processing. Antenna

phase variations and multipath are station dependent errors

and must either be corrected or be adequately accounted

for.

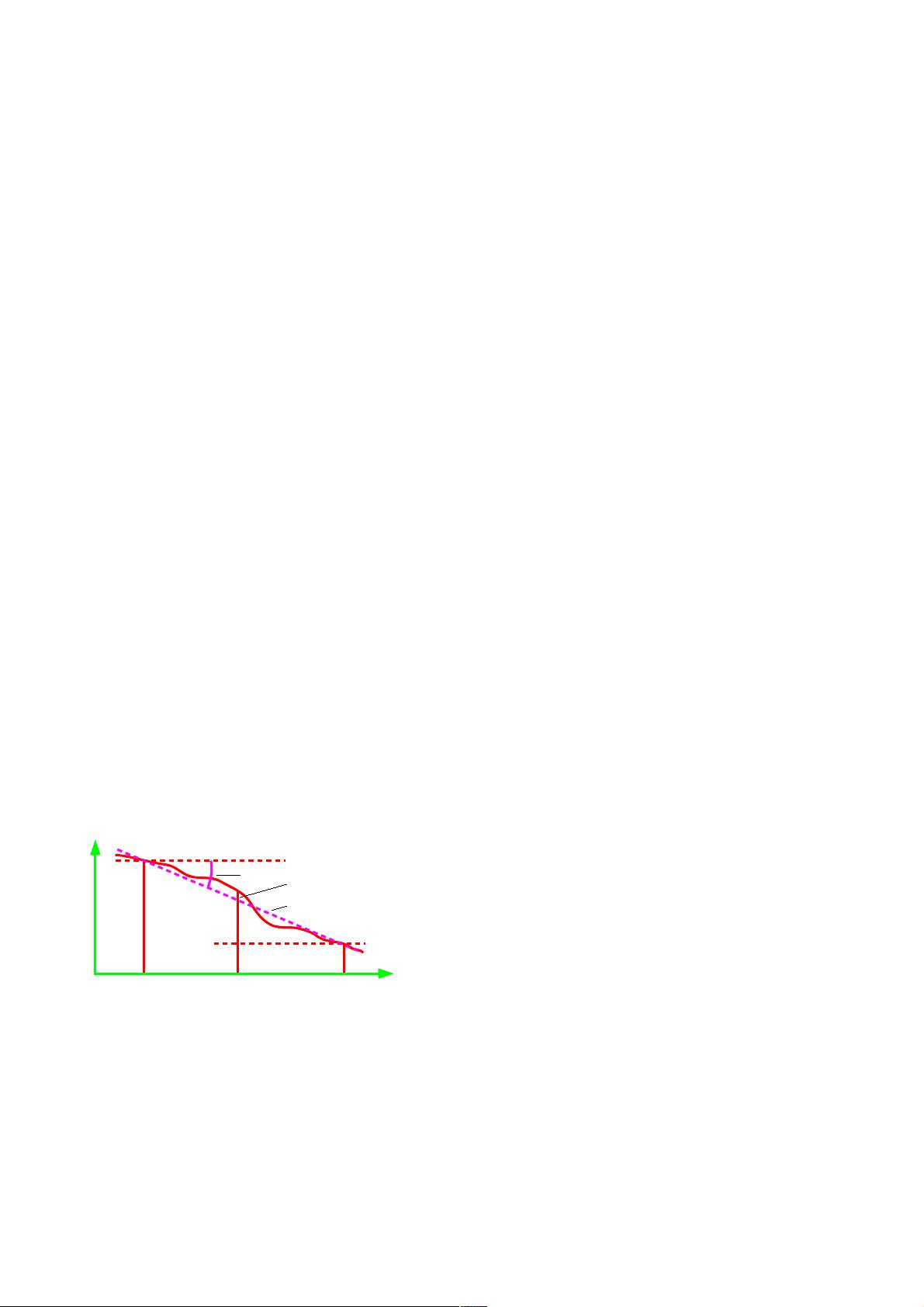
The principle of RTK networking is depicted in Fig. 1.

The GNSS errors e may be determined based on a single

reference station. However, the distance dependent error

cannot be determined by a single reference station, and its

correction data is not exactly valid for a user's position

(rover).

The distance dependent GNSS errors are the main limiting

factors in differential GNSS realtime applications.

Therefore multiple reference stations are combined in an

RTK network to determine primarily the distance

dependent GNSS errors and provide correction

information to enhance the positioning capabilities and

accuracies for a user in the field. In Fig. 1 the RTK

network is represented by two reference stations, which

enables the determination of distance dependent errors

(depicted as a simple linear interpolation between

reference stations).

The modeling approach of GNSS is an important aspect

for the different tasks in RTK networking. On the one

hand, simplified models are easily implemented, but will

show in the long run disadvantages in performance. On the

other hand, a rigorous approach is more complex.

However, the ideal approach is a complete state space

modeling (SSM).

GNSS-SMART: STATE MONITORING AND

REPRESENTATION TECHNIQUE

RTK networking is utilized in a rigorous and fundamental

way in the Geo++

GNSMART software. GNSS-SMART

stands for State Monitoring And Representation

Technique describing the essential concept, while

GNSMART is the actual Geo++

software implementation

of this technique. The GNSS errors must be precisely

modeled and monitored to resolve ambiguities as a

primary task. For any time and location within the

covered network area sophisticated services must provide

information on the GNSS errors based on the state

monitoring. The methods for this secondary task are

generally termed “representation technique”.

A complete state space model with millimeter-accuracy is

implemented for the rigorous and simultaneous adjustment

of GNSS observables, which is essential for the primary

task. The state space modeling follows the idea to model

the actual error sources instead of handling the effects of

the errors. The error effects belong to the observation

space, while the error sources are associated with the state

space. All error sources build up the state space model

(SSM). The state space model consists of

• model algorithms

• model parameters

The state space models applied in GNSMART are often

multiple step models. The models generally consist of a

functional model based on dynamic processes with

temporal and/or spatial stochastic properties. Alternatively

static parameters are used, when suited for the actual

physical condition. Further enhancements are achieved by

applying additional stochastic models with temporal

and/or spatial characteristics to describe remaining effects

not accounted for in the functional models. Tab. 2 lists the

functional and stochastic models currently implemented

and typically used in GNSMART. The actual applied

models and model parameters are configurable in

GNSMART.

The model parameters itself consist of

• state vector of unknown parameters

• complete variance/covariance matrix

of unknown parameters

This already indicates, that an ideal representation should

also contain stochastic properties. It is advantageous for

any application to decide on the quality of service. But

stochastic also express correlations between parameters.

To determine the (error) state of a GNSS system,

GNSMART estimates the following state parameters:

• satellite clock synchronization error

• satellite signal delays (group delays)

• satellite orbit error (kinematic orbits)

• ionospheric signal propagation changes

• tropospheric signal delays

Fig. 1: RTK networking and OSR principle, representation

error (FKP, VRS, PRS) for linear approximation

phase correction

distance

ref

rover

FKP

ref

rover

FKP

d representation error

linear approximation

剩余10页未读，继续阅读

pluck-songer

2019-04-13

还行，在下一次

honghong888555

粉丝: 1
资源: 2

会员权益专享

PPP-RTK 定位详解

评论3

会员权益专享

最新资源

PPP-RTK 定位详解

评论3

ppp-rtk开源软件

PPP、RTK、PPP-RTK

ppp-rtk技术原理

GNSS-PPP和RTK定位原理

一种高精度的GPS-RTK定位技术设计与实现

gps-rtk基本原理

rtk 定位 算法 matlab

rtk定位技术与机器视觉结合

RTK定位算法原理及程序

rtk定位算法如何实现

python RTK实现图片定位

rtk与机器视觉怎么结合

千寻位置rtk使用教程

RTKLib完整学习笔记

基于扩展卡尔曼滤波算法 用RTK数据对IMU进行校准的伪代码

RTK cors怎么用

RTK技术原理，请详细举例

三极管放大电路之单管放大器的仿真设计

会员权益专享

最新资源

rtk 定位算法 matlab

基于扩展卡尔曼滤波算法用RTK数据对IMU进行校准的伪代码