Variational Mode Decomposition.pdf

VMD

需积分: 33 156 浏览量更新于2023-03-16 收藏 3MB PDF 举报

2014年，K. Dragomiretskiy and D. Zosso, Variational Mode Decomposition等人提出 Variational Mode Decomposition,(VMD).

IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 62, NO. 3, FEBRUARY 1, 2014 531

Variational Mode Decomposition

Konstantin Dragomiretskiy and Dominique Zosso, Member, IEEE

Abstract—During the late 1990s, Huang introduced the algo-

rithm called Empirical Mode Decomposition, w hi

ch is widely

used today to recursively decompose a signal into different modes

of u nknown but separate spectral bands. EMD is known for

limitations like sensitivity to noise and sa

mpling. These limitations

could only partially be addressed by more mathematical attempts

to this decomposition problem, like synchrosqueezing, empirical

wavelets or recursive variational de

composition. Here, we propose

an entirely non-recursive variational mode decomposition model,

where the modes are extracted concurrently. The model looks

for an ensemble of modes and their re

spective center frequen-

cies, such that the modes collectively reproduce the input signal,

while each being smooth after demodulation into baseband. In

Fourier domain, this correspond

s to a narrow-band prior. We

show important relations to Wiener ﬁ lter denoising. Indeed, the

proposed method is a generalization of the classic Wiener ﬁlter

into multiple, adaptive ba

nds. Our model provides a solution

to the decomposition problem that is theoretically well founded

and still easy to understand. The variational model is efﬁciently

optimized using an alter

nating direction method of multipliers

approach. Preliminary results show attractive performance with

respect to existing mode decomposition models. In particular,

our proposed model is m

uch more robust to sampling and noise.

Finally, we show promising practical decomposition results on a

series of artiﬁcial and real data.

Index Terms—AM-FM, augmented Lagrangian, Fourier trans-

form, Hilbert transform, mode decomposition, spectral decompo-

sition, variational problem, Wiener ﬁlter.

I. INTRODUCTION

MPIRICAL MODE decompo sito n (EMD) proposed by

Huang et al. [1] is an algorithmic method to detect and de-

compose a signal into principal “modes”. This algorithm recur-

sively detects local minima/maxima in a signal, estimates lower/

upper envelopes by interpolation of these extrema, removes the

average of the envel opes as “low-pass” centerlin e, thus isolating

the high-frequency oscillations as “mode” of a s ign a l, and con-

tinues recursively on the remain ing “low-pass” centerline. I n

some cases, this sifting algorithm does indeed decompose a

signal into principal modes, how ever the resulting decomposi-

Manuscript received April 10, 2013; revised August 09, 2013; acce pted

October 10, 2013. Date of publication November 05, 2013; date of current

version January 13, 2014. The associate e ditor coordinating the review of this

manuscript and approving it for publication was Dr. Akbar Sayeed. This work

was supported by the Swiss National Science Foundation (SNF) by Grants

PBELP2_137727 and P300P2_147778, the W. M. Keck Foundation, ONR

Grants N000141210838 and N000141210040, and NSF Grant DMS-1118971.

The auth or s are with the Department of Mathematics, University of

California, Los Angeles (UCLA), Los Angeles, CA 90095 USA (e-mail:

konstantin@math.ucla.edu; zosso@math.ucla.edu).

Color versions of one or more of the ﬁgures in this paper are available online

at http://ieeexplore.ieee.org.

Digital Object Identiﬁer 10.1109/TSP.2013.2288675

tion is highly dependent on methods of extremal point ﬁnding,

interpolation of extremal p oints into carrier envelopes, and the

stopping criteria impo sed. The lack of mathem atical theory and

the aformention ed degrees of freedom reducing the algorithm’s

robustness all leave room for theoretical d evelopment and im-

provement on the robustness of the decomposition [2]– [5]. In

some experim ents it has been shown that EMD shares im por-

tant sim ilarities with wavelets and (adaptive) ﬁlter banks [6].

Despite the limited mathematical understanding and some

obvious shortcomings, the EMD method has had signiﬁcant im-

pact and is widely used in a broad variety of time-frequency

analysis applications. These involve signal deco mposition in

audio engineering [7], climate analysis [8], and various ﬂux,

respiratory, and neuromuscular signals found in medicine and

biology [9]–[12], to name just a few examples.

A. What is a Mode?

In the original EMD description, a mode is deﬁned as a signal

whose number of local extrema and zero-crossin gs differ at most

by on e [1]. In most later related works, the deﬁnition is slightly

changed into so-called Intrinsic Mode Functions (IMF), based

on modulation criteria:

Deﬁnition 1: (Intrinsic Mode Function): Intrinsic Mode

Functions are amplitude-modulated-frequen cy-m odulated

(AM-FM) signals, written as:

(1)

where the phase

is a non-decreasing function,

, the envelope is n on-negative , and, very impor-

tantly, both the envelope

and the instantaneous frequency

vary much slower than the phase [13],

[14].

In other words, on a sufﬁciently long interval

, the mode can be considered to be a pure har-

monic sign a l with amplitude

and instantaneous frequency

[13]. Note that the newer d eﬁnition of signal components

is slightly more restrict ive th a n the original one: while all sig-

nals adhering to the above IMF deﬁnition satisfy the original

EMD mode prop erties, the converse is not necessarily true [13].

The immediate consequence of the newer IMF deﬁnition, how-

ever, is limited bandwidth, as we show in the next paragraphs,

and which is the central assumption that allows m ode separa-

tion in the proposed v ariation al mode decom position model.

Our restricted class of admissible mode functions is also mo-

tivated by analysis in [3], for they are well-behaved with re-

spect to tim e-frequency analysis of extracted modes, as rou-

tinely pe rf or med in the Hi lber t-Huang-Transform [1]. In con-

trast, the original IMF deﬁnition also admits non-

and dis-

continuous signals like the sawtooth, for wh ich the estimated in-

stantaneous frequency is not ph ysically m eanin gfu l, see Fig. 1.

See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.

532 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 62, NO. 3, FEBRUARY 1, 2014

Fig. 1. Sawtooth signal and its phase/frequency. (a) The original signal. (b) The

estimated phase after Hilbert transform. The phase exhibits jumps at the dis-

continuous saw-peaks. (c) The instantaneous frequency is obtained as the time-

derivative of the phase. At the discontinuous saw-peaks, this is clearly mean-

ingless. Such a signal is an admissible mode according to the original IMF def-

inition based on zero-crossings and local extrema [1], but not part of the newer

deﬁnition based on amplitude- and frequency-modulated signals (1) w h ich is

also used here [13].

Indeed, if is the mean frequency of a mod e, then its prac-

tical bandwidth increases both with the maximum deviation

of the instantaneous frequency from its center (carrier fre-

quency,

), and with the rate of this excursion, , according

to Carson’s rule

[15]:

(2)

In addition to this, the bandwidth of the envelope

modu-

lating the am plitude of the FM signal, it self given by its highest

frequency

, broadens the spectrum even further:

Deﬁnition 2: (Total Practical IMF Bandwidth): We esti-

mate the total practical bandwidth of an I MF as

(3)

Depending on the actual IMF, either of these terms may be dom-

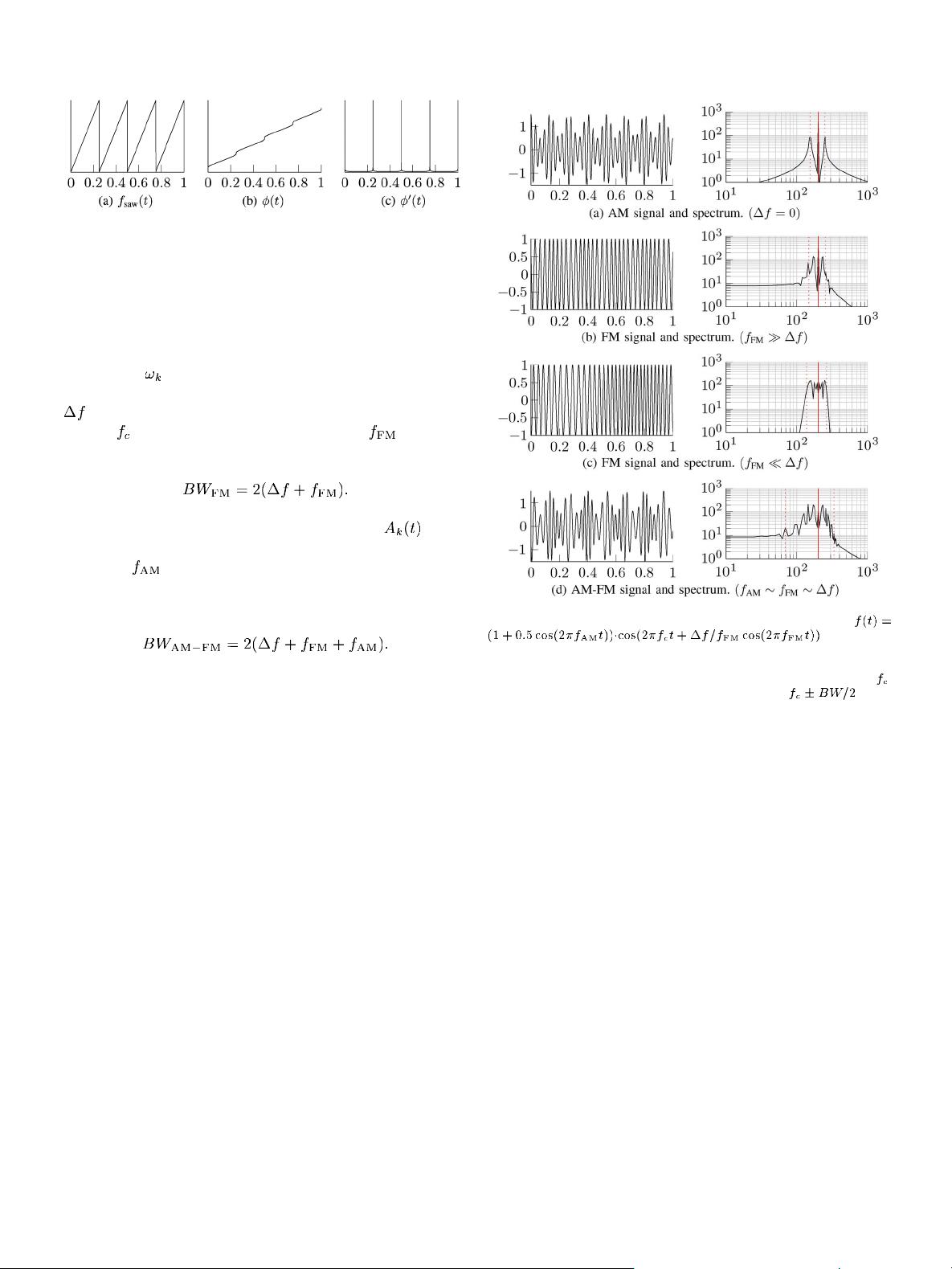
inant. An illustration o f four typical cases is provided in Fig. 2,

where the last example is rather extrem e in term s of required

bandwidth (for illustratio nal purposes).

B. Recent Work

To address the sensitivity of the original EMD alg orithm with

respect to noise and s ampling, more robust versions have since

been proposed [16], [17]. T here, in essence, the extraction of

local extrema and their interpolation for envelope forming is

substituted by more robust constraint optimization techniques.

The global r ecur sive sifting structur e of EMD is maintained,

however.

Other authors create a partially variational approach to EMD

where the signal is explicitly modeled as an IMF [18]. This

method still relies on in terpolation, selection of a Fourier low-

pass ﬁlter, and siftin g of high-frequency components. Here, the

candidate m odes are extracted variatio nally. The sig nal is re-

cursively decomposed into an IMFwithTV3-smoothenvelope

(3rd-order total variation), and a T V3- smooth residual. The re-

sulting algorithm is very similar to EMD in structure, but some-

what more robust to noise.

A slightly more variational, but still recursive decomposi-

tion scheme has been proposed in [19], for the analysis o f time-

varying vibration. Here, the dominant vibration is extracted

The theoretical spectral support of a frequency modulated signal is inﬁnite;

However, for practical purposes, Carson’s rule p rovides boun ds containing 98%

of the signal’s power, which should be good enough in this context.

Fig. 2. AM-FM signals with limited bandwid th. Here, w e use a signal

.(a)PureAM

signal. (b) Pure FM signal with little but rapid frequency deviations. (c) Pure FM

signal with slow but important frequency oscillations. (d) Co mb in ed AM-F M

signal. The solid vertical line in the spectrum shows the carrier frequency

the dotted lines corr espond to the estimated band limits at

, based

on (3).

by est im a ting its instantane ous frequency as average frequency

after the Hilbert transform. Again, this process is r epeated re-

cursively on the residual signal.

A third class of methods makes use of wavelets. An ap-

proach based on selecting appropriate wavelet scales, dubbed

synchrosqueezing, was proposed by Daubechies et al. [13],

[20]. They remove unimpo rtan t wavelet coefﬁcients (both in

time and scale) by thresholding of the respective signal ene rgy

in that portion. Conversely, locally relevant wavelets are se-

lected as local m axim a of the continuous wavelet transform,

that are shown to be tuned with the local signals, and from

which the current instantaneous frequency of each m ode can

be recovered.

Other recent work pursuing the same goal is the E mpirical

Wavelet Transform (EWT) to explicitly build an ad apti ve

wavelet basis to decompose a given signal into ada ptive sub-

bands [14]. This mo del relies on robust preprocessing for

peak detection, then performs spectrum segmentation based on

detected maxima, and constructs a corresponding wavelet ﬁlter

bank. The ﬁlter bank includes ﬂexibility for some molliﬁcation

(spectral overlap), but explicit construction of frequency bands

still appears slightly strict.

Finally, a related decomposition into different wavelet bands

was suggested by [21]. The author introduces two complemen-

tary wavelet bases with different Q -factor. This allows discrim-

DRAGOMIRETSKIY AND ZOSSO: VARIATIONAL MODE DECOMP OSITION 533

inating between sustained oscillations (high-reson ance compo-

nents), and non-oscillatory, short-term transients. Indeed, the

high-resonance components can sparsely be represen ted in a

high-Q w avelet basis, while transients will be synthesized by

low-Q wavelets.

C. Pro posed Method

In this paper, we propose a new, fully intrin sic a nd adap-

tive, variational m ethod, the min imization of wh ich leads to

a decomposition of a signal into its principal modes. Indeed,

the c ur rent decomposition models are mostly lim it ed by 1)

their algorithmic ad-hoc nature lacking mathem atical theory

(EMD), 2) the recursive sifting in most methods, which does

not a llo w for backward error correction, 3) the inability to

properly cope with noise, 4) the hard band-limits of wavelet

approaches, and 5) the requirem ent of predeﬁning ﬁlter bank

boundaries in EWT. In co ntrast, we prop ose a variation al model

that determines the relevant bands adaptively, and estimates

the co rrespon din g modes concurrently, thus properly balancing

errors between them. Motivated by the narrow-band properties

corresponding to the current common IMF deﬁnition, we look

for an ensemble of m odes that reconstruct the given inpu t signal

optimally (either exactly, or in a least-squares sense), while

each being band-limited about a center frequency estimated

on-line. Here, o ur variational model speciﬁcally can address the

presence of noise in the in put signal. I ndeed , the tight relations

to the Wiener ﬁlter actually suggest that our approach has

some optimality in dealing with noise. The vari ational m od el

assesses the bandwidth of the modes as

-norm, after shifting

the Hilbert-complemented, analytic signal down into b ase-

band by comp lex harmonic mixing. The resulting optimization

scheme is very simple and fast: each mode is iteratively updated

directly in Fourier domain, as the narrow-band Wiener ﬁlt er

corresponding to the current estimate of the mode’s center-fre-

quency being applied to the signal estimation residual of all

other modes; then the center frequency is re-estimated as the

center-of-gravity of the mode’s power spectrum . Our quanti-

tative results o n tone detection and separation show excellen t

performance irrespective of harmonic frequencies, in particular

when compared to the apparent limits of EMD in this respect.

Further, qualitative results on synthetic and real test signals are

convincing, also regarding robustness to signal noise.

The rest of this paper is organized as follows: Section II intro-

duces the no tions of the Wiener ﬁlter, the Hilbert transform, and

the analytic signal. Also, we brieﬂy review the concept of fre-

quency shifting throug h harmonic m ixing. These concepts are

the very building blocks of our variational mode decomposition

model. Although signal processing scholars can be expected to

be familiar with these concepts, we include this short refresher

to keep the manuscript largely self-contained and accessible to

readers of different provenience. Section III presents and ex-

plains our variational model in detail, our algorithm to mini-

mize it, and ﬁner technicalities on optimization, boundaries and

periodicity. Section IV contains our experiments and results,

namely some simple quant itat ive performance evaluation s, and

comparisons to EMD, and various synthetic multi-mode signals

and our method’s decomposition of them. Speciﬁcally, tone de-

tection and separation, as well as n oise robustness will be an-

alyzed and compared to that of EMD. Additionally, real sig-

nals will be considered. Section V concludes on our proposed

variational mode decomposition method, summarizes again the

main assumptions and limitatio ns, and inclu des some future di-

rections and expected improvem ents.

II. T

OOLS FROM SIGNAL PROCESSING

In this section we brieﬂy review a few concepts and tools

from signal processing that will constitute the building blocks

of our variational mode decomposition model. First, we present

a classical case of Wiener ﬁltering for denoising. Next, w e de-

scribe the Hilbert transform and its use in the construction of a

single-side band analytic signal. Finally, we sho w how multi-

plication with pure complex harmonics is used to shift the fre-

quencies in a signal.

A. Wiener Filtering

Let us start with a sim ple denoising problem. Consider the

observed signal

, a copy of the original signal affected

by additive zero-mean Gau ssian noise:

(4)

Recovering the unknown signal

is a typical ill-posed inverse

problem [22], [23], classically addressed using Tikhonov regu-

larization [24], [25]:

(5)

of which the Euler-Lagrange equatio ns are easily obtained and

typically solved in Fourier domain:

(6)

where

,with

, is the Fourier transform of the signal . Clearly,

the recovered signal

is a low-pass narrow-band selection of

the input signal

around . Indeed, the solution corre-

sponds to convolution with a Wiener ﬁlter, where

represents

the variance of the white noise, and the signal has a lowpass

power spectrum prior [26], [27].

B. Hilbert Transform and Analytic Signal

Here,wecitethedeﬁnition of the Hilbert transform given in

[28]:

Deﬁnition 3: (Hilbert Transform): The 1-D Hilbert trans-

form is the lin ear, shift-inv arian t operator

that maps all 1-D

cosine functions into their corresp ond ing sine functions. It is

an all-pass ﬁlter that is characterized by the transfer function

Thus, the Hilbert transform is a multiplier operator in

the spectral dom ain. The corresponding impulse response is

剩余13页未读，继续阅读

SparkQiang

粉丝: 62
资源: 123

Variational Mode Decomposition.pdf

变分模式分解Variational Mode Decomposition源码

变分模态分解

variational mode decomposition

emd,vmd分解代码

FeedbackVMD algorithm (FVMD)

vmd算法matlab

multivariate vmd

matlab 逐次变分模态分解

eemd和vmd的区别

svmd逐次变分模态分解

最新资源