C++求所有顶点之间的最短路径（用Dijkstra算法）_c++最短路径 - CSDN文库

C++所有顶点间最短路径

C++顶点间最短路径

C++最短路径

5星 · 超过95%的资源 14 浏览量更新于2023-03-16 评论 1 收藏 105KB PDF 举报

身份认证购VIP最低享 7 折!

领优惠券(最高得80元）

资源详情

资源评论

资源推荐

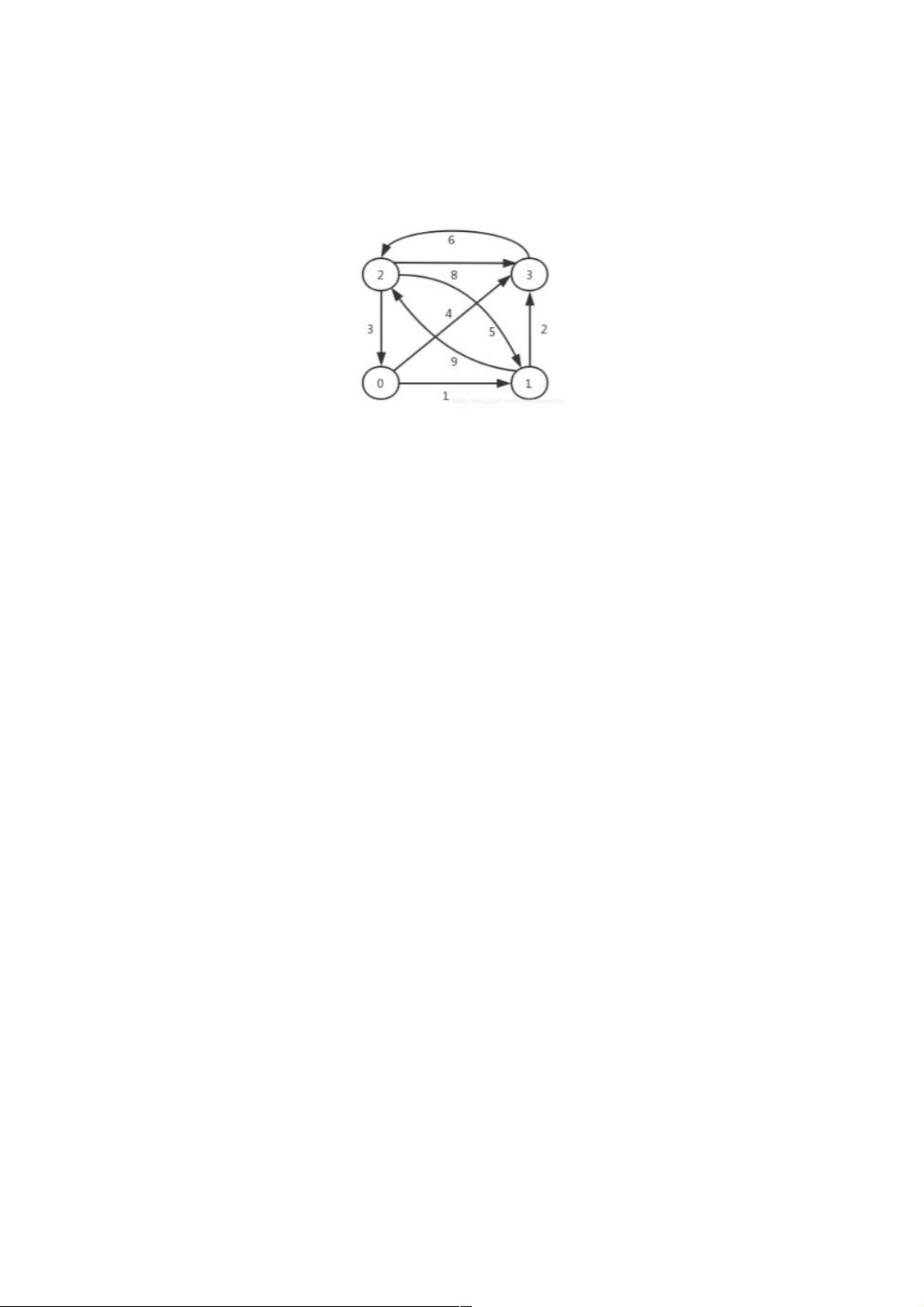
C++求所有顶点之间的最短路径（用求所有顶点之间的最短路径（用Dijkstra算法）算法）

主要为大家详细介绍了C++用Dijkstra算法求所有顶点之间的最短路径，文中示例代码介绍的非常详细，具有一

定的参考价值，感兴趣的小伙伴们可以参考一下

本文实例为大家分享了C++求所有顶点之间最短路径的具体代码，供大家参考，具体内容如下

一、思路：一、思路：不能出现负权值的边不能出现负权值的边

（1）轮流以每一个顶点为源点，重复执行Dijkstra算法n次，就可以求得每一对顶点之间的最短路径及最短路径长度，总的执

行时间为O(n的3次方）

（2）另一种方法：用Floyd算法，总的执行时间为O(n的3次方）（另一文章会写）

二、实现程序：二、实现程序：

1.Graph.h:有向图

#ifndef Graph_h

#define Graph_h

#include <iostream>

using namespace std;

const int DefaultVertices = 30;

template <class T, class E>

struct Edge { // 边结点的定义

int dest; // 边的另一顶点位置

E cost; // 表上的权值

Edge<T, E> *link; // 下一条边链指针

};

template <class T, class E>

struct Vertex { // 顶点的定义

T data; // 顶点的名字

Edge<T, E> *adj; // 边链表的头指针

};

template <class T, class E>

class Graphlnk {

public:

const E maxValue = 100000; // 代表无穷大的值（=∞）

Graphlnk(int sz=DefaultVertices); // 构造函数

~Graphlnk(); // 析构函数

void inputGraph(); // 建立邻接表表示的图

void outputGraph(); // 输出图中的所有顶点和边信息

T getValue(int i); // 取位置为i的顶点中的值

E getWeight(int v1, int v2); // 返回边（v1， v2）上的权值

bool insertVertex(const T& vertex); // 插入顶点

bool insertEdge(int v1, int v2, E weight); // 插入边

bool removeVertex(int v); // 删除顶点

bool removeEdge(int v1, int v2); // 删除边

int getFirstNeighbor(int v); // 取顶点v的第一个邻接顶点

int getNextNeighbor(int v,int w); // 取顶点v的邻接顶点w的下一邻接顶点

int getVertexPos(const T vertex); // 给出顶点vertex在图中的位置

int numberOfVertices(); // 当前顶点数

private:

int maxVertices; // 图中最大的顶点数

int numEdges; // 当前边数

int numVertices; // 当前顶点数

Vertex<T, E> * nodeTable; // 顶点表(各边链表的头结点)

};

// 构造函数:建立一个空的邻接表

本内容试读结束，登录后可阅读更多

下载后可阅读完整内容，剩余5页未读，立即下载

评论5

杏花朵朵

2023-07-29

这个文件将Dijkstra算法的应用场景举了一些实际的例子，让人能够更好地理解算法的实际应用。

weixin_38624315

粉丝: 7
资源: 921

会员权益专享

图片转文字

全年可省5，000元立即开通

最新资源

资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！点击此处反馈