没有合适的资源?快使用搜索试试~ 我知道了~
首页卷积神经网络入门到精通微篇
卷积神经网络入门到精通微篇
需积分: 50 77 下载量 170 浏览量
更新于2023-03-16
评论
收藏 2.48MB PDF 举报
卷积神经网络,是一种前馈神经网络,人工神经元可以响应周围单元,可以进行大型图像处理。卷积神经网络包括卷积层和池化层。 卷积神经网络包括一维卷积神经网络、二维卷积神经网络以及三维卷积神经网络。一维卷积神经网络常应用于序列类的数据处理;二维卷积神经网络常应用于图像类文本的识别;三维卷积神经网络主要应用于医学图像以及视频类数据识别。
资源详情
资源评论
资源推荐

卷积神经网络 CNN 从入门到精通
卷积神经网络算法的一个实现
前言
从理解卷积神经到实现它,前后花了一个月时间,现在也还有一些地方没有理解透
彻,CNN 还是有一定难度的,不是看哪个的博客和一两篇论文就明白了,主要还是靠
自己去专研,阅读推荐列表在末尾的参考文献。目前实现的 CNN 在 MINIT 数据集上效
果还不错,但是还有一些 bug,因为最近比较忙,先把之前做的总结一下,以后再继续
优化。
卷积神经网络 CNN 是 Deep Learning 的一个重要算法,在很多应用上表现出卓
越的效果,[1]中对比多重算法在文档字符识别的效果,结论是 CNN 优于其他所有的算
法。CNN 在手写体识别取得最好的效果,[2]将 CNN 应用在基于人脸的性别识别,效
果也非常不错。前段时间我用 BP 神经网络对手机拍照图片的数字进行识别,效果还算
不错,接近 98%,但在汉字识别上表现不佳,于是想试试卷积神经网络。
1、CNN 的整体网络结构
卷积神经网络是在 BP 神经网络的改进,与 BP 类似,都采用了前向传播计算输出
值,反向传播调整权重和偏置;CNN 与标准的 BP 最大的不同是:CNN 中相邻层之间
的神经单元并不是全连接,而是部分连接,也就是某个神经单元的感知区域来自于上层
的部分神经单元,而不是像 BP 那样与所有的神经单元相连接。CNN 的有三个重要的思
想架构:
局部区域感知
权重共享
空间或时间上的采样
局部区域感知能够发现数据的一些局部特征,比如图片上的一个角,一段弧,这些
基本特征是构成动物视觉的基础[3];而 BP 中,所有的像素点是一堆混乱的点,相互之
间的关系没有被挖掘。
CNN 中每一层的由多个 map 组成,每个 map 由多个神经单元组成,同一个 map
的所有神经单元共用一个卷积核(即权重),卷积核往往代表一个特征,比如某个卷积
和代表一段弧,那么把这个卷积核在整个图片上滚一下,卷积值较大的区域就很有可能
是一段弧。注意卷积核其实就是权重,我们并不需要单独去计算一个卷积,而是一个固
定大小的权重矩阵去图像上匹配时,这个操作与卷积类似,因此我们称为卷积神经网络,
实际上,BP 也可以看做一种特殊的卷积神经网络,只是这个卷积核就是某层的所有权
重,即感知区域是整个图像。权重共享策略减少了需要训练的参数,使得训练出来的模
型的泛华能力更强。
采样的目的主要是混淆特征的具体位置,因为某个特征找出来后,它的具体位置已
经不重要了,我们只需要这个特征与其他的相对位置,比如一个“8”,当我们得到了上
面一个"o"时,我们不需要知道它在图像的具体位置,只需要知道它下面又是一个“o”我
们就可以知道是一个'8'了,因为图片中"8"在图片中偏左或者偏右都不影响我们认识它,
这种混淆具体位置的策略能对变形和扭曲的图片进行识别。
CNN 的这三个特点是其对输入数据在空间(主要针对图像数据)上和时间(主要
针对时间序列数据,参考 TDNN)上的扭曲有很强的鲁棒性。CNN 一般采用卷积层与

采样层交替设置,即一层卷积层接一层采样层,采样层后接一层卷积...这样卷积层提取
出特征,再进行组合形成更抽象的特征,最后形成对图片对象的描述特征,CNN 后面
还可以跟全连接层,全连接层跟 BP 一样。下面是一个卷积神经网络的示例:
图 1(图片来源)
卷积神经网络的基本思想是这样,但具体实现有多重版本,我参考了 matlab 的 Deep
Learning 的工具箱 DeepLearnToolbox,这里实现的 CNN 与其他最大的差别是采样层没
有权重和偏置,仅仅只对卷积层进行一个采样过程,这个工具箱的测试数据集是 MINIST,
每张图像是 28*28 大小,它实现的是下面这样一个 CNN:
图 2
2、网络初始化
CNN 的 初始化主要是初始化卷 积 层 和输 出 层 的 卷 积 核 ( 权 重 ) 和 偏 置,
DeepLearnToolbox 里面对卷积核和权重进行随机初始化,而对偏置进行全 0 初始化。
3、前向传输计算
前向计算时,输入层、卷积层、采样层、输出层的计算方式不相同。
3.1 输入层:输入层没有输入值,只有一个输出向量,这个向量的大小就是图片的
大小,即一个 28*28 矩阵;
3.2 卷积层:卷积层的输入要么来源于输入层,要么来源于采样层,如上图红色部
分。卷积层的每一个 map 都有一个大小相同的卷积核,Toolbox 里面是 5*5 的卷积
核。下面是一个示例,为了简单起见,卷积核大小为 2*2,上一层的特征 map 大小为
4*4,用这个卷积在图片上滚一遍,得到一个一个(4-2+1)*(4-2+1)=3*3 的特征
map,卷积核每次移动一步,因此。在 Toolbox 的实现中,卷积层的一个 map 与上层
的所有 map 都关联,如上图的 S2 和 C3,即 C3 共有 6*12 个卷积核,卷积层的每一
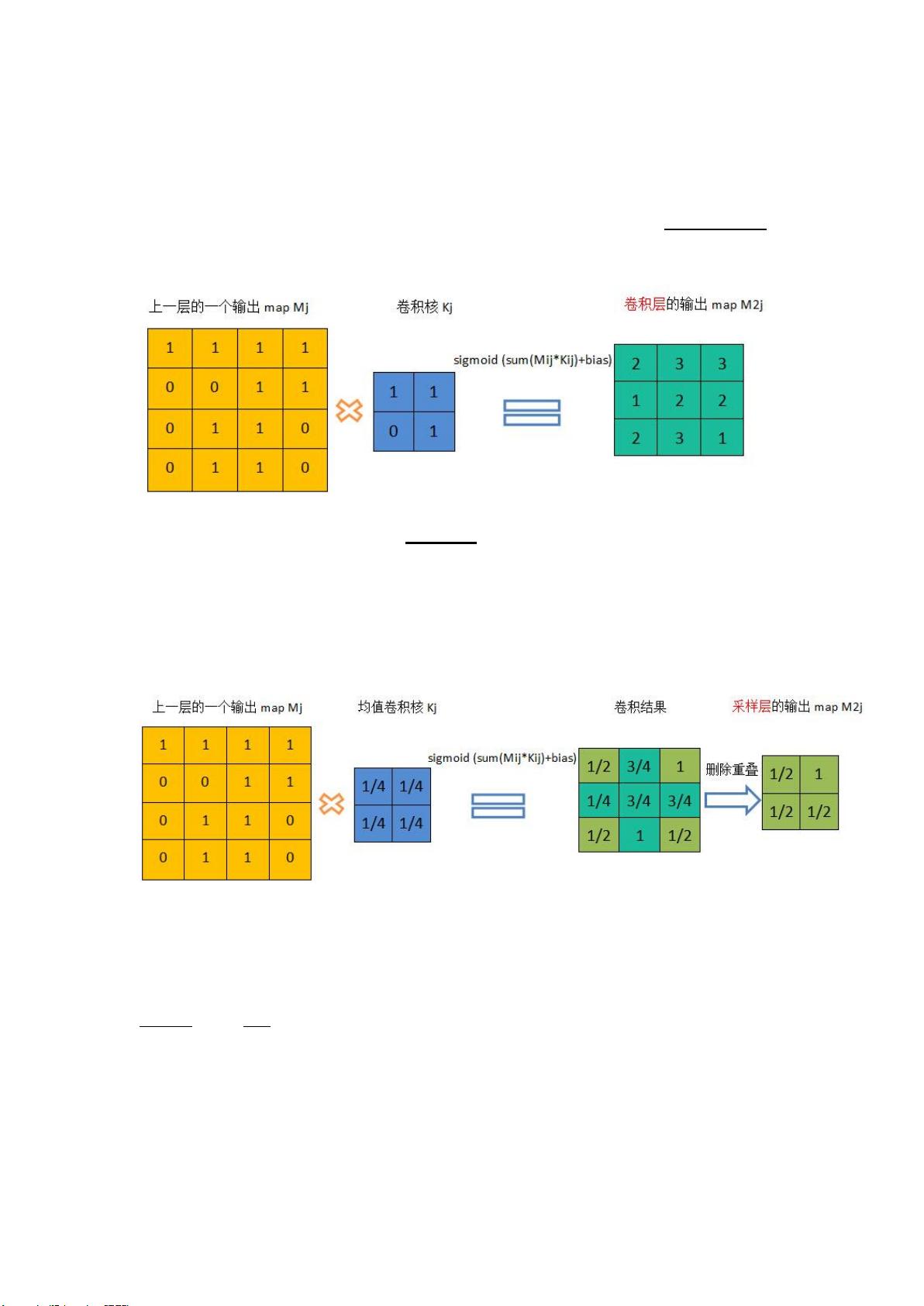
个特征 map 是不同的卷积核在前一层所有 map 上作卷积并将对应元素累加后加一个
偏置,再求 sigmod 得到的。还有需要注意的是,卷积层的 map 个数是在网络初始化
指定的,而卷积层的 map 的大小是由卷积核和上一层输入 map 的大小决定的,假设
上一层的 map 大小是 n*n、卷积核的大小是 k*k,则该层的 map 大小是(n-k+1)*(n-
k+1),比如上图的 24*24 的 map 大小 24=(28-5+1)。 斯坦福的深度学习教程更
加详细的介绍了卷积特征提取的计算过
程。
图 3
3.3 采样层(subsampling,Pooling):采样层是对上一层 map 的一个采样处
理,这里的采样方式是对上一层 map 的相邻小区域进行聚合统计,区域大小为
scale*scale,有些实现是取小区域的最大值,而 ToolBox 里面的实现是采用 2*2 小
区域的均值。注意,卷积的计算窗口是有重叠的,而采用的计算窗口没有重叠,ToolBox
里面计算采样也是用卷积(conv2(A,K,'valid'))来实现的,卷积核是 2*2,每个元素都
是 1/4,去掉计算得到的卷积结果中有重叠的部分,
即:
图 4
4、反向传输调整权重
反向传输过程是 CNN 最复杂的地方,虽然从宏观上来看基本思想跟 BP 一样,都
是通过最小化残差来调整权重和偏置,但 CNN 的网络结构并不像 BP 那样单一,对不
同的结构处理方式不一样,而且因为权重共享,使得计算残差变得很困难,很多论文
[1][5]和文章[4]都进行了详细的讲述,但我发现还是有一些细节没有讲明白,特别是
采样层的残差计算,我会在这里详细讲述。
4.1 输出层的残差
和 BP 一样,CNN 的输出层的残差与中间层的残差计算方式不同,输出层的残差是
输出值与类标值得误差值,而中间各层的残差来源于下一层的残差的加权和。输出层的
残差计算如下:

公式来源
这个公式不做解释,可以查看公式来源,看斯坦福的深度学习教程的解释。
4.2 下一层为采样层(subsampling)的卷积层的残差
当一个卷积层 L 的下一层(L+1)为采样层,并假设我们已经计算得到了采样层的残
差,现在计算该卷积层的残差。从最上面的网络结构图我们知道,采样层(L+1)的 map
大小是卷积层 L 的 1/(scale*scale), ToolBox 里面,scale 取 2,但这两层的 map
个数是一样的,卷积层 L 的某个 map 中的 4 个单元与 L+1 层对应 map 的一个单元关
联,可以对采样层的残差与一个 scale*scale 的全 1 矩阵进行克罗内克积进行扩充,
使得采样层的残差的维度与上一层的输出 map 的维度一致,Toolbox 的代码如下,其
中 d 表示残差,a 表示输出值:
net.layers{l}.d{j} = net.layers{l}.a{j} .* (1 - net.layers{l}.a{j}) .* expand(net.layers{l + 1}.d{j},
[net.layers{l + 1}.scale net.layers{l + 1}.scale 1])
扩展过程:
图 5
利用卷积计算卷积层的残差:
图 6
4.3 下一层为卷积层(subsampling)的采样层的残差
当某个采样层 L 的下一层是卷积层(L+1),并假设我们已经计算出 L+1 层的残差,
现在计算 L 层的残差。采样层到卷积层直接的连接是有权重和偏置参数的,因此不像卷
积层到采样层那样简单。现再假设 L 层第 j 个 map Mj 与 L+1 层的 M2j 关联,按照
BP 的原理,L 层的残差 Dj 是 L+1 层残差 D2j 的加权和,但是这里的困难在于,我们
很难理清 M2j 的那些单元通过哪些权重与 Mj 的哪些单元关联,Toolbox 里面还是采用

卷积(稍作变形)巧妙的解决了这个问题,其代码为:
convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), 'full');
rot180 表示对矩阵进行 180 度旋转(可通过行对称交换和列对称交换完成),为什么这
里要对卷积核进行旋转,答案是:通过这个旋转,'full'模式下得卷积的正好抓住了前向
传输计算上层 map 单元与卷积和及当期层 map 的关联关系,需要注意的是 matlab 的内
置函数 convn 在计算卷积前,会对卷积核进行一次旋转,因此我们之前的所有卷积的计
算都对卷积核进行了旋转:
a =
1 1 1
1 1 1
1 1 1
k =
1 2 3
4 5 6
7 8 9
>> convn(a,k,'full')
ans =
1 3 6 5 3
5 12 21 16 9
12 27 45 33 18
11 24 39 28 15
7 15 24 17 9
convn 在计算前还会对待卷积矩阵进行 0 扩展,如果卷积核为 k*k,待卷积矩阵
为 n*n,需要以 n*n 原矩阵为中心扩展到(n+2(k-1))*(n+2(k-1)),所有上面
convn(a,k,'full')的计算过程如下:
剩余82页未读,继续阅读
大锦
- 粉丝: 8
- 资源: 6
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
- SPC统计方法基础知识.pptx
- MW全能培训汽轮机调节保安系统PPT教学课件.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0