没有合适的资源?快使用搜索试试~ 我知道了~
首页Fundamentals Of Communication Systems答案
Fundamentals Of Communication Systems答案
需积分: 12 21 下载量 8 浏览量
更新于2023-03-16
评论 2
收藏 3.9MB PDF 举报
Proakis J.G., Salehi M.-Fundamentals Of Communication Systems答案
资源详情
资源评论
资源推荐

Solution Manual
Fundamentals of Communication Systems
John G. Proakis Masoud Salehi
Second Edition
2013
Proakis/Salehi/Fundamentals of Communications Systems 2E
© 2014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained
from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical,
photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle
River, NJ 07458.
Chapter 2
Problem 2.1
1. Π
(
2t +5
)
= Π
2
t +
5
2
. This indicates first we have to plot
Π(
2
t)
and then shift it to left by
5
2
. A plot is shown below:
6
−
11
4
−
9
4
-
t
Π
(
2t +5
)
1
2.
P
∞
n=0
Λ(t −n)
is a sum of shifted triangular pulses. Note that the sum of the left and right side
of triangular pulses that are displaced by one unit of time is equal to 1, The plot is given below
✲
✻
t
x
2
(t)
−1
1
3. It is obvious from the definition of sgn(t) that sgn(2t) = sgn(t). Therefore x
3
(t) = 0.
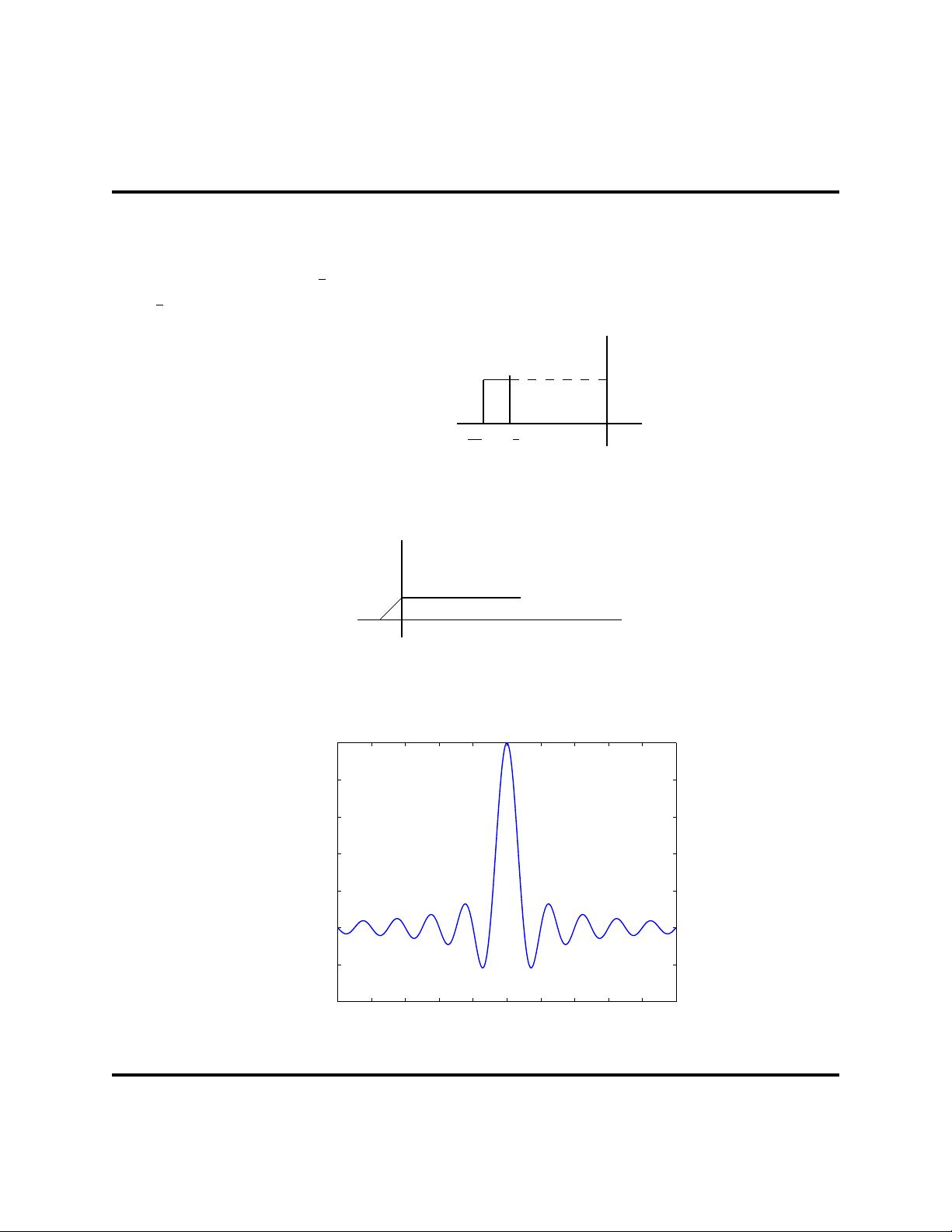
4. x
4
(t) is sinc(t) contracted by a factor of 10.
−1 −0.8 −0.6 −0.4 −0.2 0 0.2 0.4 0.6 0.8 1
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
3
Proakis/Salehi/Fundamentals of Communications Systems 2E
© 2014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained
from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical,
photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle
River, NJ 07458.
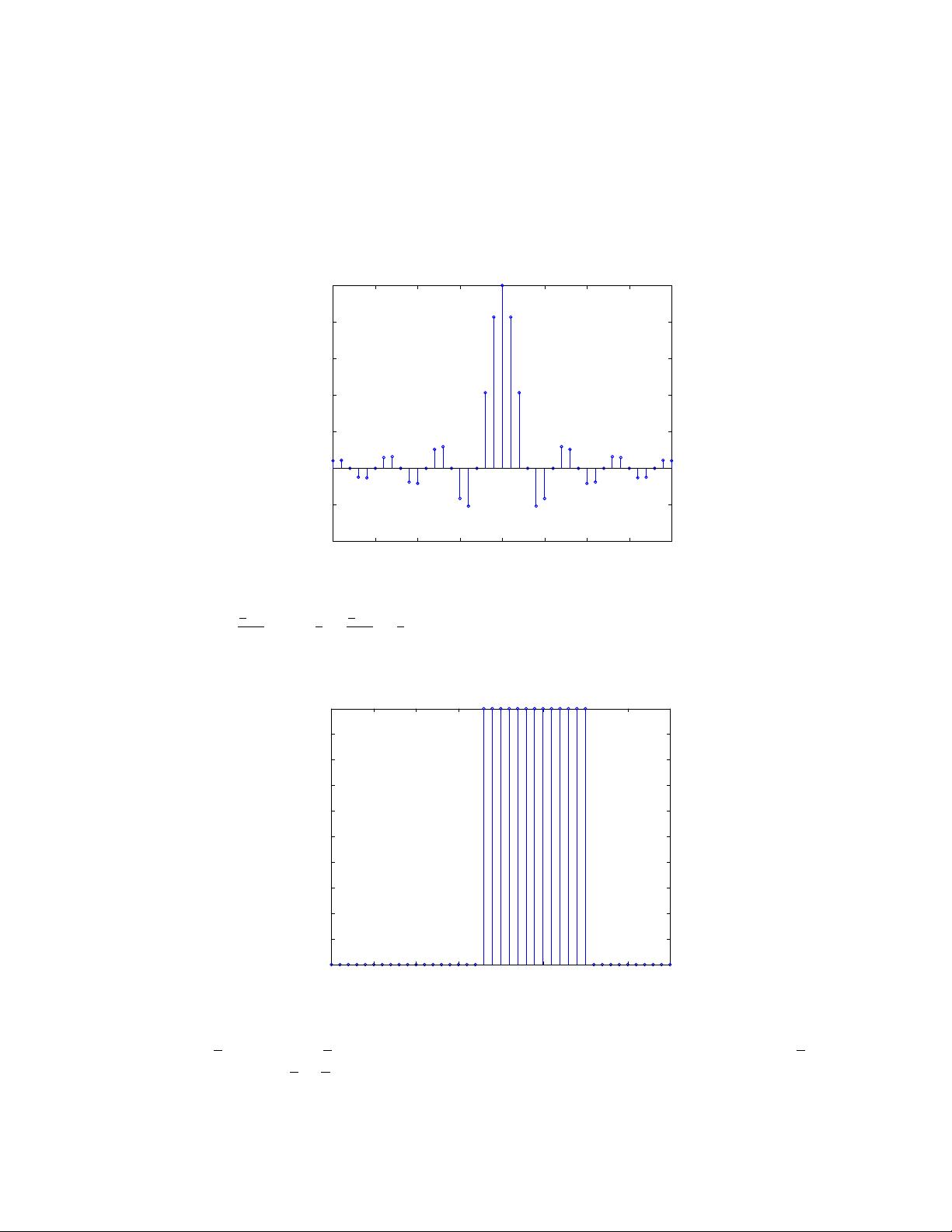
Problem 2.2
1. x[n] = sinc(3n/9) = sinc(n/3).
−20 −15 −10 −5 0 5 10 15 20
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
2. x[n] = Π
n
4
−1
3
. If −
1
2
≤
n
4
−1
3
≤
1
2
, i.e., −2 ≤ n ≤ 10, we have x[n] = 1.
−20 −15 −10 −5 0 5 10 15 20
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
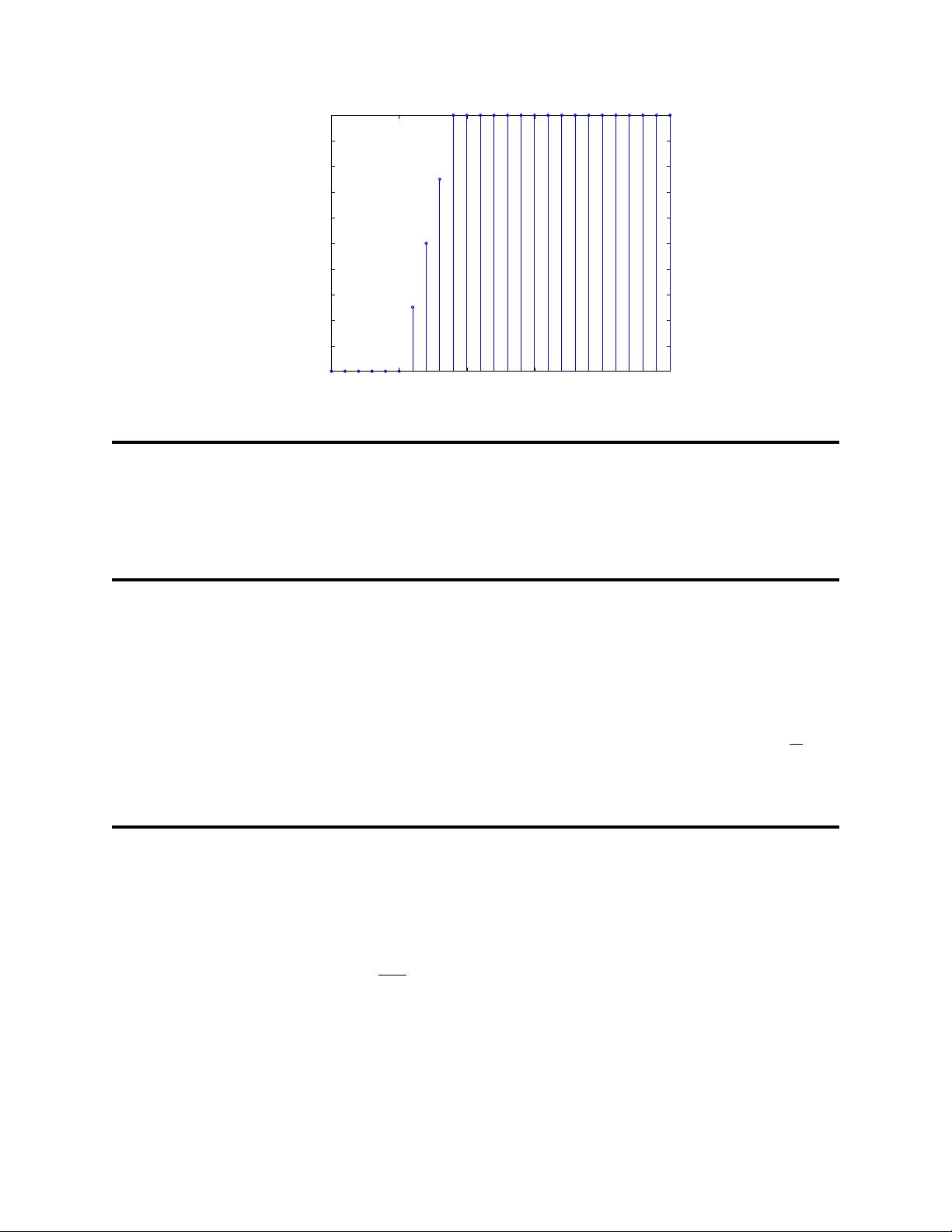
3. x[n] =
n
4
u
−1
(n/
4
) −(
n
4
−
1
)u
−1
(n/
4
−
1
)
. For
n <
0,
x[n] =
0, for 0
≤ n ≤
3,
x[n] =
n
4
and
for n ≥ 4, x[n] =
n
4
−
n
4
+1 = 1.
4
Proakis/Salehi/Fundamentals of Communications Systems 2E
© 2014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained
from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical,
photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle
River, NJ 07458.
−5 0 5 10 15 20
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Problem 2.3
x
1
[n] =
1 and
x
2
[n] = cos(
2
πn) =
1, for all
n
. This shows that two signals can be different but
their sampled versions be the same.
Problem 2.4
Let
x
1
[n]
and
x
2
[n]
be two periodic signals with periods
N
1
and
N
2
, respectively, and let
N =
LCM(N
1
, N
2
)
, and define
x[n] = x
1
[n] +x
2
[n]
. Then obviously
x
1
[n +N] = x
1
[n]
and
x
2
[n +N] =
x
2
[n], and hence x[n] = x[n + N], i.e., x[n] is periodic with period N.
For continuous-time signals
x
1
(t)
and
x
2
(t)
with periods
T
1
and
T
2
respectively, in general we
cannot find a
T
such that
T = k
1
T
1
= k
2
T
2
for integers
k
1
and
k
2
. This is obvious for instance if
T
1
=
1 and
T
2
= π
. The necessary and sufficient condition for the sum to be periodic is that
T
1
T
2
be a
rational number.
Problem 2.5
Using the result of problem 2.4 we have:
1.
The frequencies are 2000 and 5500, their ratio (and therefore the ratio of the periods) is
rational, hence the sum is periodic.
2. The frequencies are 2000 and
5500
π
. Their ratio is not rational, hence the sum is not periodic.
3. The sum of two periodic discrete-time signal is periodic.
4.
The fist signal is periodic but
cos[
11000
n]
is not periodic, since there is no
N
such that
cos[11000(n +N)] = cos(11000n) for all n. Therefore the sum cannot be periodic.
5
Proakis/Salehi/Fundamentals of Communications Systems 2E
© 2014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained
from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical,
photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle
River, NJ 07458.

Problem 2.6
1)
x
1
(t) =
e
−t
t > 0
−e
t
t < 0
0 t = 0
=⇒ x
1
(−t) =
−e
−t
t > 0
e
t
t < 0
0 t = 0
= −x
1
(t)
Thus, x
1
(t) is an odd signal
2)
x
2
(t) = cos
120πt +
π
3
is neither even nor odd. We have
cos
120πt +
π
3
= cos
π
3
cos(
120
πt)−
sin
π
3
sin(
120
πt)
. Therefore
x
2e
(t) = cos
π
3
cos(
120
πt)
and
x
2o
(t) = −sin
π
3
sin(
120
πt)
.
(Note: This part can also be considered as a special case of part 7 of this problem)
3)
x
3
(t) = e
−|t|
=⇒ x
3
(−t) = e
−|(−t)|
= e
−|t|
= x
3
(t)
Hence, the signal x
3
(t) is even.
4)
x
4
(t) =
t t ≥ 0
0 t < 0
=⇒ x
4
(−t) =
0 t ≥ 0
−t t < 0
The signal x
4
(t) is neither even nor odd. The even part of the signal is
x
4,e
(t) =
x
4
(t) +x
4
(−t)
2
=
t
2
t ≥ 0
−t
2
t < 0
=
|t|
2
The odd part is
x
4,o
(t) =
x
4
(t) −x
4
(−t)
2
=
t
2
t ≥ 0
t
2
t < 0
=
t
2
5)
x
5
(t) = x
1
(t) −x
2
(t) =⇒ x
5
(−t) = x
1
(−t) −x
2
(−t) = x
1
(t) +x
2
(t)
Clearly
x
5
(−t) ≠ x
5
(t)
since otherwise
x
2
(t) =
0
∀t
. Similarly
x
5
(−t) ≠ −x
5
(t)
since otherwise
x
1
(t) = 0 ∀t. The even and the odd parts of x
5
(t) are given by
x
5,e
(t) =
x
5
(t) +x
5
(−t)
2
= x
1
(t)
x
5,o
(t) =
x
5
(t) −x
5
(−t)
2
= −x
2
(t)
6
Proakis/Salehi/Fundamentals of Communications Systems 2E
© 2014 Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This publication is protected by Copyright and written permission should be obtained
from the publisher prior to any prohibited reproduction, storage in a retrieval system, or transmission in any form or by any means, electronic, mechanical,
photocopying, recording, or likewise. For information regarding permission(s), write to: Rights and Permissions Department, Pearson Education, Inc., Upper Saddle
River, NJ 07458.
剩余598页未读,继续阅读

超威橘猫
- 粉丝: 115
- 资源: 35
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- 27页智慧街道信息化建设综合解决方案.pptx
- 计算机二级Ms-Office选择题汇总.doc
- 单链表的插入和删除实验报告 (2).docx
- 单链表的插入和删除实验报告.pdf
- 物联网智能终端项目设备管理方案.pdf
- 如何打造品牌的模式.doc
- 样式控制与页面布局.pdf
- 武汉理工Java实验报告(二).docx
- 2021线上新品消费趋势报告.pdf
- 第3章 Matlab中的矩阵及其运算.docx
- 基于Web的人力资源管理系统的必要性和可行性.doc
- 基于一阶倒立摆的matlab仿真实验.doc
- 速运公司物流管理模式研究教材
- 大数据与管理.pptx
- 单片机课程设计之步进电机.doc
- 大数据与数据挖掘.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0