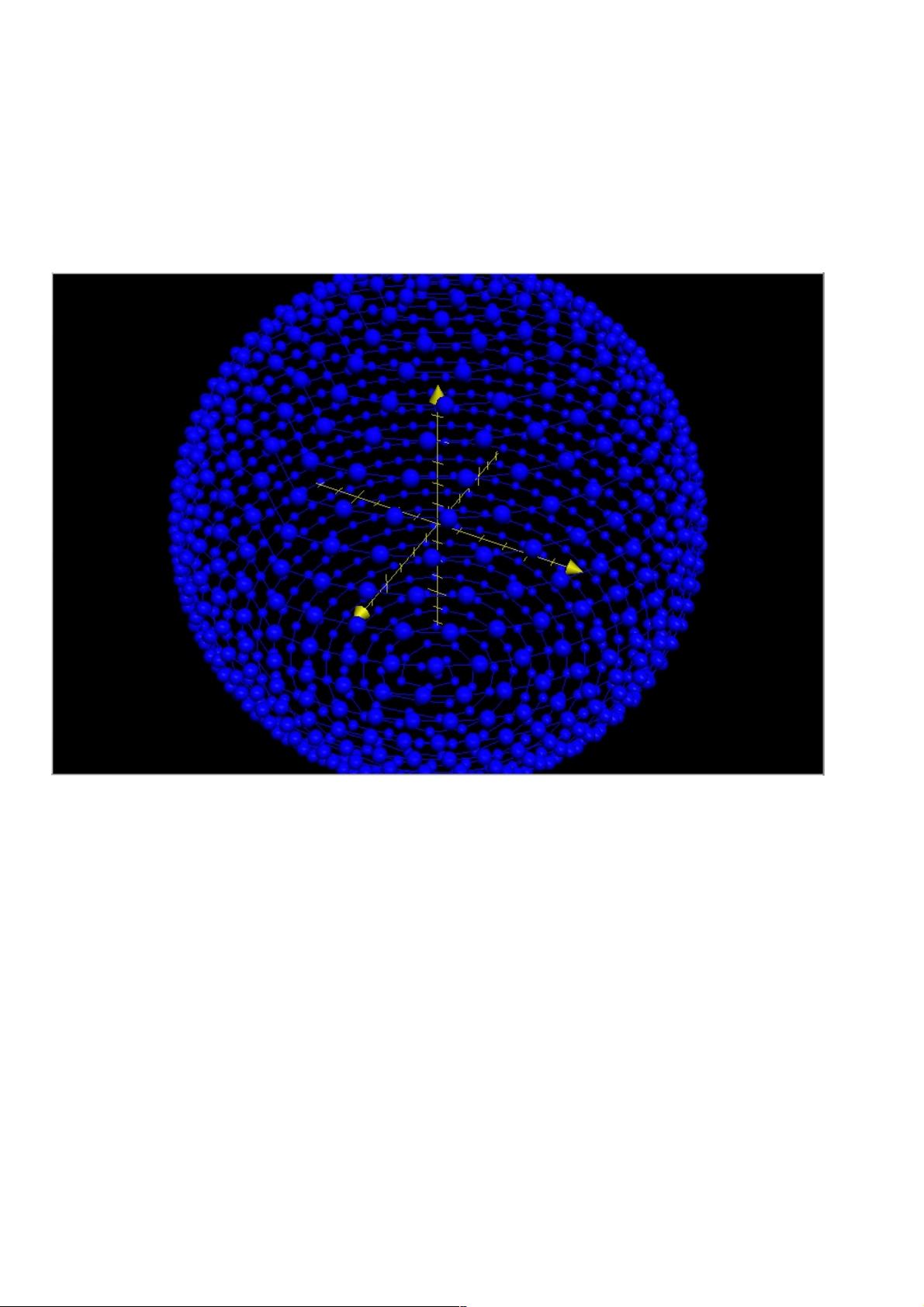
Python实现：均匀分布球面上的n个点

"本文介绍了一种使用Python将n个点均匀分布于球面上的方法，主要通过正八面体剖分策略实现。文章提供了一个名为`sphere.py`的代码示例，该示例创建一个Spherical类来表示球坐标，并通过迭代生成均匀分布的点。" 在Python编程中，有时我们需要在三维空间中模拟物理现象或者进行图形渲染，这时就可能需要将一定数量的点均匀地分布在球面上。本篇文章介绍了一种实用的方法，适合那些在工作中遇到类似需求的开发者参考。 首先，算法的核心思想是利用正多面体的对称性来近似球面。选择正八面体是因为它有八个顶点，每个顶点与其他三个顶点相邻，这使得点的分布相对均匀。通过不断旋转和调整正八面体的各个顶点，可以得到球面上的点。 代码中的`Spherical`类定义了球坐标系统，包含径向（radial）、极角（polar）和方位角（azimuthal）三个参数，并提供了`toCartesian`方法将球坐标转换为直角坐标。这个转换是通过三角函数完成的，例如`x = cos(polar) * r`，其中`r`是径向距离，`polar`是极角，`x`是直角坐标系的x轴坐标。 `splot`函数是实际生成点的主体，它接受一个参数`limit`，表示要生成的点的数量。通过计算，确定了正八面体的剖分方式，即每个方向上的细分步数。`azimuthal`表示方位角的增量，`polar`表示极角的增量。通过双重循环，根据这两个增量逐步生成点的坐标。 最后，程序会根据用户输入的点数调用`splot`函数，然后打印出这些点的直角坐标。这种方法虽然不是严格意义上的完美均匀分布，但对于大量点而言，效果已经相当接近。 通过这篇文章，读者可以了解到如何使用Python结合数学原理来解决实际问题，同时也能学习到Python编程中涉及到的数学函数应用和类的定义。对于想要提升自己在三维空间编程能力的Python开发者来说，这是一个很好的学习资源。