理解SVM：最大间隔与核函数解析

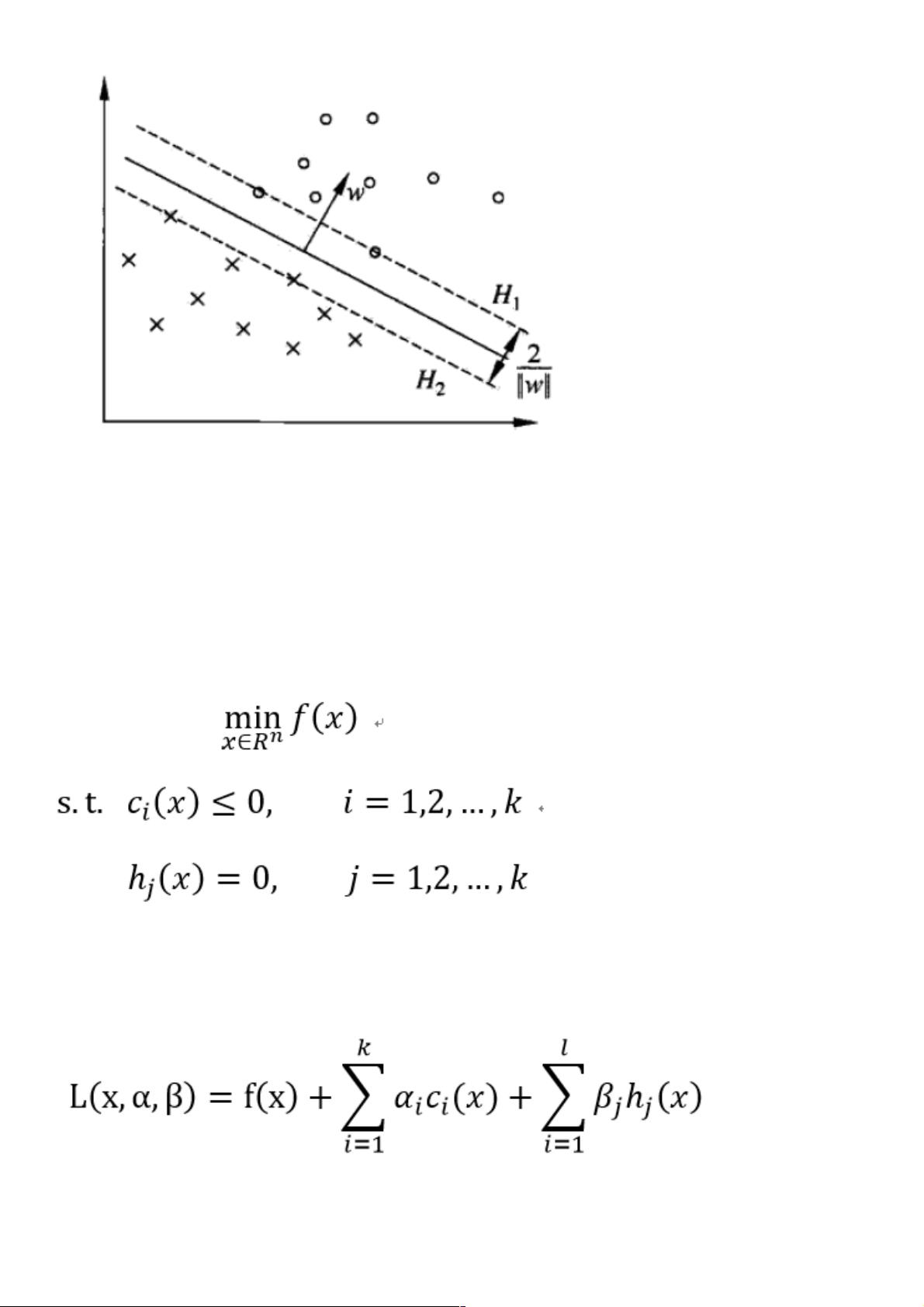
"支持向量机（一）-最大间隔法和核函数" 本文将探讨支持向量机（SVM，Support Vector Machines）这一强大的二分类模型的基本原理。SVM是一种监督学习方法，用于构建分类边界，以最大程度地将不同类别的数据点分开。这个系列笔记分为三部分，本部分主要关注最大间隔法和核函数。 1. 最大间隔法： 支持向量机的核心思想是找到一个最优的决策边界，即最大间隔超平面。这个超平面能够最大化两类样本之间的间隔。间隔定义为从超平面到最近的样本点的距离。在二维平面上，这通常表现为一条直线；在更高维度的空间中，它可以是更复杂的超平面。间隔最大化有助于提高模型的泛化能力，因为它使得模型对训练数据中的噪声和异常值不那么敏感。 为了找到最大间隔超平面，我们可以设置一个线性目标函数，该函数的目标是最小化间隔的逆，同时确保所有样本点都在正确的一侧。对于线性可分的情况，我们可以用硬间隔最大化来实现，即要求所有样本都必须正确分类且位于超平面两侧。然而，如果数据不是线性可分的，就需要引入软间隔最大化，允许一部分样本点可以错误分类，但会受到惩罚。 2. 核函数： 当数据集不是线性可分时，SVM通过引入核函数（Kernel Trick）来解决这一问题。核函数的作用是将原始数据从低维空间映射到高维空间，在高维空间中可能更容易找到一个线性决策边界。常见的核函数有线性核、多项式核、高斯核（RBF）和Sigmoid核。 - 线性核：直接在原始特征空间中计算，适用于线性可分的情况。 - 多项式核：以多项式形式增加特征的交互项，适用于非线性但近似线性的数据。 - 高斯核（RBF）：也称为径向基函数核，以高斯分布的形式计算，适用于非线性且复杂的数据模式。 - Sigmoid核：类似逻辑回归的激活函数，但在高维空间中创建决策边界。 核函数的选择直接影响SVM的性能。选择合适的核函数需要根据数据的特性进行实验和调整，通常可以通过交叉验证来确定最优的核函数和相应的参数。 在实际应用中，我们使用优化算法（如梯度下降或牛顿法）来求解SVM的权重向量w和偏置b，这些值将与选定的核函数一起用于构建分类模型。Matlab等工具提供了实现SVM的库，方便我们进行建模和预测。 支持向量机通过最大间隔法寻找最优分类边界，并通过核函数处理非线性问题，使其在许多机器学习任务中表现出色。理解并熟练应用这两个概念是掌握SVM的关键。