没有合适的资源?快使用搜索试试~ 我知道了~
首页matlab最优化编程方法
matlab最优化编程方法
需积分: 9 9 下载量 67 浏览量
更新于2023-05-20
评论 1
收藏 234KB PDF 举报
本pdf介绍了多种加速matlab计算的方式和方法。从编程的细节到函数的运用以及向量化等等
资源详情
资源评论
资源推荐
DIFFERENTIAL GEOMETRY OF CURVES AND SURFACES
1. Curves in the Plane
1.1. Points, Vec tors, and Their Coordinates. Points and vectors are fundamental
objects in Geometry. The notion of point is intuitive and clear to everyone. The notion
of vector is a bit more delicate. In fa ct, rather than saying what a vector is, we prefer
to say what a vector has , namely: direction, sense, and length (or magnitude). It can be
represented by an arrow, and the main idea is that two arrows represent the same vector if
they have the same direction, sense, and length. An arrow representing a vector has a tail
and a tip. From the (ro ugh) definition a bove, we deduce that in order to represent (if yo u
want, to draw) a given vector as an arrow, it is necessary and sufficient to prescribe its tail.
a a
a
b
bb
c
c
a
P
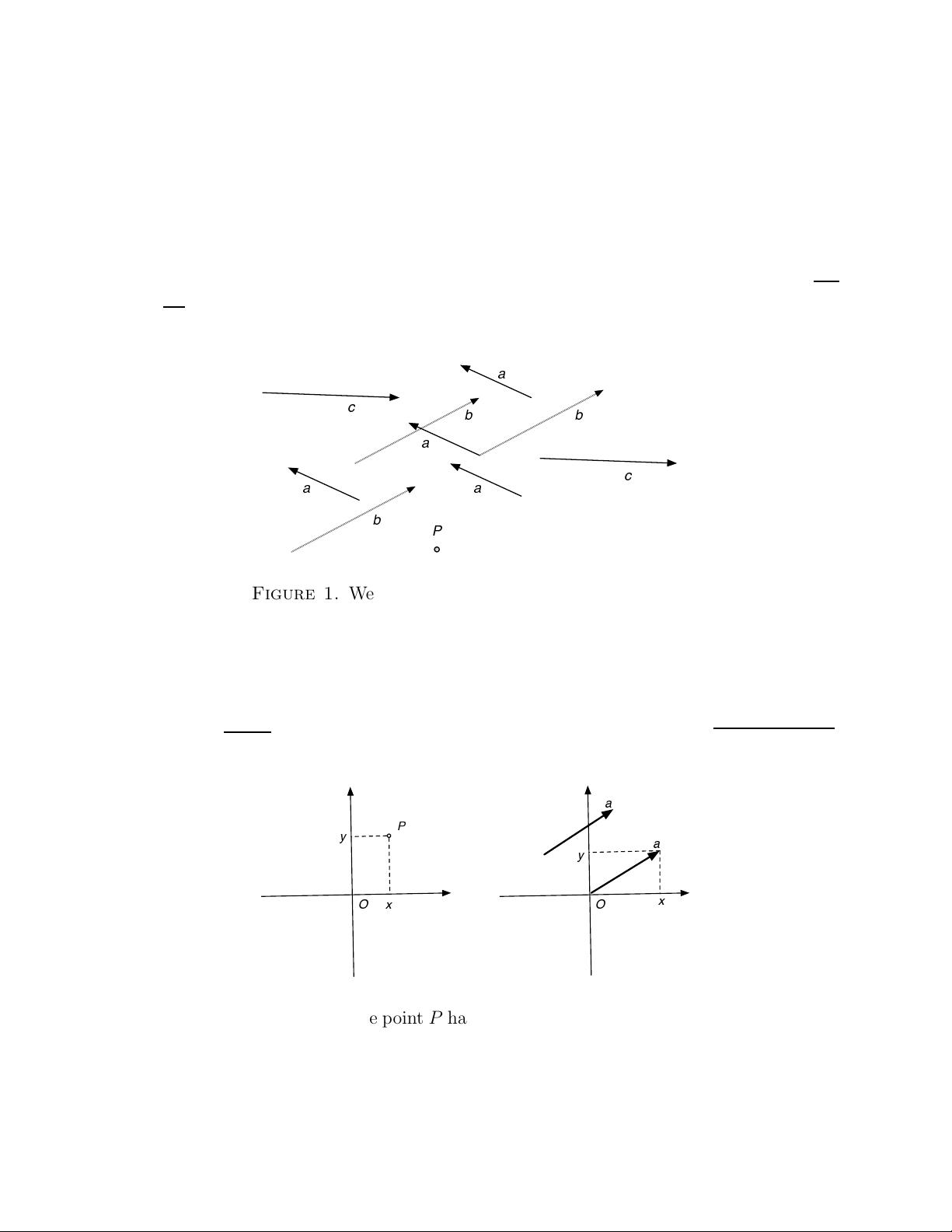
Figure 1. We see four copies of the vector a, three of
the vector b, and two of the vector c. We a lso see a point
P .
An important instrument in handling points, vectors, and (consequently) many other
geometric objects is the Cartesian coordinate system in the plane. This consists of a point
O, called the origin, and two perpendicular lines going through O, called coordinate axes.
Each line has a positive direction, indicated by an arrow (see Figure 2). We denote by R the
O O
P
x
y
x
y
a
a
Figure 2. The point P has coordinates x, y. The vector
a has also coordinates x, y.
set of all real numbers and by R
2
the set of all pairs of numbers, of the form (x, y) , where
x, y are in R. Points are identified with elements R
2
, as follows: to each point P corresponds
the pair (x, y) consisting of the coordinates of the projections of P on the two axes. We say
that P has coordinates (x, y). Also vectors a re identified with elements of R
2
, as follows: if
1

2
a is a vector, we move its tail to the origin O, and we take the coordinates of its tip. We say
that a has coordinates (x, y). One of the first advantag es of the coordinate system is that
we can use it to compute lengths, as follows. The distance between the points P
1
= (x
1
, y
1
)
and P
2
= (x
2
, y
2
) is
kP
1
P
2
k =
p
(x
2
− x
1
)
2
+ (y
2
− y
1
)
2
.
The length of the vector a = (x, y) is
kak =
p
x
2
+ y
2
.
In our course, R
2
will denote both the set of all points and the set of all vectors (in the
plane). It will always be possible to understand from the context if a certain object in R
2
is
a point or a vector.
1.2. Parametrized Curves. A good way of thinking of a curve is as the object which
describes the motion of a particle in the plane: at the time t, the particle is at the point in
the plane whose coordinates are (x(t), y(t)). We stress from the very beginning that what
we are interested in is not simply w h at the trajectory of the particle is, but ra t her how the
trajectory is r un. Now comes the exact definition.
Definition 1.2.1. A parametrized curve in the plane
is a differentiable f unction
1
α(t) = (x(t), y(t)),
where t satisfies a < t < b (possibly a and/or b can be ∞).
When we say that α(t) = (x(t), y(t)) is “differentiable” we mean that both x(t) and y(t)
have derivative of any order (we also say that they are C
∞
differentiable).
The standard notation for such an object is
α : (a, b) → R
2
,
where (a, b) is the open interval between a and b. As we already mentioned, it is importa nt
to distinguish between the curve α (the assignment which associates to any “time” t the
point (x(t), y(t)) on t he “t rajectory”) and the image of the function α (the “trajectory”).
The latter is called the trace
of the curve α.
Remark. Very of t en it is possible to describe the tra ce of a curve α : (a, b) → R
2
with
α(t) = (x(t), y(t)), by an equation of the form f(x, y) = 0, where f is a function of variables
x, y. If so, we say that
x = x(t), y = y(t)
are the parametric equations
(or explicit equations) of the curve and
f(x, y) = 0
is the implicit equation
of the curve. For example, the trace of the curve
x = 1 − 2t, y = 5t
is a straight line (see below). The same line can be describ ed by the implicit equation
5x + 2y = 5.
Also, the circle of radius 1 and centre 0 can be described as the trace of
x = cos t, y = sin t
1
It is worth mentioning that the domain of the function α is the interval a < t < b a nd the range is R
2
.
3
but also by the equation
x
2
+ y
2
= 1.
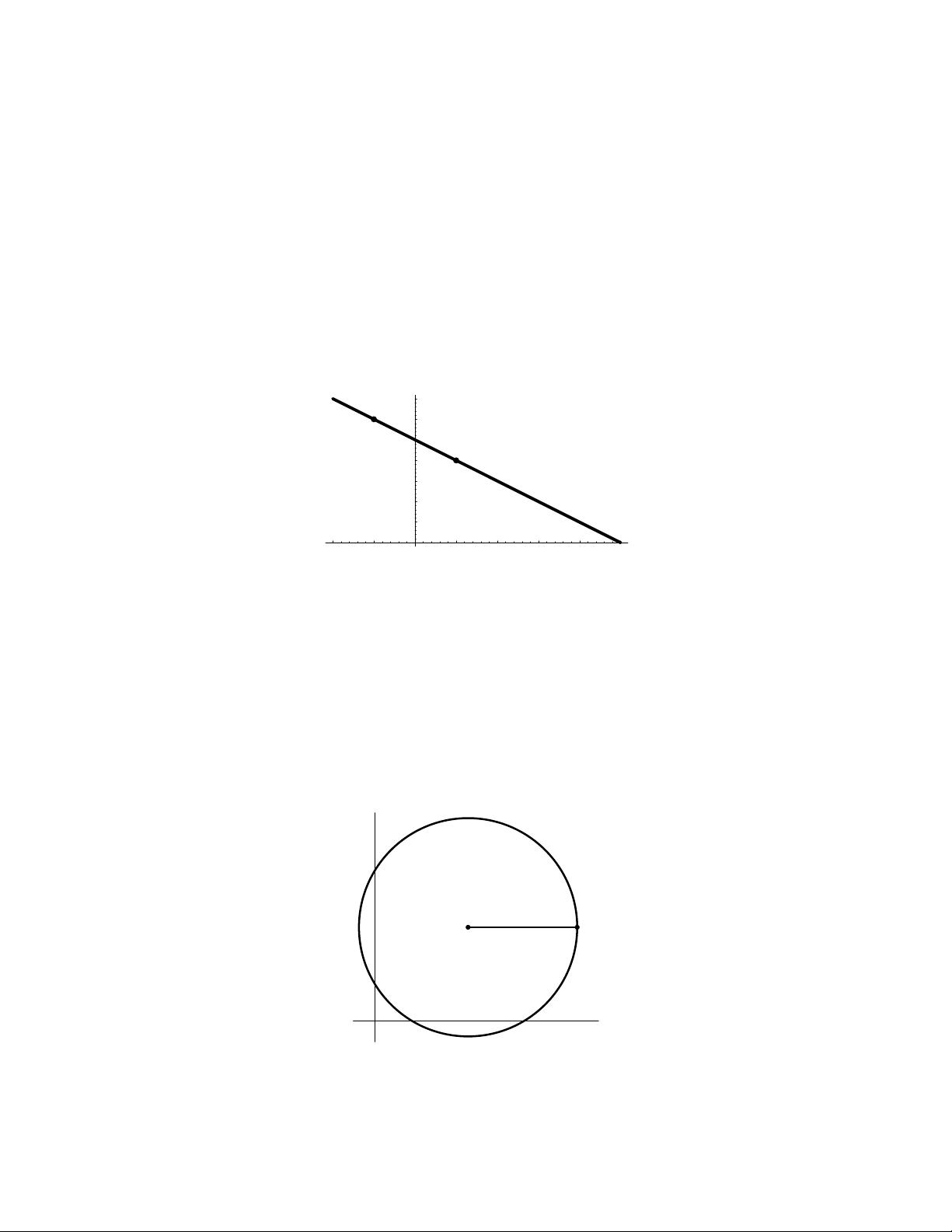
Examples. 1. The straight line determined by two points P and Q is the trace of the curve
α(t) = tP + (1 −t)Q,
where t ∈ R (see Figure 3). Note that there are several other curves whose tr aces are the
same straight line, like for instance
β(t) = tQ + (1 −t)P
or
γ(t) = 2tP + (1 − 2t)Q.
-2
-1 1
2 3
4 5
0.5
1
1.5
2
2.5
3
3.5
Figure 3. The straight line determined by the two in-
dicated points.
2. The circle of center C = (x
0
, y
0
) and ra dius r is the t r ace of the curve
α(t) = (x
0
+ r cos(t), y
0
+ r sin(t)),
for all t in R (see Figure 4). It can be described implicitly as
(x − x
0
)
2
+ (y −y
0
)
2
= r
2
P
C
Figure 4. A circle of center C .
3. The ellipse is the trace of the curve
α(t) = (a cos(t), b sin(t)),
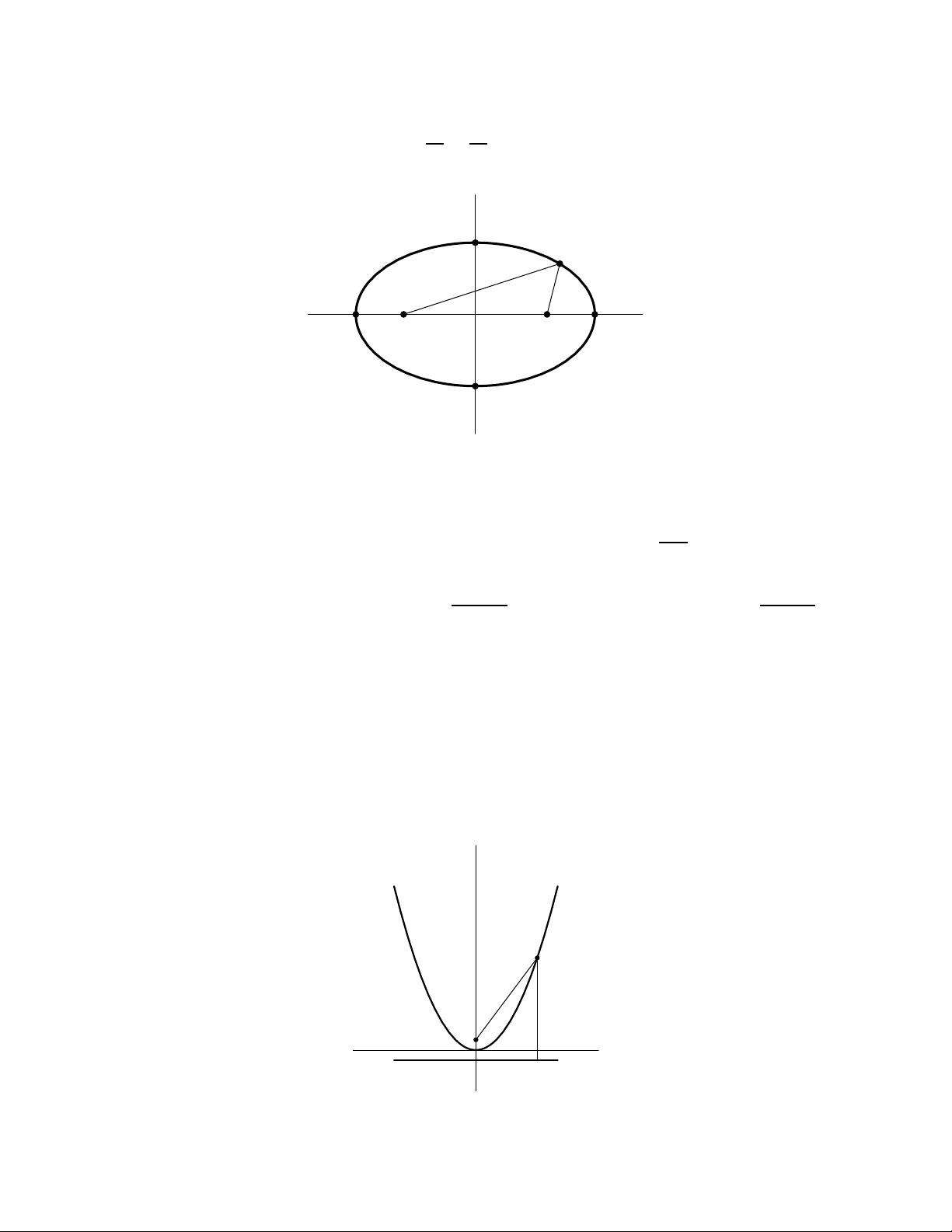
4
for all t in R (see Figure 5). Here a, b are positive numbers. It can be described implicitly as
x
2
a
2
+
y
2
b
2
= 1.
P
F
+
F
-
Ha,0LH-a,0L
H0,bL
H0,-bL
Figure 5. The ellipse with its two foci F
−
and F
+
.
We have the following geometric (coordinate free) characterization of the ellipse. There
exists two points, let’s denote them F
−
and F
+
, which are called the foci
of the ellipse, with
the property that for any point P on the ellipse we have
kP F
−
k + kP F
+
k = constant.
More specifically, F
−
has coordinates (−
√
a
2
− b
2
, 0), and F
+
has coordinates (
√
a
2
− b
2
, 0)
(you are encouraged to calculate the distances k P F
−
k, kP F
+
k, add them up, and check that
the result is constant, that is, independent of t).
4. The parabola is the trace of the curve
α(t) = (t, at
2
),
where a is a number. It can be described implicitly a s
y = ax
2
.
Again we have a geometric (coordinate free) characterization. Namely, there exists a point
P
F
d
Figure 6. The parabola with its focus F and directrix
line d.
剩余19页未读,继续阅读
weixin_43102907
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
收起
我的内容管理
收起
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

会员权益专享
最新资源
- zigbee-cluster-library-specification
- JSBSim Reference Manual
- c++校园超市商品信息管理系统课程设计说明书(含源代码) (2).pdf
- 建筑供配电系统相关课件.pptx
- 企业管理规章制度及管理模式.doc
- vb打开摄像头.doc
- 云计算-可信计算中认证协议改进方案.pdf
- [详细完整版]单片机编程4.ppt
- c语言常用算法.pdf
- c++经典程序代码大全.pdf
- 单片机数字时钟资料.doc
- 11项目管理前沿1.0.pptx
- 基于ssm的“魅力”繁峙宣传网站的设计与实现论文.doc
- 智慧交通综合解决方案.pptx
- 建筑防潮设计-PowerPointPresentati.pptx
- SPC统计过程控制程序.pptx
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功
评论0